Proportionele variatie

Wat is proportionele variatie?

De proportionele variatie tussen twee variabelen "X" en "Y" vindt plaats wanneer, door een van hen met de ene constante te vermenigvuldigen, de andere ook wordt vermenigvuldigd of gedeeld door dezelfde constante. Veel situaties in de echte wereld kunnen met hen correct worden beschreven.

De evenredigheid tussen de variabelen kan direct of omgekeerd zijn. In directe evenredigheid is de relatie van het type:

y = k ∙ x

Of gelijkwaardig:

K = J/X

Waar k een constante wordt genoemd evenredigheid constant of verhouding van evenredigheid. Merk op dat als "x" toeneemt, "y" het in dezelfde verhouding doet, en als "x" afneemt, zal het ook "y". Wanneer de relatie tussen de variabelen grafieken is, wordt een rechte lijn verkregen die door de oorsprong van het coördinatensysteem doorloopt (zie de oefening later opgelost).

De directe variatie kan ook optreden tussen de ene variabele en het ene vermogen van de andere, bijvoorbeeld "Y" kan recht evenredig zijn met X², X³ en dus.

Aan de andere kant zijn de variabelen in omgekeerde evenredigheid gekoppeld door de uitdrukking:

x ∙ y = k

Deze uitdrukking betekent dat het product van de variabelen een constante is. Bij het graferen van de relatie tussen de variabelen is een hyperbool. Als het product van een variabele met de ene kracht van de andere constant is, vertegenwoordigt dit ook een geval van omgekeerde evenredigheid, bijvoorbeeld:

X²∙ y = k; X³∙ y = k ..

Voorbeelden

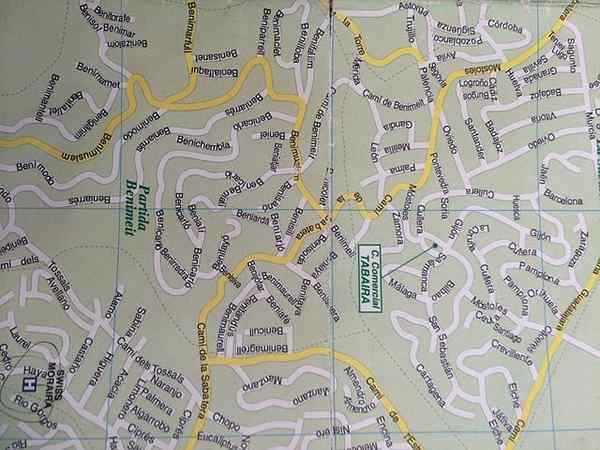Een toepassing van proportionele variatie is kaartenlay -out

Veel wetten van fysica en chemie worden wiskundig uitgedrukt als verhoudingen. De kracht die bijvoorbeeld een veer en de verlenging van hetzelfde uitoefent, de relatie tussen de druk en het volume in een gas bij constante temperatuur, de periode van een eenvoudige slinger en de vierkantswortel van zijn lengte en nog veel meer. Als je het model kent dat het fenomeen regelt, kun je je gedrag achterhalen voor elke waarde van de variabelen.

Kan u van dienst zijn: bestaan ​​en uniekheid Stelling: demonstratie, voorbeelden en oefeningen

En niet alleen dat, ze zijn ook van toepassing in talloze situaties zoals deze:

• Geef het patroon van een kledingstuk van een kleiner formaat door tot een groter formaat (of vice versa).
• In conversiefactoren, om van de ene eenheid naar de andere te gaan, zoals kilometers naar mijlen, gallons naar liters en meer.
• Bereken de ingrediënten van een recept voor 6 mensen die de vereiste voor 4 personen kennen.
• Bepaal het bedrag van bepaalde belastingen in overeenstemming met de verkregen inkomsten.
• In de berekening van eenvoudige rente.
• Bij het opstellen van vliegtuigen.
• Wanneer u de prijs moet berekenen van een aantal producten die de prijs van de eenheid kent.
• In de gelijkenis van driehoeken.

Vervolgens zijn er in detail twee interessante situaties waarin proportionele variaties van toepassing zijn:

voorbeeld 1

Op de schaal van een stad meet de Hermitage Avenue 3.2 cm, zijnde de echte lengte van 400 m. Aan de andere kant moet de straat van La Fuente, die echt 180 m lang meet met een proportioneel kortere slag. Wat is de grootte van de slag?

De verklaring biedt de volledige informatie van de Ermita Avenue: laat de echte lengte van de Avenue en ℓ de lengte op het vlak, omdat de variatie van directe evenredigheid is, moet het:

L = k ∙ ℓ

Uit de gegevens op de Hermitage Avenue kunt u de waarde van de evenredigheidsconstante k kennen, maar voordat het nodig is om alle lengtes in dezelfde eenheden te laten:

3.2 cm = 0.032 m

Dus:

400 m = k ∙ 0.032 m

Daarom is de evenredigheidsconstante:

Kan u van dienst zijn: wat zijn de elementen van de gelijkenis? (Onderdelen)

K = 400/0.032 = 12500

Nu is het bekend dat:

L = 12500 ∙ ℓ

Dit resultaat wordt als volgt geïnterpreteerd: de lengte van de straten op deze kaart is 12500 keer kleiner dan de echte lengte. Daarom meet de lijn van de straat van La Fuente:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44 cm

Voorbeeld 2

Een analist heeft de volgende tabel met waarden voor de variabelen "X" en "Y" experimenteel verkregen en wil weten of deze gegevens passen bij een model van directe proportionele variatie of een van omgekeerde proportionele variatie.

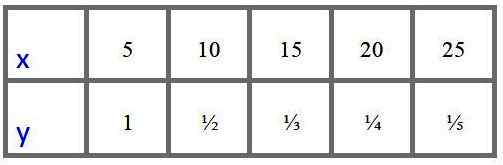
Wat moet u doen om te weten?

In de eerste plaats wordt waargenomen dat wanneer "x" toeneemt, "y" afneemt, dus het vermoedt een omgekeerde evenredigheid, in elk geval, om ervoor te zorgen dat de analist de optie heeft om te beoordelen of het quotiënt en/x constant is (proportioneel variatie direct) of als product x.en is constant (omgekeerde proportionele variatie).

Testen met de eerste optie:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Er wordt geconcludeerd dat het geen directe proportionele variatie is, omdat het quotiënt en/x verschillende waarden geeft voor elk paar gegevens.

We moeten controleren of het product X ∙ constant is:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

En als het product x ∙ y = 5 wordt geconcludeerd dat de variatie van omgekeerde evenredigheid is.

Deze informatie dient om waarden te kennen die niet in de tabel staan, bijvoorbeeld wat de waarde van "y" zou zijn wanneer x = 30?

Van x ∙ y = 5, "y" wordt gewist en vervangen x = 30:

y = 5/x

y = 5/30 = 1/6

Oefening opgelost

Als een stoffenmeter 6 kost.$ 75, en wetende dat de prijs recht evenredig is met het bedrag van de meters om te kopen, zoek:

Het kan u van dienst zijn: antiderivatief: formules en vergelijkingen, voorbeelden, oefeningen

a) De algebraïsche uitdrukking die de variabelen "prijs koppelt aan $" en "Aantal meters stof".

b) Bereid een tabel met waarden voor met prijzen voor 3, 6, 9, 12, 15 en 18 meter stof.

c) Grafiek de verkregen waarden.

Antwoord op

Laat "y" de variabele "prijs voor $" en "x" de variabele "hoeveelheid meters stof". Zoals direct evenredig zijn, moet u:

y = k ∙ x

Voor x = 1 meter, y = 6.$ 75, daarom k = 6.75 $/meter. Dit is de eenheidsprijs van de stof, de prijs van elke andere "x" -stof wordt verkregen door zich te vermenigvuldigen met deze waarde, dan is de gezochte algebraïsche uitdrukking:

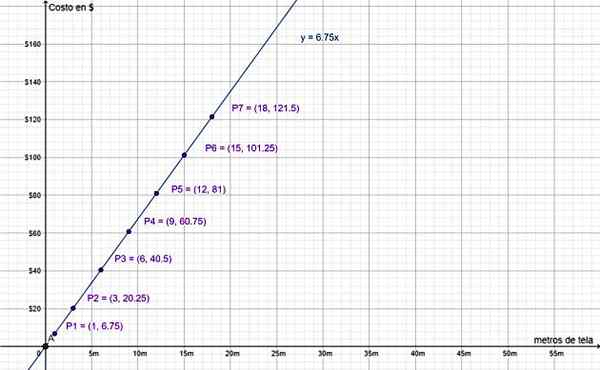
y = 6.75 ∙ x

Antwoord B

De tabel met waarden met prijzen voor $ voor 3, 6, 9, 12, 15 en 18 meter is:

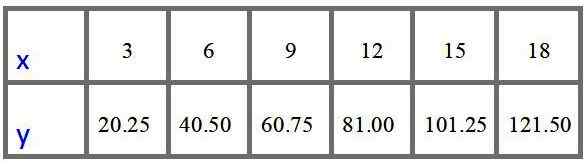
Antwoord C

Ten slotte bevestigt de grafiek van de waarden in de vorige tabel dat het een directe proportionele variatie is:

De kosten voor $ en het bedrag van de stof zijn recht evenredig bedragen. Bron: f. Zapata.

Merk op dat de waarde (0,0) is opgenomen, omdat de regel y = 6.75 ∙ x gaat door de oorsprong van het coördinatensysteem, zoals eerder uitgelegd. Het is logisch, omdat het niet doen van een aankoop gelijk is aan het kopen van 0 m stof, waarvan de waarde 0 $ is.

Referenties

1. Larson, r. 2012. Vóór de sculptuur. 8e. Editie. Cengage leren.
2. Openbaar onderwijs secretariaat van Mexico. De proportionele variatie. Opgehaald uit: PPS.K12.Of.ons.
3. Stewart, J. 2007. Pre-berekening: wiskunde voor berekening. 5e. Editie. Cengage leren.
4. UNAM. Studiegidsen: wiskunde i. Hersteld van: Dirre.UNAM.mx.
5. Zill, D. 2008. Pre-berekening met berekening vooruitgang. 4e. Editie. McGraw Hill.