Continue variabele kenmerken, voorbeelden en oefeningen

De Continue variabele Het is er een die een oneindig aantal numerieke waarden kan nemen tussen twee gegeven waarden, zelfs als die twee waarden willekeurig worden gesloten. Ze worden gebruikt om meetbare attributen te beschrijven; Bijvoorbeeld lengte en gewicht. De waarden die worden genomen door een continue variabele kunnen rationele getallen, reële getallen of complexe getallen zijn, hoewel dit laatste geval minder frequent is in de statistieken. 

Het belangrijkste kenmerk van continue variabelen is dat tussen twee rationele of reële waarden altijd kunnen worden gevonden, en tussen die andere en de eerste kan een andere waarde vinden, en zo voor onbepaalde tijd.

Figuur 1. De curve vertegenwoordigt een continue verdeling en de balken een discreet. Bron: Pixabay

Stel bijvoorbeeld dat de gewichtsvariabele in een groep waar het grootste gewicht 95 kg heeft en het laagste gewicht van 48 kg; Dat zou het bereik van de variabele zijn en het aantal mogelijke waarden is oneindig.

Bijvoorbeeld tussen 50,00 kg en 50,10 kg kan 50.01 zijn. Maar tussen 50,00 en 50.01 kan de maat 50,005 zijn. Dat is een continue variabele. Aan de andere kant, als in de mogelijke gewichtsmaatregelen een enkele decimale nauwkeurigheid werd vastgesteld, zou de gebruikte variabele discreet zijn.

Continue variabelen behoren tot de categorie van kwantitatieve variabelen, omdat ze een numerieke waarde hebben geassocieerd. Met deze numerieke waarde is het mogelijk om wiskundige bewerkingen uit te voeren, variërend van rekenkunde tot de methoden van oneindige berekening. 

[TOC]

Voorbeelden

De meeste variabelen van de fysica zijn continue variabelen, waaronder we kunnen noemen: lengte, tijd, snelheid, versnelling, energie, temperatuur en andere.

Continue variabelen en discrete variabelen

In statistieken kunnen verschillende soorten variabelen worden gedefinieerd, zowel kwalitatief als kwantitatief. Continue variabelen behoren tot deze laatste categorie. Met hen is het mogelijk om reken- en berekeningsactiviteiten uit te voeren.

Bijvoorbeeld de variabele H, overeenkomend met mensen met een hoogte tussen 1,50 m en 1,95 m, is het een continue variabele. 

Laten we deze variabele vergelijken met deze andere: het aantal keren dat duur is bij de lancering van een valuta, die we zullen noemen N.

De variabele N U kunt echter waarden nemen tussen 0 en oneindig N Het is geen continue variabele omdat het de waarde 1,3 of 1,5 niet kan nemen, omdat er tussen waarden 1 en 2 geen andere zijn. Dit is een voorbeeld van Discrete variabele.

Uitoefening van continue variabelen

Overweeg het volgende voorbeeld: een machine produceert fosforwedstrijden en pak ze in de doos. Twee statistische variabelen zijn gedefinieerd:

Kan u van dienst zijn: Isobarisch proces: formules, vergelijkingen, experimenten, oefeningen

Variabele 1: l = ploselengte.

Variabele 2: n = aantal varkens per doos.

De lengte van de nominale overeenkomsten is 5,0 cm met een tolerantie van 0,1 cm. Het aantal varkens per doos is 50 met een tolerantie van 3.

a) Geef het waardenbereik aan dat kan duren L En N.

b) Hoeveel waarden kunt u nemen L?

c) Hoeveel waarden kunt u nemen N?

Zeg in elk geval als het een discrete of continue variabele is.

Oplossing

De waarden van L Ze worden begrepen in het interval [5,0-0,1; 5.0+0.1]; dat wil zeggen dat de waarde van L is in interval [4,9 cm; 5.1 cm] en de variabele L U kunt oneindige waarden nemen tussen deze twee maatregelen. Het is dan een continue variabele.

De waarde van de variabele N is in het interval [47; 53]. De variabele N Het kan slechts 6 mogelijke waarden in het tolerantie -interval nemen, het is dan een discrete variabele.

Uitoefenen van waarschijnlijkheidsverdeling

Als de waarden die door de variabele worden genomen, naast het continu zijn, een bepaalde kans op voorkomen, dan is het een Continue willekeurige variabele. Het is erg belangrijk om te onderscheiden of de variabele discreet of continu is, omdat probabilistische modellen die op elkaar van toepassing zijn, anders zijn.

Een continue willekeurige variabele wordt volledig gedefinieerd wanneer de waarden die ze kunnen veronderstellen bekend zijn, en de kans dat elk van hen moet gebeuren.

-Oefening 1 van waarschijnlijkheden

De matches fabriek maakt ze zodanig dat de lengte van de sticks altijd tussen de 4,9 cm en 5,1 cm waarden ligt, en nul uit deze waarden. Er is de kans om een ​​stok te verkrijgen die tussen 5,00 en 5,05 cm meet, hoewel we ook een van de 5 kunnen extraheren.0003 cm. Zijn deze waarden even waarschijnlijk?.

Kan u van dienst zijn: Relatieve dichtheid: berekening, voorbeelden, oefeningen

Oplossing

Stel dat de kansdichtheid uniform is. Vervolgens worden de kansen op het vinden van een fosfor met een bepaalde lengte vermeld:

-Dat een fosfor in het bereik ligt [4,9; 5,1] heeft waarschijnlijkheid = 1 (of 100%), omdat de machine geen overeenkomsten uit die waarden haalt.

-Het vinden van een fosfor die tussen 4,9 en 5,0 ligt, heeft waarschijnlijkheid = ½ = 0,5 (50%), omdat het de helft van het bereik van de lengtes is.

-En de kans dat de match lengte heeft tussen 5,0 en 5,1 is ook 0,5 (50%)

-Het is bekend dat er geen fosforsticks zijn die een lengte hebben tussen 5,0 en 5,2. Waarschijnlijkheid: nul (0%).

Waarschijnlijkheid om een ​​stok te vinden in een bepaald bereik

Laten we nu de volgende waarschijnlijkheden P waarnemen om sticks te verkrijgen waarvan de lengte tussen L is₁ en ik₂:

 P = (l₂ -l₁) /(L_Maximaal - L_min))

-P dat een match een lengte heeft tussen 5,00 en 5,05 wordt aangeduid als P ([5.00; 5.05]):

P ([5.00; 5.05])) = (5,05 - 5,00)/(5,1 - 4,9) = 0,05/0,2 = ¼ = 0,25 (25%)

-P dat de Cerrillo lengte heeft tussen 5.00 en 5.01 is:

P ([5.00; 5.01])) = (5,00 - 5.01)/(5.1 - 4.9) = 0,01/0,2 = 1/20 = 0,05 (5 %)

-P dat de cerrillo lengte heeft tussen 5.000 en 5.001 is zelfs lager:

P (5.000; 5,001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)

Als we het interval blijven verminderen om meer en meer tot 5,00 te naderen, is de kans dat een stok precies 5,00 cm heeft nul (0%). Wat we wel hebben, is de kans om een ​​match binnen een bepaald bereik te vinden.

Waarschijnlijkheid om verschillende sticks in een bepaald bereik te vinden

Als de gebeurtenissen onafhankelijk zijn, is de kans dat twee sticks zich in een bepaald bereik bevinden het product van hun kansen.

-De kans dat twee sticks tussen 5,0 en 5,1 liggen, is 0,5*0,5 = 0,25 (0,25%)

-De kans dat 50 sticks tussen 5,0 en 5,1 zijn, is (0,5)^50 = 9 × 10^-16, dat wil zeggen bijna nul.

-De kans dat 50 sticks tussen 4,9 en 5.1 zijn, is (1)^50 = 1 (100%)

-Oefening 2 van waarschijnlijkheden

In het vorige voorbeeld werd de veronderstelling gemaakt dat de waarschijnlijkheid uniform is in het gegeven interval, maar het is niet altijd het geval.

Kan u van dienst zijn: Hydrostatische druk: formule, berekening, voorbeelden, oefeningen

In het geval van de echte machine die de sticks produceert, is de mogelijkheid dat de stok zich in de centrale waarde bevindt groter dan in een van de extreme waarden. Vanuit wiskundig oogpunt wordt dit gemodelleerd met een functie F (x) die bekend staat als waarschijnlijkheidsdichtheid.

De waarschijnlijkheid dat de maat is tussen A en B wordt berekend door de gedefinieerde integrale van de functie f (x) tussen a en b. 

Stel bijvoorbeeld dat we de functie f (x) willen vinden, die een uniforme verdeling tussen waarden 4.9 en 5.1 van oefening 1 vertegenwoordigt. 

Als de waarschijnlijkheidsverdeling uniform is, is F (x) gelijk aan constante C, die wordt bepaald dat de integrale tussen 4,9 en 5.1 van C wordt gebruikt. Omdat deze integraal de kans is, moet het resultaat 1 zijn.

Figuur 2. Uniforme waarschijnlijkheidsdichtheid. (Eigen uitwerking)

Wat betekent dat C 1/0,2 = 5 waard is. Met andere woorden, de uniforme waarschijnlijkheidsdichtheidsfunctie is f (x) = 5 als 4.9≤x≤5.1 en 0 uit dit bereik. Figuur 2 toont een uniforme waarschijnlijkheidsdichtheidsfunctie.

Opmerking als in intervallen van dezelfde breedte (bijvoorbeeld 0,02) is de waarschijnlijkheid hetzelfde in het midden als in het einde van het continue variabele bereik L (Augurklengte).

Een realistischer model zou als volgende een waarschijnlijkheidsdichtheidsfunctie zijn:

-f (x) = -750 ((x-5.0)^2-0.01) als 4.9≤x≤5,1

-0 Buiten dit bereik 

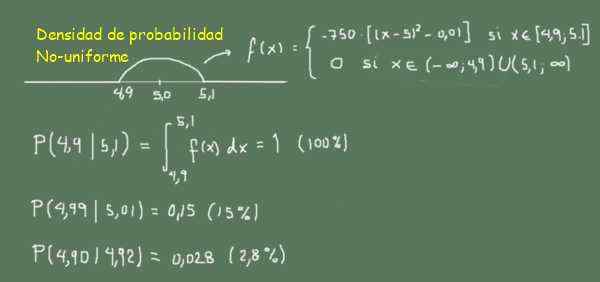figuur 3. Niet -uniforme waarschijnlijkheidsdichtheidsfunctie. (Eigen uitwerking)

In figuur 3 kan het worden waargenomen omdat de kans op het vinden van sticks tussen 4,99 en 5,01 (breedte 0,02) groter is dan het vinden van sticks tussen 4,90 en 4,92 (breedte 0,02)

Referenties

1. Dinov, Ivo. Discrete willekeurige variabelen en waarschijnlijkheidsverdelingen. Hersteld van: stat.UCLA.Edu
2. Discrete en continue willekeurige variabelen. Hersteld van: ocw.MIT.Edu
3. Discrete willekeurige variabelen en waarschijnlijkheidsverdelingen. Hersteld van: homepage.DDMS.Uiowa.Edu
4. H. Peshro. Inleiding tot waarschijnlijkheid. Hersteld van: waarschijnlijkheidscursus.com
5. Mendenhall, W. 1978. Statistieken voor administratie en economie. Ibero -Amerikaanse redactionele groep. 103-106.
6. Willekeurige variabele problemen en waarschijnlijkheidsmodellen. Hersteld van: ugr.is.
7. Wikipedia. Continue variabele. Hersteld van Wikipedia.com
8. Wikipedia. Statistische variabele. Hersteld van Wikipedia.com.