Kenmerken Schuine driehoeken, voorbeelden, oefeningen

De Schuine driehoeken Zij zijn degenen die geen rechte hoek hebben, daarom is geen van hun interne hoeken gelijk aan 90º. Dus een schuine driehoek kan zijn Verbinden of stomp.

In het eerste geval zijn de interne hoeken van de driehoek acuut of wat hetzelfde is: minder dan 90º, terwijl in de tweede altijd een hoek groter is dan 90º, dat wil zeggen een stompe hoek. Laten we eens kijken naar een voorbeeld van elk in de volgende figuur:

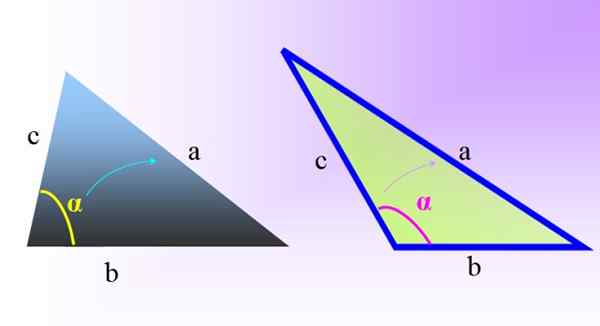Figuur 1. Schuine driehoeken: aan de linkerkant een schuine en acutangle -driehoek. Rechts een schuine en stompe driehoek. Bron: f. Zapata.

Om de lengtes van de zijkanten en de metingen van de interne hoeken van dit soort driehoeken te vinden, is het in afwezigheid van rechte hoeken niet mogelijk om de stelling van Pythagoras toe te passen.

Er zijn echter alternatieven om de driehoek op te lossen: de stellingen van de cosinus en de boezem en het feit dat de som van de interne hoeken gelijk is aan 180º.

[TOC]

Oblicuágulos Triangles Voorbeelden

Door onszelf te leiden door figuur 1, kunnen we de schuine driehoeken gemakkelijk herkennen door twee criteria die we hieronder zullen geven.

Acutangle -driehoek

Wees de driehoek van zijden A, B en C, met α de hoek voor de zijkant.

Als het vierkant aan de zijkant tegenover de acute hoek α, minder is dan de som van de vierkanten van de resterende zijkanten, is de driehoek acutangle. Algebraïsch:

naar² < b² + C²; α < 90º

De relatieve gelijkzijdige driehoek, degene die zijn drie zijden van dezelfde maat heeft, is acutangle en daarom schuin, omdat de interne hoeken gelijk zijn en 60º meten.

Stompe driehoek

Aan de andere kant, als het vierkant aan de andere kant naar Bij de stompe hoek α is groter dan de som van de vierkanten van de andere twee, we zijn in aanwezigheid van een stompe driehoek. Daarom:

naar² > B² + C²; α> 90º

Een driehoek waarvan de interne hoeken bijvoorbeeld 105º, 60º en 15º zijn, is een stompe schuine driehoek. Merk op dat 105º + 60º + 15º = 180º.

Stelling van de sinus en cosinus

Om de schuine driehoeken op te lossen, dat wil zeggen om de maatregelen van al hun zijden en al hun hoeken te vinden, zijn de stellingen van de borst en de cosinus vereist.

Laat A, B en C de zijkanten van een driehoek en α, β en γ hun interne hoeken. Dus:

Borststelling

De stelling van de borst stelt het volgende vast:

Waar α de tegenovergestelde hoek voor zij A is, is β de hoek tegenover zijde B en γ is de hoek voor zij C.

Het kan u van dienst zijn: antiderivatief: formules en vergelijkingen, voorbeelden, oefeningen

Equivalent:

We kiezen ervoor om de borststelling toe te passen wanneer we een driehoek gaan oplossen dan meer hoeken bekend zijn dan partijen.

Coseno Stelling

Volgens de stelling van Coseno:

C² = A² + B² - 2⋅a⋅b⋅cos γ

Opnieuw staat de hoek γ voor zijkant C. We kunnen ook equivalente uitdrukkingen schrijven voor zijden A en B, als volgt:

naar² = B² + C² - 2⋅b⋅c⋅cos α

EN

B² = A² + C² - 2⋅a⋅c⋅cos β

De cosinus -stelling wordt bij voorkeur toegepast wanneer de waarde van twee zijden en de hoek ertussen bekend is. Ook, zodra de drie zijden van een driehoek bekend zijn, stelt de stelling ons in staat om de cosinus van de hoek tussen twee te berekenen.

Opgeloste oefeningen

- Oefening 1

Controleer of de driehoek waarvan de zijden 20, 10 en 12 willekeurige eenheden meten, stompe is.

Oplossing

We kennen geen van de interne hoeken, maar volgens de criteria die dienen om stompe driehoeken te herkennen, kunnen we ongelijkheden verhogen met de vierkanten van de partijen om te observeren of deze wordt vervuld.

Eerst vinden we de vierkanten aan elke kant:

twintig² = 400

10² = 100

12² = 144

En we zien dat inderdaad: 400> 100 + 144, sinds 400> 244. Daarom bevat de driehoek een hoek groter dan 90º, gelegen voor de zijkant die 20 meet. Bijgevolg is deze driehoek, naast schuin, ook stompe.

- Oefening 2

Gezien de schuine driehoek getoond in figuur 2, waarvan de maatregelen worden gegeven in willekeurige eenheden, bepaalt u:

a) De waarde van x. Is het een acutangle of stompe driehoek?

b) De resterende interne hoeken van de driehoek

c) perimeter

d) gebied.

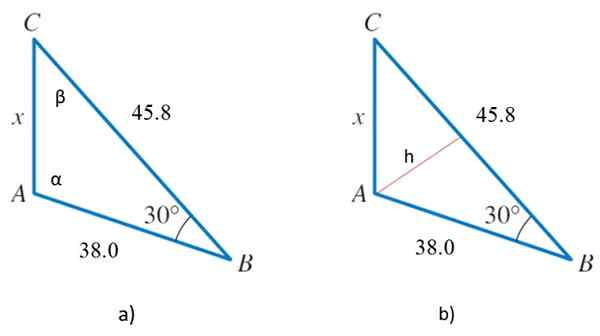Figuur 2. 2a) driehoek voor het jaar loste 2 en 2b op) dezelfde driehoek met een hoogte, die zal dienen om het gebied te bepalen. Bron: f. Zapata.

Oplossing voor

Van de driehoek zijn twee aangrenzende zijden bekend, waarvan de maatregelen 38 zijn.0 en 45.8 en de hoek ertussen, die 30º is, daarom wordt de cosinus -stelling onmiddellijk toegepast:

X² = 38.0² + Vier vijf.8² - 2 x 38.0 x 45.8 x cos 30º = 527.18

Daarom:

x = (527.18)^1/2 = 22.96

De tekening suggereert dat α> 90º en de driehoek stompe is, naast schuine. Om het te controleren, vinden we de vierkanten van de zijkanten, zoals in de vorige oefening werd gedaan:

22.96² = 527.18

38.0² = 1444.00

Vier vijf.8² = 2097.64

De hoek α is groter dan 90º als het waar is dan het vierkant van de andere kant: 45.8²  Het is groter dan de som van de vierkanten van de andere zijden, die 22 is.96² + 38.0².

Kan u van dienst zijn: wetten van exponenten

Laten we kijken of het gebeurt:

527.18 + 1444.00 = 1971.2

Inderdaad:

2097.64> 1971.2

Daarom is de hoek α groter dan 90º.

Oplossing B

Nu kunnen we de borststelling toepassen om een ​​van de ontbrekende hoeken te vinden. We gaan het verhogen voor hoek β:

Sen 30º / 22.96 = sin β / 38

Sen β = 38 x (Sen 30º / 22.96) = 0.8275

β = arcsen (0.8275) = 55.84º

De ontbrekende hoek kan worden gevonden, wetende dat de som van de interne hoeken van elke driehoek 180º is. Daarom:

55.84º + 30º + α = 180º

α = 94.16º

Indien voorkeur, kunt u ook de cosinus -stelling gebruiken om de cosinus te vinden van de hoek die tussen twee aangrenzende kanten ligt. Zodra de Coseno -boogfunctie wordt gebruikt om de hoek te bepalen.

De resultaten kunnen een beetje verschillen in de decimalen, volgens de uitgevoerd afronding.

Oplossing C

De omtrek P is de contour van de figuur, equivalent aan de som van de metingen van de drie zijden:

P = 22.96 + 38.00 + 45.80 = 106.76 willekeurige eenheden.

Oplossing D

De formule om het gebied van een driehoek te berekenen is:

A = (1/2) x Basis x Hoogte

We moeten als basis een van de zijkanten kiezen en de hoogte bepalen. Bijvoorbeeld het kiezen van de kant die 45 meet.8, we tekenen de hoogte H tot vertex A, de rode lijn in figuur 2b.

Door dit te doen verdelen we de oorspronkelijke driehoek in twee rechthoeken, beide met H Als een gemeenschappelijke cateto. Elk van hen dient, omdat we een scherpe kant en hoek kennen.

We gaan degene die Hypotenusa heeft gelijk aan 38 nemen, een categorie die meet H, die de gezochte hoogte is en de acute hoek gelijk aan 30º.

Met behulp van de trigonometrische redenen van de acute hoek 30º bepalen we de waarde van H:

Sen 30º = cateto tegenover 30º / hypotenusa = h / 38

H = 38 x Sen 30º = 19

Daarom:

A = (1/2) x 45.8 x 19 = 435.1 willekeurige gebiedsgebieden.

We hadden een andere kant als basis kunnen kiezen, bijvoorbeeld zijde 38, in dat geval de hoogte H Het is anders, omdat een andere rechthoekige driehoek wordt gevormd, maar het resultaat van het gebied is hetzelfde. Het blijft als oefening voor de lezer om het te controleren.

- Oefening 3

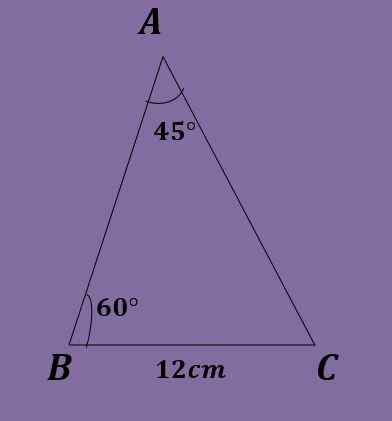
Gegeven een ABC -driehoek die a = 45º, b = 60º en a = 12 cm, bereken de andere driehoekgegevens.

Kan u van dienst zijn: tekenen van groepering

Oplossing

Met behulp van dat is de som van de interne hoeken van een driehoek gelijk aan 180º het moet:

C = 180º-45º-60º = 75º.

De drie hoeken zijn al bekend. Dan gaan we verder met het gebruik van de borstwetgeving om de twee kanten te berekenen die ontbreken.

De vergelijkingen die zich voordoen, zijn 12 / zonder (45º) = b / zonder (60º) = C / zonder (75º).

Uit de eerste gelijkheid kunt u "B" wissen en dat verkrijgen:

b = 12*zonder (60º)/zonder (45º) = 6√6 ≈ 14.696 cm.

U kunt ook "C" wissen en dat krijgen:

C = 12*sin (75º)/sin (45º) = 6 (1+√3) ≈ 16.392 cm.

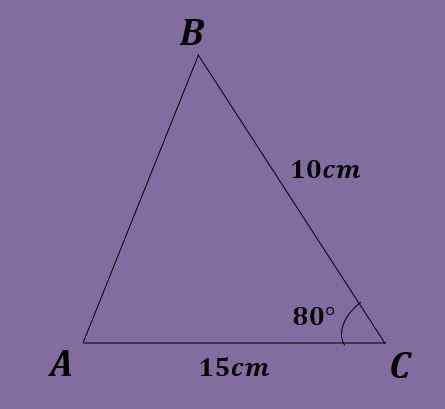
- Oefening 4

Gegeven de driehoek ABC zodanig dat a = 60º, C = 75º en B = 10 cm, de andere driehoekgegevens berekenen.

Oplossing

Zoals in het voorgaande jaar moet je b = 180º-60º-75º = 45º = 45º moeten. Bovendien moet u met behulp van de borstwetgeving / zonder (60º) = 10 / zonder (45º) = c / zonder (75º), waar wordt verkregen dat a = 10*zonder (60º) / zonder (45º) = 5 √6 ≈ 12.247 cm en c = 10*sin (75º)/zonder (45º) = 5 (1+√3) ≈ 13.660 cm.

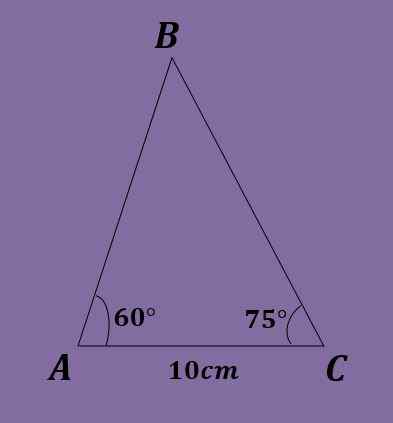
- Oefening 5

Gegeven de driehoek ABC zodanig dat a = 10 cm, b = 15 cm en c = 80º, bereken de andere driehoekgegevens.

Oplossing

In deze oefening is alleen een hoek bekend, daarom is het niet mogelijk om te beginnen zoals deze werd gedaan in de twee vorige oefeningen. Bovendien kan de borstwetgeving niet worden toegepast omdat er geen vergelijking kan worden opgelost.

Daarom wordt de wet van Cosenos toegepast. Je moet:

C² = 10²+15² - 2 (10) (15) cos (80º) = 325 - 300*0.173 ≈ 272.905 cm,

Zodat C ≈ 16.51 cm. Nu, wetende de 3 zijden, wordt de borstwetgeving gebruikt en wordt verkregen dat:

10 / zonder (a) = 15 / zonder (b) = 16.51 cm /zonder (80º).

Vanaf hier, wanneer Clear B zonder (b) = 15*zonder (80º)/ 16 is.51 ≈ 0.894, wat inhoudt dat B ≈ 63.38º.

Nu kan worden verkregen dat a = 180º - 80º - 63.38º ≈ 36.62º.

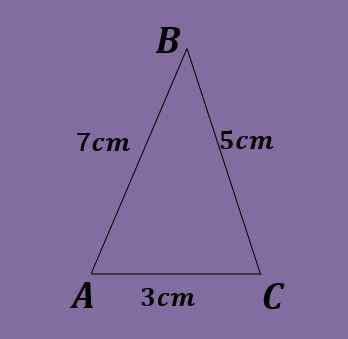
- Oefening 6

De zijkanten van een schuine driehoek zijn a = 5 cm, b = 3 cm en c = 7 cm. Bereken de hoeken van de driehoek.

Oplossing

Nogmaals, de borstwetgeving kan niet direct worden toegepast, omdat geen vergelijking zou dienen om de waarde van de hoeken te verkrijgen.

Met behulp van de wet van de cosinus moet u c² = a² + b² - 2ab cos (c), van waar cos (c) = (a² + b² - c²)/ 2ab = (5² + 3² -7²)/ 2*5 *3 = -15/30 = -1/2 en daarom C = 120º.

Nu kan de borstwetgeving worden toegepast en dus 5/zonder (a) = 3/zonder (b) = 7/zonder (120º) verkrijgen, waarbij B kan worden gewist b en die zonder (b) = 3* zonder (120º verkrijgen (120º )/7 = 0.371, zodat B = 21.79º.

Eindelijk wordt de laatste hoek berekend met die A = 180º-130º-21.79º = 38.21e.

Referenties

1. Clemens, s. Geometrie met toepassingen. Addison Wesley.
2. Ibáñez, p. 2010. Wiskunde III. Cengage leren.
3. Jiménez, r. Wiskunde II: Geometrie en trigonometrie. 2e. Editie. Pearson.
4. Wiskunde voor jou. Stompe driehoek. Hersteld van: wiskunde voor.WordPress.com.
5. Stewart, J. 2007. Voorzetting. 5e. Editie. Cengage leren.