Stompe driehoek

We leggen uit wat een stompe driehoek is, de elementen, kenmerken, typen, voorbeelden en een opgeloste oefening

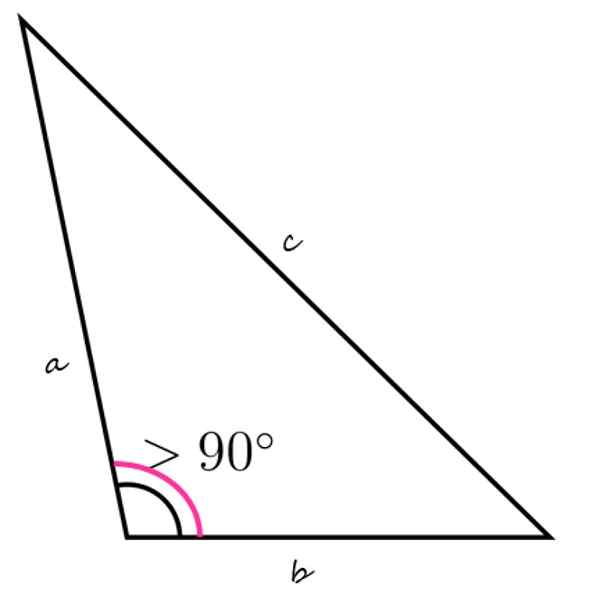De stompe driehoek wordt gekenmerkt door een interne hoek groter dan 90º te hebben

Wat is een stompe driehoek?

A stompe driehoek Het is de platte figuur, gesloten en met drie zijden, die ook een stompe interne hoek bevat, dat wil zeggen groter dan 90º en minder dan 180º.

Elke driehoek bevat 3 interne hoeken, en als een van hen stompe is, zijn de andere twee, door geweld, acuut, omdat de som van de interne hoeken van een driehoek altijd gelijk is aan 180º.

De bovenste figuur toont een voorbeeld van een stompe driehoek, met de interne hoek linksonder groter dan 90º. De resterende interne hoeken moeten minder dan 90º toevoegen, alleen op deze manier is het waar dat de som van de drie gelijk is aan 180º.

Naast de stompe driehoeken zijn er acutangeuze driehoeken, als al zijn interne hoeken acuut zijn en rechthoekige driehoeken, wanneer een van de interne hoeken precies 90º meet.

Elementen van de stompe driehoeken

Obtusángulos -driehoeken hebben de gemeenschappelijke elementen voor alle driehoeken: het zijn 3 -zijdige vlakke figuren, met 3 interne hoeken en 3 hoekpunten. Bovendien hebben ze opmerkelijke segmenten, genaamd Cevians, zoals hoogte, mediaan en mediatrix, en punten waar Cevians elkaar kruisen.

Elk van deze elementen is kort gedefinieerd als volgt:

-Zijkanten, zijn de segmenten die de figuur vormen.

-Hoekpunten, kruispunten van elk paar aangrenzende kanten.

-Interne hoeken, Ze zijn tussen twee aangrenzende zijden, aan de binnenkant van de figuur, samenvallen van het hoekpunt van de hoek met die van de driehoek.

-Externe hoeken, Ze zijn tussen één kant en de uitbreiding van de aangrenzende zijde, buiten de figuur, het hoekpunt is gebruikelijk, zowel van de driehoek als de hoek. De som van de maatregel tussen de interne hoek en de externe aangrenzende hoek is 180º, zodat ze complementaire hoeken zijn.

Het kan u van dienst zijn: Tukey -test: wat is, in het geval van bijvoorbeeld, opgeloste oefening

-Hoogte, Het is de maat van het loodrechte segment dat zich bij een hoekpunt met de andere kant verbindt, of met de uitbreiding hiervan.

-Mediaan, lijn die wordt gericht vanaf een hoekpunt naar het midden van de andere kant.

-Middelares, segment loodrecht op de zijkant en dat passeert net door het midden.

-Bissectrice, Het is een segment dat zich in een halve interne hoek van de driehoek verdeelt.

-Orocentro, kruispunt van de drie hoogten.

-Barycenter, Ook wel Centroid genoemd, het is het punt waar de drie mediaan elkaar kruisen.

-Circumcentro, Hier zijn de drie mediatrices gesneden.

-In het midden, samenvloeiingspunt van bissectors.

Zodra deze concepten zijn beoordeeld, worden enkele van de meest opvallende kenmerken van de stompe driehoeken hieronder beschreven.

Kenmerken

1.- De som van de drie interne hoeken van de stompe driehoek is 180º, daarom kan slechts één van de interne hoeken groter zijn dan 90º, terwijl de som van de resterende twee minder is dan 90º is.

2.- De langste kant van de stompe driehoek is tegen de stompe hoek.

3.- In een stompe driehoek kruisen de hoogten van de hoekpunten die acute hoek maken.

4.- De orthocenter van een stompe driehoek is uit de figuur.

5.- De circumcentro van de stompe driehoek valt ook uit de driehoek (dit gebeurt niet met de Acutangle -driehoek).

6.- Het is alleen mogelijk om een ​​vierkant in de stompe driehoek te registreren, ter ondersteuning van een van de zijkanten van het vierkant aan de langste kant van de driehoek. Twee vierkanten kunnen worden getrokken en ondersteunen de zijkant aan de kortste zijden van de driehoek, waardoor een hoekpunt niet is geregistreerd (waardoor de zijkant van de driehoek niet raakt).

Kan u van dienst zijn: Tidecágono

7.- Wees een stompe driehoek van zijkanten (a, b, c), als C de langste zijde. De volgende ongelijkheid is geldig:

naar²+B² < c²

8.- Het zijn twee stompe driehoeken, waarvan de respectieve zijden zijn (A, B, C) en (U, V, W). De langste zijden van elk zijn C en W, dus de volgende ongelijkheid wordt vervuld:

A ∙ U + B ∙ V < c∙w

Soorten belemmerende driehoeken

De stompe driehoeken kunnen van twee soorten zijn, volgens de lengte van hun zijden:

• Gelijkbenig
• Scaleen

Ze worden hieronder kort beschreven:

Gelijkbenige driehoek

Het is er een die twee gelijke kanten heeft en een andere, dat wil zeggen, zijn zijden zijn (a, a, c).

Wanneer de gelijkbenige driehoek beide stompe is, zijn de zijkanten van meet "A" korter en is de "C" -zijde de langste. De stompe hoek wordt gevormd tussen dezelfde zijden, terwijl de twee acute hoeken van gelijke mate zijn en worden gevormd tussen zijkanten "A" en de zijde "C".

En zoals vermeld in het voorgaande gedeelte, zijde "C", omdat het de langste is, is het tegen de stompe hoek.

Ongelijkbenige driehoek

De drie zijden van de Scaleense driehoek hebben verschillende maatregel: (a, b, c).

Voorbeelden

voorbeeld 1

De driehoek die in de volgende figuur wordt getoond, is stom. De stompe hoek is γ = 114.5e en het is geverifieerd dat de som van de drie interne hoeken 180º is:

114.5e + 36.8º + 28.6e ≈ 180º

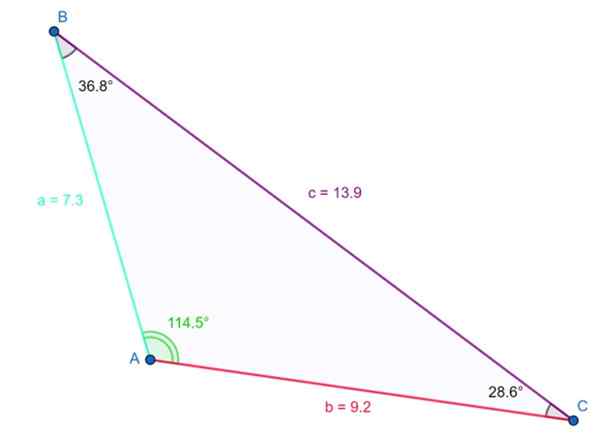Voorbeeld van stompe driehoek. Bron: f. Zapata

De langste kant meet 13.9 eenheden en is tegen de stompe hoek. Aan de bovengenoemde ongelijkheid wordt ook voldaan:

naar²+B² < c²

Kan u van dienst zijn: evenredigheidsrelaties: concept, voorbeelden en oefeningen

JA A = 7.3 en B = 9.2, dan:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Voorbeeld 2

In de Calabi -driehoek is het mogelijk om het grootst mogelijke vierkant, op drie verschillende manieren in de driehoek te plaatsen, zoals weergegeven in de volgende figuur.

Calabi's driehoek is gelijkbenig en stompe. De stompe hoek is ongeveer 101.736 ° en acute hoeken aan de basis meet beide 39.13e, ook ongeveer.

Oefening opgelost

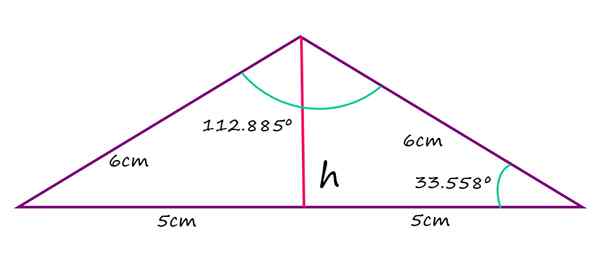
De gelijke zijden van een stompe gelijkbenige driehoek maatregel 6 cm, terwijl de langste zijde 10 cm meet. Bereken de waarde van de stompe hoek, die van de resterende Agudos -hoeken en de hoogte van genoemde hoekpunt naar de basis.

Oplossing

De cosinus -stelling kan worden gebruikt om de cosinus van de stompe hoek te vinden. Vervolgens wordt met behulp van de rekenmachine de kwestie in kwestie bepaald, aangeduid als γ.

De stelling van Coseno stelt dat:

C² = a² +B² - 2ab ∙ cos γ

Waarbij γ de hoek is tussen zijden A en B. Omdat de driehoek gelijkbenig is, zijn zijkanten A en B daarom hetzelfde:

C² = 2a² - 2e²∙ cos γ

Cos γ opruimen:

 De stompe hoek is de -0 cosinusboog.38889, dat is ongeveer 112.885º. De waarde van α, de acute hoek gevormd door de 6 cm zijden met de 10 cm is:

2a + 112.885º = 180º

α = (180 - 112.885)/2 = 33.558º

Gelijkbenige stompe driehoek. Bron: f. Zapata

Wat betreft de hoogte van de driehoek, gemeten vanaf de basis, wordt verkregen door op te merken dat deze hoogte de driehoek verdeelt in twee gelijke rechthoeken, met hypotenusa gelijk aan 6 cm en basis 5 cm. In een dergelijk geval is de Pythagoras -stelling van toepassing om direct de waarde van H te vinden: