Trapecio Issmeteigenschappen, relaties en formules, voorbeelden

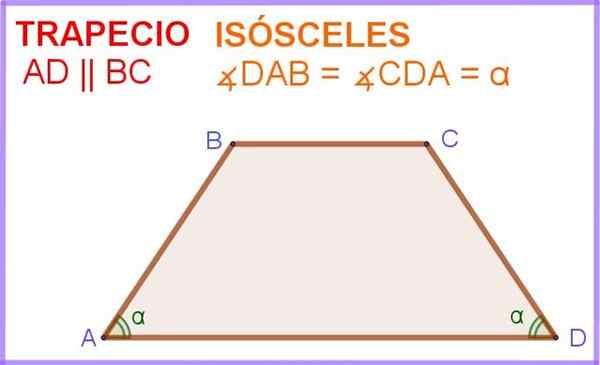
A trapeze gelijkbenig Het is een vierhoek waarin twee van de zijkanten parallel aan elkaar zijn en ook de twee hoeken grenzend aan een van die parallelle zijden hebben dezelfde maatregel.

In figuur 1 heb je de ABCD -vierhoek, waarin de advertentie- en BC -zijden parallel zijn. Bovendien hebben de hoeken ∠dab en ∠ADC naast de parallelle zij -advertentie dezelfde maat α. 

Figuur 1. Trapezium eisosceles. Bron: f. Zapata.

Aldus is deze vierhoek of vierzijdige polygoon in feite een gelijkbenige trapezoid.

In een trapeze worden de parallelle zijden genoemd honken en niet-parallellen worden genoemd zijdelings. Een ander belangrijk kenmerk is het hoogte, dat is de afstand die de parallelle kanten scheidt.

Naast de gelijkbenige trapezoid zijn er andere soorten trapeze:

-TRapecio escaleno, dat heeft al zijn verschillende invalshoeken en kanten.

-TRechthoek rapecio, waarin een kant recht aangrenzende hoeken heeft.

De trapeziumvormige vorm komt vaak voor in verschillende ontwerpgebieden, architectuur, elektronica, berekening en nog veel meer, zoals later zal worden gezien. Vandaar het belang om vertrouwd te raken met zijn eigenschappen.

[TOC]

Eigenschappen

Exclusieve gelijkbenige trapezoid

Als een trapeze gelijkbenig is, voldoet dan aan de volgende karakteristieke eigenschappen:

1.- De zijkanten hebben dezelfde maatregel.

2.- De hoeken grenzend aan de bases zijn hetzelfde.

3.- Tegengestelde hoeken zijn aanvullend.

4.- De diagonalen hebben dezelfde lengte, hetzelfde zijn de twee segmenten die de tegenovergestelde hoekpunten verenigen.

5.- De hoek gevormd tussen de basen en de diagonalen is allemaal van dezelfde maatregel.

6.- Het heeft een omschreven omtrek.

Wederzijds, als een trapeze aan een van de vorige eigenschappen voldoet, is het een gelijkbenige trapezoid.

Als in een trapezoid gelijkbenig is, is een van de hoeken recht (90º), dan zullen alle andere hoeken ook zijn, waardoor een rechthoek wordt gevormd. Dat wil zeggen, een rechthoek is een bepaald geval van gelijkbenige trapezoid.

Figuur 2. De Corn Palomites -container en schooltafels zijn de vorm van gelijkbenige. Bron: Pxfuel (links)/McDowell Craig door Flickr. (rechts)

Voor alle trapezoid

De volgende set eigenschappen is geldig voor elke trapeze:

7.- De mediaan van de trapeze, dat is het segment dat zich bij de middelpunten van zijn niet -parallelle zijden verbindt, is parallel aan een van de bases.

8.- De lengte van de mediaan is gelijk aan de semi -semum (som gedeeld door 2) van die van zijn bases.

9.- De mediaan van een trapezium snijdt zijn diagonalen in het middelpunt.

10.- De diagonalen van een trapeze kruisen elkaar op een punt dat ze in twee secties verdelen die evenredig zijn aan de quotiënten van de basen.

elf.- De som van de vierkanten van de diagonalen van een trapeze is gelijk aan de som van de vierkanten van zijn zijkanten plus het dubbele product van zijn bases.

Het kan je van dienst zijn: hoeveel duizendste passen ze in een tiende?

12.- Het segment dat zich bij de middendiagonale punten verbindt, heeft lengte gelijk aan de semi -verwijzing van de bases.

13.- De hoeken grenzend aan de zijkanten zijn aanvullend.

14.- Een trapeze heeft een geregistreerde omtrek als en alleen als de som van zijn bases gelijk is aan de som van zijn zijkanten.

vijftien.- Als een trapeze een geregistreerde omtrek heeft, dan zijn de hoeken met hoekpunt in het midden van genoemde omtrek en zijkanten die door de uiteinden van dezelfde kant gaan, rechtstreeks hoeken.

Relaties en formules

De volgende reeks relaties en formules worden verwezen naar figuur 3, waar naast de reeds genoemde trapezoi van de gelijkbenige trapezoid, zoals diagonalen, hoogte en medium.

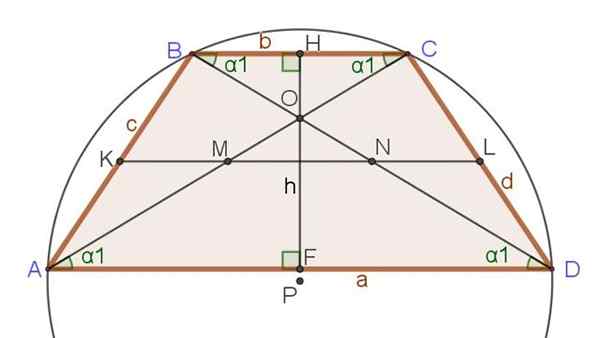figuur 3. Mediane, diagonalen, hoogte en omtrek omschreven in een kloppende trapezoid. Bron: f. Zapata.

Exclusieve relaties van de gelijkbenige Trapecio

1.- AB = DC = C = D

2.- ∡dab = ∡cda en ∡abc = ∡bcd

3.- ∡dab + ∡bcd = 180º en ∡cda + ∡abc = 180º

4.- BD = AC

5.- ∡cad = ∡bda = ∡cbd = ∡bca = α₁

6.- A, B, C en D behoren tot de omschreven omtrek.

Relaties voor elke trapezoid

7. Als AK = KB en DL = LC ⇒ KL || AD en KL || BC

8.- Kl = (AD + BC)/2

9.- AM = MC = AC/2 en DN = NB = DB/2

10.- AO/OC = AD/BC Y DO/OB = AD/BC

elf.- AC² + Db² = AB² + DC² + 2⋅ad⋅bc

12.- Mn = (AD - BC)/2

13.- ∡DAB + ∡ABC = 180º en ∡CDA + ∡BCD = 180º

14.- Als AD + BC = AB + DC ⇒ ∃ r wat equidista van AD, BC, AB en DC

vijftien.- Als ∃ r wat equidista van AD, BC, AB en DC, dan:

∡bra = ∡drc = 90º

Issmeles trapezoid relaties met geregistreerde omtrek

Als in een gelijkbenige trapezium de som van de basen gelijk is aan de dubbele van een zijde, dan is er de geregistreerde omtrek.

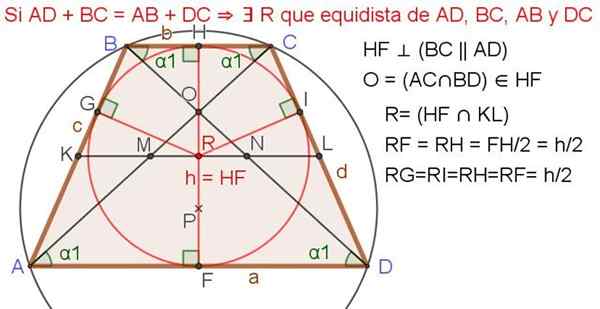Figuur 4. Trapeze met geregistreerde omtrek. Bron: f. Zapata.

De volgende eigenschappen zijn van toepassing wanneer het gelijkbenige trapezoid een geregistreerde omtrek heeft (zie figuur 4 hierboven):

16.- Kl = AB = DC = (AD + BC)/2

17.- De diagonalen worden onder de rechterkant gesneden: AC ⊥ BD

18.- De hoogte is hetzelfde als de mediaan: hf = kl, dat wil zeggen h = m.

19.- Het vierkant van de hoogte is gelijk aan het product van de bases: h² = BC⋅AD

twintig.- Onder deze specifieke omstandigheden is het trapeze -gebied gelijk aan het kwadraat van de hoogte of het product van de bases: gebied = h² = BC⋅AD.

Formules om de ene kant te bepalen, de anderen en een hoek bekend

Bekende één basis, de zijkant en een hoek, de andere basis kan worden bepaald door:

a = b + 2c cos α

B = a - 2c cos α

Als de lengte van de basen bekend staat als bekend en een hoek, dan is de lengtes van beide zijden:

Het kan u van dienst zijn: Fermat Limit: wat bestaat en oefeningen opgelost

C = (a - b) / (2 cos α)

Vastberadenheid aan de ene kant, bekend de anderen en een diagonaal

A = (D₁² - C²)/ B;

B = (D₁² - C²)/ naar 

C = √ (D₁² - A⋅B)

Waar D₁ Het is de lengte van de diagonalen.

Basis vanaf de hoogte, het gebied en de andere basis

a = (2 a)/h - b

b = (2 a)/h - a

Bekend terug de bases, het gebied en een hoek

C = (2a) /[(a + b) sin α]

Bekend lateraal de mediaan, het gebied en een hoek

C = a / (m.sin α)

Bekende hoogte de zijkanten

H = √ [4 c² - (A - b)²]

Bekende hoogte een hoek en twee kanten

H = Tg α⋅ (a - b)/2 = c . sin α

Bekende diagonalen alle kanten, of twee kanten en een hoek

D₁ = √ (c²+ A B)

D₁ = √ (a²+ C² - 2 a c cos α)

D₁ = √ (b² + C²- 2 b c cos β)

Gelijkbenige driehoekig perimeter 

P = a + b + 2c

Gelijkbenig trapeziumgebied

Er zijn verschillende formules om het gebied te berekenen, afhankelijk van de bekend gegevens. Het volgende is de bekendste, afhankelijk van de bases en hoogte:

A = H⋅ (A + B)/2

En deze anderen kunnen ook worden gebruikt:

-Als de zijkanten bekend zijn

A = [(a +b)/4] √ [4c² - (A - b)²]

-Als je twee kanten en een hoek hebt

A = (B + C cos α) C Sen α = (a - c cos α) c sen α

-Als de straal van de geregistreerde omtrek bekend is en een hoek

A = 4 r² / Sin α = 4 r² / Sin β

-Wanneer de bases en een hoek bekend zijn

A = a⋅b / sin α = a⋅b / sen β 

-Als de trapeze een omtrek kan worden geregistreerd

A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b)/2

-Bekend de diagonalen en hoek die zich met elkaar vormen

A = (D₁²/2) sen γ = (D₁² / 2) sen δ 

-Als je de zijkant hebt, de mediaan en een hoek

A = MC.sin α = mc.Sen β

Omschreven omtrekradio

Alleen Issmeles trapezoïden hebben een omschreven omtrek. Als de hoofdbasis bekend is, is de zij C en de diagonale D₁, Dan is de straal R van de omtrek die door de vier hoekpunten van de trapeze passeert:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p -d₁)]

Waar p = (a + c + d₁) / 2

Voorbeelden van het gebruik van de gelijkbenige trapezoid

Het gelijkbenige trapezoid verschijnt in het ontwerpveld, zoals te zien in figuur 2. En hier hebben we enkele aanvullende voorbeelden:

In architectuur en constructie

De oude Inca's kenden de gelijkbenige trapezoid en gebruikten het als een constructie -element in dit venster van Cuzco, Peru:

Figuur 5 . Venster met een trapeziumvormige vorm van de Coricancha, cuzco. Bron: Wikimedia Commons.

En hier verschijnt het trapezoid opnieuw in de oproep Trapeziumvormige blad, Een vaak gebruikt materiaal in constructie:

Figuur 6. Trapeziumvormige metalen plaat die de ramen van een gebouw tijdelijk beschermt. Bron: Wikimedia Commons.

In ontwerp

We hebben al gezien dat de gelijkbenige trapezoid verschijnt in alledaagse voorwerpen, inclusief voedsel zoals deze chocoladereep:

Figuur 7. Chocoladereep waarvan de gezichten de vorm hebben van gelijkbenige. Bron: PxFuel.

Opgeloste oefeningen

- Oefening 1

Een gelijkbenige trapezoid is gebaseerd dan 9 cm, base minder dan 3 cm en zijn diagonalen elk 8 cm. Berekenen:

Het kan u van dienst zijn: algemene parabola -vergelijking (voorbeelden en oefeningen)

A) ZIJ

b) hoogte

c) perimeter

d) ärea

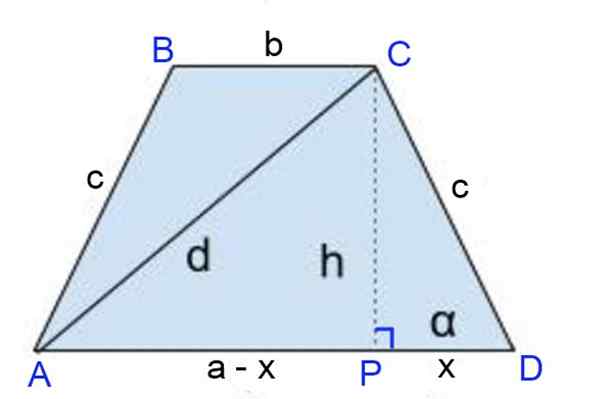Figuur 8. Schema voor oefening 1. Bron: f. Zapata

Oplossing voor

De hoogte CP = H wordt getekend, waarbij de voet van de hoogte de segmenten definieert:

Pd = x = (a-b)/2 en 

Ap = a - x = a - a/2 + b/2 = (a + b)/2.

Door de stelling van Pythagoras naar de DPC -rechthoekige driehoek:

C² = h² + (A - b)² /4

En ook naar de APC -rechthoekige driehoek:

D² = h² + AP² = h² + (A+B)² /4

Ten slotte wordt een lid afgetrokken, de tweede vergelijking van de eerste en vereenvoudigt:

D² - C² = ¼ [(a+b)² - (A-B)²] = ¼ [(a+b+a-b) (a+b-a+b)]]

D² - C² = ¼ [2a 2b] = a b

C²= D² - A B ⇒ C = √ (D² - a b) = √ (8² - 9⋅3) = √37 = 6,08 cm

Oplossing B

H² = D² - (A+B)² /4 = 8² - (12² / 2² ) = 8² - 6² = 28

H = 2 √7 = 5,29 cm

Oplossing C

Perimeter = a + b + 2 c = 9 + 3 + 2⋅6,083 = 24,166 cm

Oplossing D

Gebied = h (a+b)/2 = 5,29 (12)/2 = 31,74 cm

- Oefening 2

Er is een gelijkbenige trapezoid waarvan de grootste basis twee keer zo klein is en de kleinste basis is gelijk aan de hoogte, die 6 cm is. Bepalen:

a) de zijkant van de zijkant

b) perimeter

c) gebied

d) hoeken

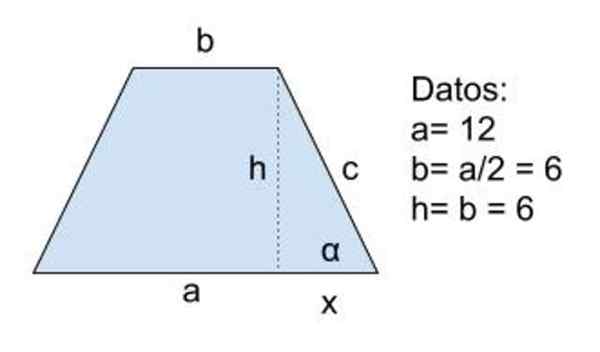Figuur 8. Schema voor oefening 2. Bron: f. Zapata

Oplossing voor

Gegevens: a = 12, b = a/2 = 6 en h = b = 6

We gaan op deze manier verder: de hoogte H is getekend en de Pythagoras -stelling wordt toegepast op de hypotenuse -driehoek "C" en Catetos H en X:

C² = h²+XC²

Vervolgens moet u de hoogtewaarde berekenen uit de gegevens (h = b) en de cateto x: 

a = b + 2 x ⇒ x = (a-b)/2

De vorige uitdrukkingen vervangen die u hebt:

C² = B²+(A-B)²/2²

Nu worden numerieke waarden geïntroduceerd en vereenvoudigd:

C² = 62+ (12-6) 2/4

C² = 62 (1+¼) = 62 (5/4)

Het verkrijgen van:

C = 3√5 = 6,71 cm

Oplossing B

De perimeter P = A + B + 2 C

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Oplossing C

Het gebied op basis van de hoogte en lengte van de bases is:

A = H⋅ (A + B)/2 = 6⋅ (12 + 6)/2 = 54 cm²

Oplossing D

De hoek α die de zijde vormt met de hoofdbasis wordt verkregen door trigonometrie:

Tan (α) = h / x = 6/3 = 2

α = arctan (2) = 63,44º

De andere hoek, die de zijde vormt met de kleine basis is β, die aanvullend is voor α:

β = 180º - α = 180º - 63.44º = 116,56º

Referenties

1. EN. NAAR. 2003. Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
2. Campos, f. 2014. Wiskunde 2. Patria -redactiegroep.
3. Vrijgelaten, k. 2007. Ontdek polygonen. Benchmark -onderwijsbedrijf.
4. Hendrik, V. 2013. Gegeneraliseerde polygonen. Birkhäuser.
5. Iger. Wiskunde eerste semester Tacaná. Iger.
6. Jr. Geometrie. 2014. Polygonen. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. 2006. Wiskunde: redeneren en applicaties. 10e.  Editie. Pearson Education.
8. Patiño, m. 2006. Wiskunde 5. Redactionele progreso.
9. Wikipedia. Trapeze. Hersteld van: is.Wikipedia.com