Lineaire transformaties eigenschappen, wat zijn het gebruik, typen, voorbeelden

A Lineaire transformatie, die we gewoon zullen aanroepen, relateert de elementen van twee vectorruimtes V en W, waarbij elke vector wordt toegewezen v behorend tot V een enkele vector W die tot W behoort, via een specifieke bewerking.

Deze transformatie voldoet aan twee voorwaarden:

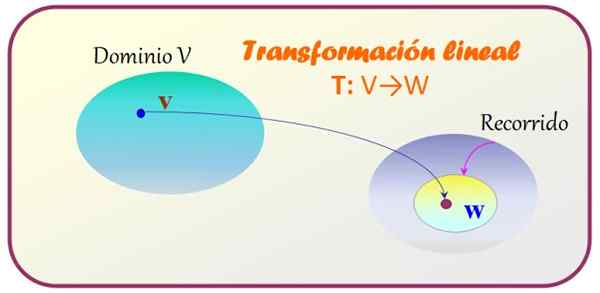
Figuur 1. Een lineaire transformatie is van toepassing op een vector van vectorruimte V om een ​​andere vector te verkrijgen die tot de W -vectorruimte behoort. Bron: f. Zapata.

-Voorwaarde 1

Het verwijst naar de toevoeging, zodat een t -lineaire transformatie moet worden vervuld die:

T (v + W) = T (v) + T (W))

-Voorwaarde 2

De tweede voorwaarde vertegenwoordigt homogeniteit in de vermenigvuldiging van een scalaire door een vector:

T (cv) = c⋅t (v))

De lineaire transformatie, zoals de naam al aangeeft, is verantwoordelijk voor het in kaart brengen of transformeren van elementen van V in elementen van W.

De notatie voor functies wordt ook gebruikt in het geval van lineaire transformaties, dus het domein van V is de set elementen (vectoren) die moeten worden getransformeerd, terwijl het codominium of route de resulterende set is.

Een voorbeeld van lineaire transformatie is:

Om aan te geven dat de letter T zal worden gebruikt. De transformatie zal op een vector worden toegepast v wiens componenten X en Y zijn, die is weergegeven door een enkele kolommatrix. Het resultaat is een andere vector W wiens componenten x en 0 zijn, ook weergegeven door een kolommatrix.

Daarom is dit een transformatie van de R -vectorruimte R² Naar de vectorruimte r², dat het samengevat is geschreven als volgt:

T: r² → R²         

Als we de vector hebben:

De transformatie keert ons terug:

En dus met elke R -vector². In Voorbeeld 1 wordt geverifieerd dat deze transformatie lineair is.

[TOC]

Eigenschappen van lineaire transformaties

Stel dat een lineaire transformatie van V in W, in welke vectoren v En of Ze behoren tot V, dan worden aan de volgende eigenschappen bereikt:

Eigendom 1

T (0) = 0

Waar 0 is de nulvector.

Eigendom 2

T (-v) = - t (v))

Eigendom 3

T (of  - v) = T (of) - T (v))

Eigendom 4

Zijn v = c₁v₁ + C₂v₂ +.. . +  C_Nv_N

 Dus:

T (c₁v₁ + C₂v₂ +.. . +  C_Nv_N) = C₁ T (v₁) + c₂ T (v₂) +.. . +  C_N T (v_N))

Elementen van lineaire transformatie

Laat V en W al vectorruimtes vermelden waar de lineaire transformatie T elementen van V transformeert naar w. We kunnen de volgende elementen definiëren:

-C Nucleus of kernel: Het is een subset van het domein waaraan het wordt aangeduid door N (t) of ker (t) en begrijp alle elementen van V zodanig dat:

T (v) = 0.

De lineaire transformatie t (v) = 0 wordt genoemd Null -transformatie.

Natuurlijk de nulvector v = 0 Vervult hoe dan ook met deze voorwaarde, maar de kernel bestaat uit de hele niet -nul vectoren die het ook vervullen, voor een gegeven T.

Kan u van dienst zijn: GROTE FUNCTIE: Hoe u het kunt identificeren, voorbeelden, oefeningen

-Afbeelding van t: Het is de set vectoren die tot W behoren, zodat het beeld van ten minste een vector in V is. Het wordt aangeduid als Im t) En het is subset van de W vectorruimte.

Deze elementen zullen ons helpen lineaire transformaties later te classificeren.

Waar zijn lineaire transformaties voor?

Aanvankelijk werken lineaire transformaties met vectorruimtes, gevormd door vectoren. Vaak associëren we vectoren met sterkte en andere fysieke magnitudes, maar bij digitale beeldverwerking kan een pixel worden weergegeven door een vector.

In dat geval kan de afbeelding worden gemanipuleerd door handige lineaire transformaties om de gewenste effecten te verkrijgen, bijvoorbeeld projecteren, roteren, het spiegelbeeld vinden of de grootte wijzigen zonder de relatieve afmetingen te wijzigen.

Lineaire transformaties worden ook veel gebruikt in economie en besluitvorming, bijvoorbeeld om de hoeveelheid grondstof te kennen die nodig is om een ​​bepaalde productbatch te produceren.

Het aantal stukken dat nodig is om de verschillende modellen te assembleren die door een fabriek zijn geproduceerd, kan worden bewerkt door een matrixopstelling, zoals we later zullen zien.

Soorten lineaire transformaties (classificatie)

Net als functies kunnen lineaire transformaties zijn:

-Injectief of monomorfismen

-Bijectieven of Epimorfismen

-Overjectief of Isomorfismen

Bovendien zijn de volgende typen:

-Endomorfismen

-Automorfismen.

Injectieve lineaire transformaties

Laat V- en W -vectorruimtes en t een lineaire transformatie t: V → W. T is injectief wanneer:

Kerel (T) = 0

Lineaire overjectieve transformaties

Als V en W de vectorruimtes zijn zodat t: v → w, wordt gezegd dat t bijectief is wanneer:

Im (t) = w

Bijjectieve lineaire transformaties

Een lineaire transformatie T: V → W is bijectief wanneer het zowel injectief als overjectief is. Daarom is het vervuld dat:

Kerel (T) = 0 En Im (t) = w

Endomorfismen

Het zijn lineaire transformaties waarin domein en codominium samenvallen.

Automorfismen

Dit soort lineaire transformaties zijn bijectieve endomorfismen.

Speciale lineaire transformaties

Lineaire operator

Een lineaire transformatie T: V → V, die van een vectorruimte naar dezelfde vectorruimte gaat, wordt genoemd Lineaire operator.

Nul -transformatie

Hierboven vermeld is nultransformatie belangrijk om de kernel van een lineaire transformatie te vinden:

Het kan u van dienst zijn: Tetradecágon

T: v → W zodanig dat t (v) = 0 Voor enige v.

Identiteitstransformatie

T: v → V zodanig dat t (v) = v  Voor enige v.

Transformatie gedefinieerd door een matrix

T: v → W zodanig dat t (v) = Av, waar a een matrix is ​​en v Het is een kolomvector.

Lineaire functie

De lineaire functies van het Y = MX -type zijn lineaire transformaties. Neem bijvoorbeeld Y = 3x en kijk of het voldoet aan de twee voorwaarden van het begin, testen met twee waarden A en B Any:

f (a+b) = 3 (a+b) = 3a+3b = f (a)+f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

Het is inderdaad een lineaire transformatie.

Toepassingen

Lineaire transformaties hebben wiskundige toepassingen, zoals:

-Coördinaat assen rotatie.

-In de oplossing van systemen van lineaire differentiaalvergelijkingen.

-Zelfwaarde- en autovery -problemen.

En ze hebben ook toepassingen op andere wetenschapsgebieden, bijvoorbeeld in mechanica, kwantummechanica en economie, onder andere gebieden.

Voorbeelden van lineaire transformaties

voorbeeld 1

In veel mechanische problemen moeten we de projectie van een vector vinden v behoren tot de ruimte, op een bepaald vlak. Deze vector v kan bijvoorbeeld een kracht vertegenwoordigen.

Stel dat u de vector wilt projecteren v = Op het xy -vliegtuig. We kunnen een lineaire transformatie definiëren die wordt gegeven door de volgende matrix:

Wanneer we het op de vector toepassen v We krijgen een vector waarvan de Z -component is geannuleerd. Geometrisch wordt het weergegeven, met de projectie van v Op het XY -vlak als de rode vector met twee componenten.

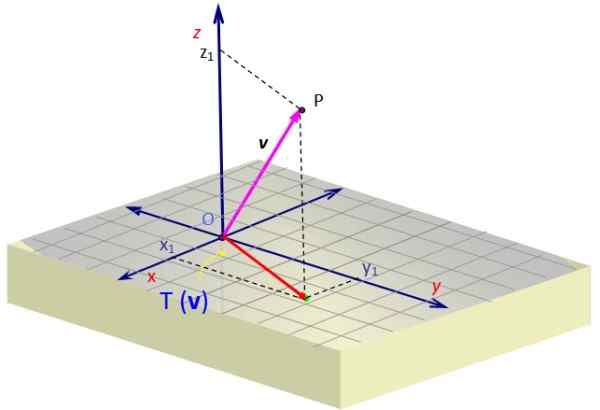Figuur 2. Projectie van een vector in de ruimte op een vlak, dat wordt verkregen door een lineaire transformatie. Bron: f. Zapata.

Voorbeeld 2

Stel dat u een fabriek hebt die drie soorten speelgoedkarren produceert: C1, C2 en C3, waarvoor u op zijn beurt drie soorten stukken in bepaalde hoeveelheden nodig heeft om elk type kar te produceren:

-Bijlen of stuk

-Wielen of stuk B

-Chassis of stuk c

Voor elk type kar is het aantal stukken anders, omdat de modellen verschillend zijn. We kunnen de hoeveelheden in een 3 × 3 -matrix bevatten, waarin de kolommen worden geleid door het type kar, en de rangen komen overeen met de hoeveelheid stukken die nodig zijn om elk model uit te werken.

Dit is een voorbeeld van transformatie gegeven door een matrix die zo zou zijn:

Als de fabriek een bepaalde inkooporder ontvangt, die uit bestaat uit X hoeveelheid C1, En  van C2 en Z Van C3, hoeveel stukken A, B en C moeten beschikbaar zijn om de bestelkarren te monteren?

Het kan u van dienst zijn: wat zijn algebraïsche uitdrukkingen en welke zijn de meest voorkomende?

We moeten een lineaire transformatie t (x) vinden zodat:

Om de vector te krijgen en:

Dat geeft ons de hoeveelheid onderdelen die we moeten hebben ter beschikking. In het jaar opgelost 2 evalueren we de effectiviteit van de lineaire transformaties om de hoeveelheid onderdelen te vinden die nodig is om aan een bepaalde bestelling te voldoen.

Opgeloste oefeningen

- Oefening 1

Controleer of de volgende transformatie t: r² → R² Het is lineair:

Oplossing

Om dit te doen, moet u ervoor zorgen dat de transformatie voldoet aan de twee voorwaarden die in het begin worden beschreven, eerst de toevoeging en vervolgens het product van een scalair voor een vector. Dus je moet twee vectoren nemen v En  of behorend tot r², ze schrijven door matrixnotatie of het opgeven van de componenten.

Deze vectoren zijn:

v = x₁, En₁

of = x₂, En₂

Eerste voorwaarde

-Herinnerend dat de componentcomponent van de vectoren worden toegevoegd, moet worden geverifieerd dat:

T (v+of) = T (v) + T (of))

T (v+of) = T (x₁+ X₂ ; En₁ + En₂))

Vanaf hier wordt verkregen dat:

T (x₁+ X₂ ; En₁ + En₂) = (x₁+ X₂; 0)

-Aan de andere kant, bij het afzonderlijk toepassen van de transformatie op elke vector:

T (x₁,En₁) + T (x₂,En₂) = (x₁,0) + (x₂,0)

Door de resulterende vectoren toe te voegen, wordt het effectief verkregen:

W = (X₁+ X₂; 0)

Aangezien beide resultaten identiek zijn, is aan de eerste voorwaarde voldaan.

Tweede voorwaarde

Nu gaan we verifiëren dat het door een scler C te vermenigvuldigen, het uit de transformatie kan gaan:

T (cv) = c⋅t (v))

Sean:

v = x₁, En₁

C.v = C⋅x₁, C⋅y₁

Dus:

T (cv) = T (C⋅x₁, C⋅y₁ ) = (C⋅x₁ , 0)

Maar we weten dat vanaf de vorige stap dat t (v) = T (x₁, En₁ ) = (X₁ , 0).

Dus omdat beide uitdrukkingen identiek zijn, wordt ook aan de tweede voorwaarde voldaan en is de transformatie lineair.

- Oefening 2

Een speelgoedwagenfabriek monteert drie voertuigmodellen: C1, C2 en C3, waarvoor u stukken A, B en C nodig hebt die respectievelijk assen, wielen en chassis zijn. De vereiste bedragen staan ​​in de volgende tabel:

De fabriek is gevraagd om 12 modellen C1, 22 C2 en 16 C3 voor te bereiden. Hoeveel stukken A, B en C zijn nodig om de bestelling te voltooien?

Oplossing

Lineaire transformatie t (x) = y wordt toegepast, waarvan het resultaat het product is tussen matrices:

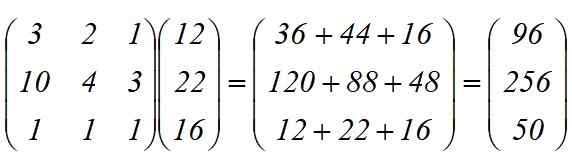
Ze zijn in totaal vereist:

-96 assen

-256 wielen

-50 chassis.

Referenties

1. Algebra en analytische geometrie. Kern en afbeelding. Classificatie van lineaire transformaties. Hersteld van: Aga.FRBA.Utn.Edu.AR.
2. Grossman, s. 2012. Lineaire algebra. 7e. Editie. McGraw Hill.
3. Gutiérrez, E. 2014. Lineaire algebra en zijn toepassingen. Patria -redactiegroep.
4. Larson, r. 2016. Fundamentals van lineaire algebra. 6e. Editie. Cengage leren.
5. Wikipedia. Lineaire toepassingen. Hersteld van: is.Wikipedia.borg.