Toroid of toro dona

We leggen uit wat een stier of stier is, zijn kenmerken, volume, oppervlakte, toepassingen en tonen verschillende voorbeelden

Wat is een toroïde?

Hij Toroïde Het is een drie -dimensionaal geometrisch lichaam in de vorm van een hoepel, ring, ring, donut of donut, vandaar de naam "Toro Dona", behorend tot de klasse van genaamd Objects Called Revolutie Solids.

Een toroid wordt gegenereerd door een gesloten platte figuur te roteren, rond een lijn die behoort tot hetzelfde vlak van de figuur, maar onderschept deze niet, zoals hieronder getoond:

Een stier, een revolutieoppervlak dat wordt verkregen door een gesloten platte figuur (als een omtrek) rond een vaste as te roteren. Bron: Wikimedia Commons

Het belangrijkste kenmerk van de toroïde is dat het, ondanks dat het een gesloten oppervlak is, een gat heeft. Dit betekent dat twee punten van het oppervlak kunnen worden verbonden door een segment dat zich buiten het object bevindt.

Een ander kenmerk van de toroïde is dat het een drie -dimensionale figuur is zonder hoekpunten. Dit kenmerk deelt het met andere volumetrische lichamen zoals de bol, maar hoewel de bol een convexe oppervlak is, is de stier tegelijkertijd concaaf en convex.

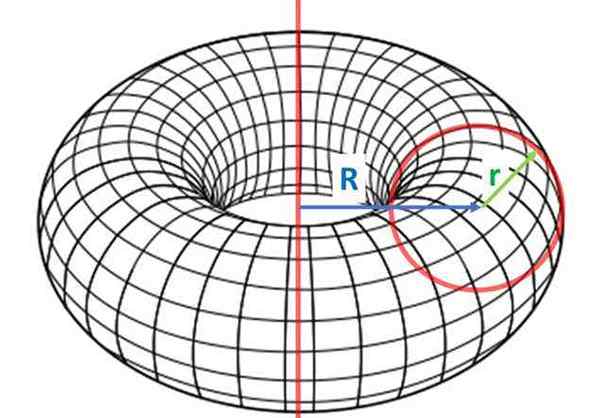
Onder de stieren, de stier Het is de meest voorkomende en wordt verkregen uit de rotatie van een radiocirkel R, Met betrekking tot een afstandsas R van de eerste. Radio R (in kleine letters) staat bekend als de kleine straal en R (kapitaal) is de grootste straal.

Volume van een toroïde

Een stier wordt gegenereerd door een gesloten vlakke oppervlakte te roteren NAAR rond een rotatieas die het niet snijdt. Duiden door R De afstand van de as tot het zwaartepunt van de vlakke figuur, het volume van de revolutiestier is:

Kan u van dienst zijn: inverse trigonometrische functies: waarde, derivaten, voorbeelden, oefeningen

V = 2πr⋅ a 

Dit resultaat wordt verkregen bij het toepassen van de Pappus stelling Voor het volume van een vaste oplossing, waarin staat dat het volume van een vaste revolutie wordt verkregen door het gebied van de figuur te vermenigvuldigen dat wordt gebroken door de omtrek van de omtrek gevormd door de rotatie van het zwaartepunt (of zwaartepunt in de zwaartekracht ) van de geroteerde figuur, rond de rotatieas.

Volume van een stier

De stier is de toroïde die wordt gegenereerd door een radiocirkel R. Als de afstand van de rotatieas tot het midden van de gedraaide cirkel R is, is het dan nodig om de stier te volumeren:

V = (2πr) ⋅ (πr²) = 2π²R³

Oppervlak van een stier

Wees een eenvoudig gerelateerde platte figuur NAAR en contour L. Als een dergelijke figuur wordt gedraaid rond een as in hetzelfde vlak van de figuur, maar dat niet kruist, dan is het gegenereerde oppervlak een gebiedsstier:

S = 2πr⋅ L

Zijnde op de afstand van de as tot het zwaartepunt of zwaartepunt, van de generatrixfiguur.

Dit resultaat is een gevolg van Pappus stelling Voor het oppervlak van een revolutie -vaste stof.

Oppervlak van een stier

De cirkelvormige kruis -sectionele stier van radio R (kleine letters) en radiom burgemeester R (hoofdletters) is een bepaalde stier genaamd Toro.

Zoals de contour l van een straalcirkel is 2πr, Dan is het gebied van het oppervlak van genoemde stier:

S = (2πr) ⋅ (2πr) = (4π²) (R⋅ r)

Toroïde toepassingen

Vanwege zijn geometrische kenmerken heeft de stier talloze praktische en culturele toepassingen. Om te beginnen zijn hoepels of ringen toroïdale onderdelen die verschillende toepassingen hebben:

Kan u van dienst zijn: minimale vierkanten

Cultureel

• Sier- of cosmetisch gebruik wanneer een ring op een vinger wordt geplaatst, of wanneer een piercing in het oor wordt geplaatst.
• In de neus van de ossen wordt een hoepel geplaatst, die dient om deze te binden en te regelen.
• Wanneer de ring of ring in de linkerhand op de ringvinger wordt geplaatst, dan heeft deze een sociale connotatie, die dateert uit de tijd van de oude Grieken, en duidt inzet, trouw en huwelijk aan het paar dat een hoepel in hetzelfde draagt manier en materiaal.

In mechanica

Buiten de sier, cosmetische en culturele context heeft de stier veel praktische toepassingen. In mechanica wordt de toroïde gebruikt als een retentiering van het lager in de voertuigaspunt. 

Ook worden de lagers van de motorvoertuigen gevormd door een of twee hoepels in een stierenvorm met verschillende vormen van dwarsdoorsnede, waarop ze cilinders of bollen rollen, met als doel wrijving in de assen te verminderen.

In elektriciteit

In elektrische toepassingen is de toroïde ook van het grootste belang, omdat de ferromagnetische kernen van inductoren, elektromagers en transformatoren vaak een stiervorm hebben en daarop een kabel in de vorm van een spoel.

De Tokamak

Er is een type gecontroleerde fusiereactor in de vorm van een toroïde of donut genoemd door zijn Russische naam: TOkamak. In dit type nucleaire fusiereactor hebben de container en de spoelen die het magnetische veld van plasma -opsluiting produceren een toroïdale vorm of dispositie.

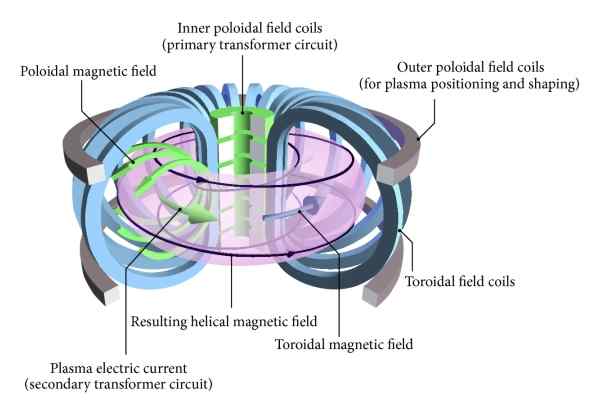De figuur toont schematisch een gecontroleerde nucleaire fusiereactor in een toroïdale vorm die bekend staat als "Tokamak". In dit type reactor hebben zowel plasma, spoelen als het magnetische veld van opsluiting een toroïdale configuratie. Bron: Wikimedia Commons

Voorbeelden

Oppervlak van een vierkante sectie stier (door formule)

In dit voorbeeld wordt een vierkante sectie -stier beschouwd zoals weergegeven in de volgende figuur:

Kan u van dienst zijn: Scaleno Triangle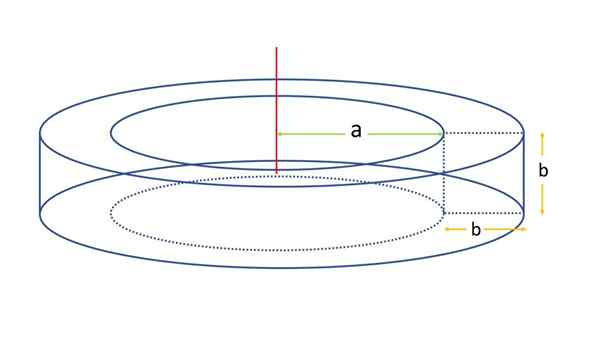 Vierkante sectie toroid. Bron: f. Zapata

Het oppervlak wordt bepaald met behulp van de oppervlakteformule voor een algemene stier. Hiertoe is het noodzakelijk om de afstand van de rotatieas tot het zwaartepunt van het vierkant te kennen, die, met behulp van de vorige nomenclatuur is R:

R = A + B/2

Het is ook nodig om de omtrek te kennen L van de generatrixfiguur, die zoals in dit geval een vierkant is aan de zijkant B, De contour zal lang zijn:

L = 4⋅B

Dan wordt de oppervlakteformule van een stier toegepast:

S = 2πr⋅l

R en L vervangen voor hun overeenkomstige uitdrukkingen, afhankelijk van de maatregelen A en B van de vierkante stier is:

S = 2π (a + b/2) ⋅4⋅B = 8π (a + b/2) ⋅B

Vierkant toroïde oppervlak (som van zijn gezichten)

De vierkante stier van de vorige figuur bestaat uit vier gezichten: de bovenste en de onderste zijn platte ringen, en het interieur en de buitenkant zijn cilindrisch.

Hiermee rekening houdend, is het mogelijk om het oppervlak te berekenen door het gebied van zijn vier gezichten toe te voegen.

De bovenste en onderste gezichten hebben een gebied gelijk aan dat van de buitenste cirkel van straal (A+B) Minder die van de binnenste cirkel van radio naar, die hierdoor hebben:

S_S= S_Je= π [(A+B)² - B²] = π⋅ [a²+ 2ab]

Het interne cilindrische gezicht heeft een gebied:

S₁= 2πab

En het externe cilindrische gezicht heeft een gebied:

S₂= 2π (a+b) b = 2πab+2πb²

Zodat de totale oppervlakte van de toroïde de som is_S+S_Je+S₁+S₂:

A = 2π⋅ [a²+ 2ab]+2πab+2πab+2πb².