Soorten hoeken, kenmerken en voorbeelden

Er zijn divers Soorten hoeken, Rekening houdend met verschillende criteria om ze te onderscheiden, kunnen ze bijvoorbeeld worden onderscheiden door hun maatregel, door de positie die ze bezetten en ook volgens de som met andere hoeken.

Meestal wordt een hoek gedefinieerd als de opening tussen twee semi -straight met een gemeenschappelijke oorsprong, de genaamd de hoekpunt van de hoek. De amplitude Opening is de maat voor de hoek, die vaak in graden of radialen komt.

Een graad is gelijk aan een van de 360 ​​delen waarin een omtrek kan worden verdeeld. Als de omtrek is verdeeld in twee gelijke delen, is elk gelijk aan 180 graden of 180º, als deze in plaats daarvan is verdeeld in vier gelijke delen, is elk 90º enzovoort. Dit systeem wordt genoemd Sexagesimal.

Radianen is een andere zeer gebruikte maatregel, die bestaat uit het nemen van een omtrek en het meten van de hoek tussen twee van zijn radio's, waarvan de lengte "R" is en met het hoekpunt in het midden van de omtrek. Op deze manier wordt de boog "s" tussen deze radio's ook beweerd "r" en de hoek wordt dan 1 radián of 1 rad en is gelijk aan 57.3e graden.

Het instrument voor het meten van hoeken is de transportband. Om een ​​maatregel te nemen, wordt het midden van de transporter samengevoegd met het hoekpunt van de hoek en een van de zijden van hetzelfde met de 0º -lijn van de transporter. De andere kant valt samen met de maat voor de hoek, die op de schaal wordt gelezen.

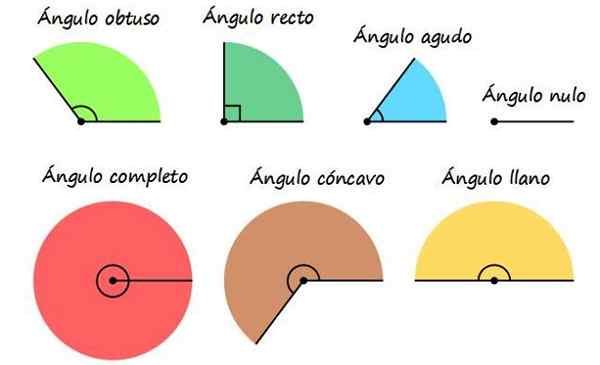
Soorten hoeken volgens uw maatregel

Classificatie van hoeken door hun maatregel. Bron: Wikimedia Commons.

Een van de meest voorkomende manieren om naar hoeken te verwijzen, is om ze te noemen volgens hun maatregel, hoewel een hoek soms tot meer dan één categorie hieronder kan behoren.

Kan u van dienst zijn: variatiecoëfficiënt: waar is het voor, berekening, voorbeelden, oefeningen

Nulhoek

Degene wiens maatregel 0º of 0 rad is, dat wil zeggen de twee semi -straight hebben een nulopening.

Scherpe hoek

De maat van een acute hoek ligt tussen 0 en 90º of tussen 0 en π/2 radialen. Bijvoorbeeld, hoeken van 30º, 45º en 60º, die deel uitmaken van de opmerkelijke hoeken, zijn allemaal acute hoeken.

Juiste hoek

Het is degene die precies 90º (π/2 radialen) meet, dit betekent dat de semi -strammen die het definiëren loodrecht op elkaar staan.  De interne hoeken van een vierkant of een rechthoek zijn rechte hoeken, en het is ook een rechte hoek die wordt gevormd tussen de kathetes van een rechthoekige driehoek.

Stompe hoek

Het is een hoek groter dan 90º of π/2 radialen.

Vlakke hoek

Het meet exact 180º, gelijkwaardig aan π radianen. Wanneer een vectoriale grootte tegengesteld is aan een andere, vormen ze een hoek van 180º, bijvoorbeeld de snelheid van een mobiel die in een rechte lijn beweegt en de vertraging ervaren wanneer deze wordt gestopt.

Convexe hoek

Wanneer een hoek minder dan 180º meet, is een convexe hoek. Een acute hoek kan convex zijn, zoals een van de 90º en die stompe hoeken waarvan de maatregel is opgenomen in 90º en 180º. Meer voorbeelden van convexe hoeken zijn:

• 45º
• 60º
• 75º
• 135º

Concave hoek

Het is degene die meer dan 180º meet, zoals 225º of 270º, de laatste is gelijk aan driekwart van de omtrek.

Volledige of perigonale hoek

De maat is 360º of 2π radianen. Het betekent dat de twee semi -strammen die het vormen opnieuw samenvallen, maar in tegenstelling tot de nulhoek, is er in dit geval een complete beurt geweest.

Kan u van dienst zijn: ovaal (geometrische figuur): kenmerken, voorbeelden, oefeningen

Soorten hoeken volgens de positie van hun zijden

In veel figuren en geometrische structuren verschijnt er meer dan één hoek en daarom is het handig om een ​​criterium te hebben om de zijkanten van de ene te vergelijken met betrekking tot de andere. Op deze manier hebben ze:

Opeenvolgende invalshoeken

De opeenvolgende hoeken staan ​​naast elkaar, daarom hebben ze een gemeenschappelijke kant en hoekpunt.

Aangrenzende hoeken

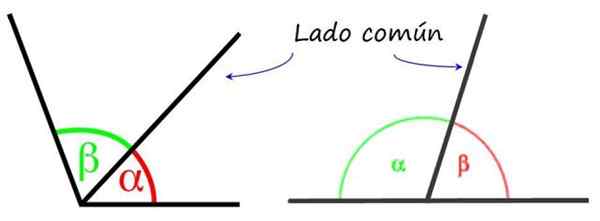Aan de linkerkant twee opeenvolgende hoeken en rechts twee aangrenzende hoeken. Bron: Wikimedia Commons/F. Zapata.

De aangrenzende hoeken hebben een gemeenschappelijke kant en hoekpunt, dat wil zeggen dat ze zich naast de andere presenteren. Maar in tegenstelling tot de opeenvolgende hoeken, zijn de resterende zijden onder de aangrenzende hoeken tegenover Semi -Straight, daarom tussen de twee hoeken in totaal 180º.

Tegenover de hoeken door het hoekpunt

De tegenovergestelde hoeken door het hoekpunt hebben het hoekpunt gemeen, en hun zijkanten strekken zich uit, van een van de hoeken naar de andere. Op deze manier hebben de tegenovergestelde hoeken door het hoekpunt dezelfde maatregel.

De volgende figuur toont 4 hoeken, aangeduid met Griekse letters. De blauwe hoeken zijn α en β, en zoals te zien, zijn ze acute en tegenovergestelde hoeken door het hoekpunt. Aan de andere kant zijn de hoeken γ en δ stompe hoeken en worden ook tegengewerkt door het hoekpunt.

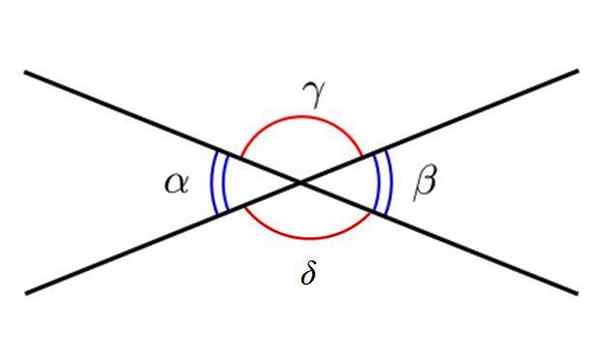Tegenover de hoeken door het hoekpunt. Bron: Wikimedia Commons.

Soorten hoeken volgens de som van hun maatregelen

Sommige berekeningen, vooral bij trigonometrie, zijn zeer vereenvoudigd door te observeren of de som van de metingen van twee hoeken die van een van de opmerkelijke hoeken is, zoals de juiste hoek (90º) of de platte hoek (180º). Volgens dit hebben ze:

Complementaire hoeken

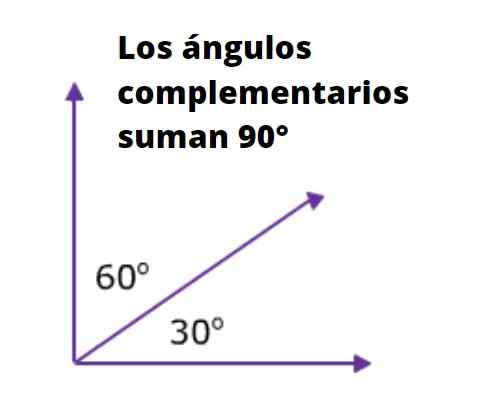
Die hoeken waarvan de som gelijk is aan 90º zijn complementair. De interne acute hoeken van een rechthoekige driehoek zijn bijvoorbeeld complementair, omdat de som van zijn drie interne hoeken gelijk is aan 180º.

Kan u van dienst zijn: 90 divisors: wat zijn en uitleg

Aangezien een van de interne hoeken van de rechthoek driehoek 90º meet, is de som van de andere twee ook gelijk aan 90º.

Aanvullende hoeken

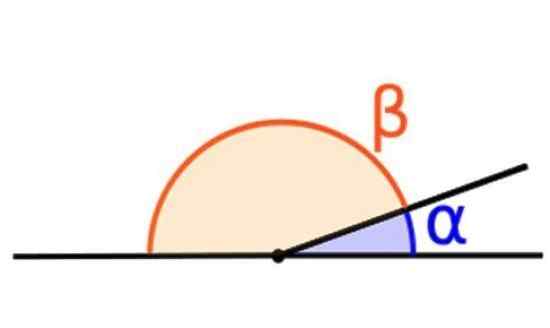De som van twee aanvullende hoeken is gelijk aan 180º. Bron: Wikimedia Commons.

Zijn die hoeken waarvan de som gelijk is aan 180º. Bijvoorbeeld de hoeken α en β getoond in de bovenste figuur.

Voorbeelden van opmerkelijke hoeken die tegelijkertijd aanvullend zijn, zijn:

• 120º en 60º
• 135º en 45º

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Baldor. 1983. Flat and Space and Trigonometry Geometry. Culturele thuislandgroep.
3. EN. NAAR. 2003. Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
4. Geometrie 1e. Hoeken in de omtrek. Hersteld van: edu.Xunta.is.
5. Rijk, B. Geometrie. 1991. Schaum -serie. 2e. Editie. McGraw Hill.