Soorten integralen
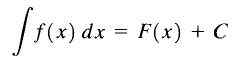
- 2405
- 666
- Alton D'Amore
De Soorten integralen dat we in de berekening zijn, zijn de onbepaalde integralen en de gedefinieerde integralen. Hoewel gedefinieerde integralen veel meer toepassingen hebben dan onbepaalde integralen, is het eerst nodig om voor onbepaalde integralen op te lossen.
Een van de meest aantrekkelijke toepassingen van de gedefinieerde integralen is de berekening van het volume van een vast van revolutie. Beide soorten integralen hebben dezelfde lineariteitseigenschappen en ook de integratietechnieken zijn niet afhankelijk van het type integraal.
Maar ondanks dat het erg op elkaar lijken, is er een belangrijk verschil; In het eerste type integraal is het resultaat een functie (die niet specifiek is), terwijl het resultaat in het tweede type een nummer is.
Basistypen van integralen
De wereld van integralen is zeer breed, maar hierin kunnen we twee basistypen integralen onderscheiden, die een grote toepasbaarheid hebben in het dagelijks leven.
1- onbepaalde integralen
Als f '(x) = f (x) voor alle x in het domein van f, zeggen we dat f (x) een antiderivatief, een primitief of een integraal van f (x) is.
Aan de andere kant, laten we opmerken dat (f (x)+c) '= f' (x) = f (x), wat impliceert dat de integraal van een functie niet uniek is, omdat het geven van verschillende waarden aan de constante C We zullen verschillende antiderivaten verkrijgen.
Om deze reden wordt f (x)+c de onbepaalde integrale van f (x) genoemd en c wordt constant van integratie genoemd en we schrijven het als volgt:
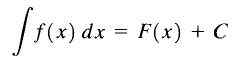 Onbepaalde integraal
Onbepaalde integraal Zoals we kunnen zien, is de onbepaalde integraal van de functie f (x) een familie van functies.
Als u bijvoorbeeld de onbepaalde integrale van de functie f (x) = 3x² wilt berekenen, moet eerst een antiderivative van f (x) worden gevonden.
Kan u van dienst zijn: TrinomialHet is gemakkelijk op te merken dat f (x) = x³ een antiderivatief is, aangezien f '(x) = 3x². Daarom kan dat worden geconcludeerd
∫f (x) dx = ∫3x²dx = x³+c.
2- Gedefinieerde integralen
Laat y = f (x) Een echte functie gaat door in een gesloten interval [a, b] en f (x) een antiderivatief van f (x). Het wordt de gedefinieerde integrale van F (x) tussen limieten A en B tot het getal f (b) -f (a) genoemd en geeft als volgt aan:
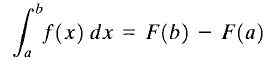 Fundamentele berekeningstelling
Fundamentele berekeningstelling De hierboven getoonde formule is beter bekend als "de fundamentele stelling van de berekening". Hier wordt "A" ondergrens genoemd en "B" wordt de bovengrens genoemd. Zoals te zien is, is de definitieve integrale van een functie een nummer.
In dit geval, als de gedefinieerde integrale van f (x) = 3x² wordt berekend in het interval [0,3], wordt een getal verkregen.
Om dit nummer te bepalen, kiezen we f (x) = x³ als antiderivatief voor f (x) = 3x². Vervolgens berekenen we f (3) -f (0) die ons als gevolg van 27-0 = 27 gooit. Concluderend is de gedefinieerde integrale van f (x) in het interval [0,3] 27.
Opgemerkt kan worden dat als g (x) = x³+3, g (x) wordt gekozen, een antiderivatief is van f (x) verschilt van f (x), maar dit heeft geen invloed op het resultaat als g (3) -g (0) = (27+3)-(3) = 27. Om deze reden verschijnt in de gedefinieerde integralen de integratieconstante niet.
Een van de meest bruikbare toepassingen die dit type integraal heeft, is dat het het gebied (volume) van een platte figuur (van een vaste revolutie) mogelijk maakt, waardoor adequate integratiefuncties en limieten (en een rotatieas) worden vastgesteld).
Onder de gedefinieerde integralen kunnen we verschillende uitbreidingen van deze vinden, zoals integrale lijnen, oppervlakte -integralen, onjuiste integralen, meerdere integralen, onder andere, allemaal met zeer nuttige toepassingen in wetenschap en engineering.
Het kan u van dienst zijn: verschil tussen cirkel en omtrek (met voorbeelden)Referenties
- Kishan, h. (2005). Integrale calculus. Atlantic Publishers & Distributors.
- Purcell, E. J., Varberg, D., & Rigdon, s. EN. (2007). Berekening (Negende ed.)). Prentice Hall.

