Steiner Verklaring Stelling, toepassingen, oefeningen

Hij Steiner's stelling, ook bekend als parallelle as stelling, Het maakt het mogelijk om het traagheidsmoment van een uitgebreid lichaam te evalueren, rond een as die parallel is aan een andere die door het massamiddelpunt van het object gaat.

Het werd ontdekt door de Zwitserse wiskundige_Cm Het traagheidsmoment van het object ten opzichte van een as die door zijn CM en ik massacentrum loopt_Z het traagheidsmoment met betrekking tot een andere parallelle as hierop.

Figuur 1. Een rechthoekige deur die zijn vreugde aanzet, heeft een traagheidsmoment dat kan worden berekend door de stelling van Steiner toe te passen. Bron: Pixabay.

Bekend de afstand D die zowel assen als de massa M van het lichaam in kwestie scheidt, is het traagheidsmoment met betrekking tot de incognito -as:

Je_Z = I_Cm + MD²

Het traagheidsmoment geeft aan hoe gemakkelijk het is om een ​​object rond een bepaalde as te roteren. Het hangt niet alleen af ​​van het lichaam van het lichaam, maar van hoe het wordt verdeeld. Om deze reden staat het ook bekend als Roterende traagheid, Uw eenheden zijn in het internationale KG -systeem . M².

De stelling laat zien dat het traagheidsmoment Je_Z Het is altijd groter dan het traagheidsmoment Je_Cm in een bedrag gegeven door M.D².

[TOC]

Toepassingen

Aangezien een object in staat is om rond talloze assen te roteren, en in de tafels meestal alleen het traagheidsmoment met betrekking tot de as die door het zwaartepunt gaat, vergemakkelijkt de stelling van Steiner de berekening wanneer het lichamen op assen op assen moet roteren die niet samenvallen met dit.

Kan u van dienst zijn: rechtlijnige beweging: kenmerken, typen en voorbeelden

Een deur draait bijvoorbeeld niet om een ​​as die door zijn massacentrum loopt, maar met betrekking tot een laterale as, waar de scharnieren zich houden.

Bij het kennen van het traagheidsmoment is het mogelijk om de kinetische energie te berekenen die is geassocieerd met de rotatie op deze as. Ja K is kinetische energie, Je het moment van traagheid rond de betreffende as en Ω Hoeksnelheid is vervuld dat:

K = ½ i.Ω²

Deze vergelijking lijkt erg op de zeer bekende formule van kinetische energie voor een massaobject M Op snelheid bewegen v:  K = ½ m.v². En is dat het moment van traagheid of roterende traagheid Je speelt in rotatie dezelfde rol als het deeg M In de vertaling.

Demonstratie van de stelling van Steiner

Het traagheidsmoment van een uitgebreid object wordt gedefinieerd als:

I = ∫R² DM

Waar DM Het is een oneindigse massa massa en R Het is de afstand tussen DM en de rotatieas Z. In figuur 2 kruist deze as het midden van de massa -cm, maar het kan iedereen zijn.

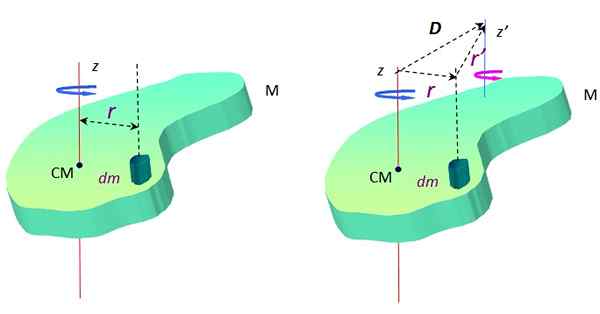Figuur 2. Een object dat wordt uitgebreid in rotatie rond twee parallelle assen. Bron: f. Zapata.

Rond een andere as  Z ', Het traagheidsmoment is:

Je_Z= ∫ (R ')² DM

Nu, volgens de driehoek gevormd door de vectoren D, R En R ' (Zie figuur 2 aan de rechterkant), er is een vectorsum:

R + R ' = D   → R ' = D - R

De drie vectoren bevinden zich in het vlak van het object dat de XY. De oorsprong van het coördinatensysteem (0,0) wordt in CM gekozen om de volgende berekeningen te vergemakkelijken.

Op deze manier de vierkante module van de vector R ' is:

Kan u dienen: Biofysica: geschiedenis, welke studies, toepassingen, concepten, methoden

(R ')² = (D_X- R_X))² +(D_En - R_En))² =

= D_X² + D_En² +R_X² + R_En2 -2D_XR_X - 2 D_EnR_En =

= D² + R²  - 2e_XR_X - 2 D_EnR_En

Nu wordt deze ontwikkeling vervangen in de integraal van het moment van traagheid i_Z en ook de definitie van dichtheid DM = ρ wordt gebruikt.DV:

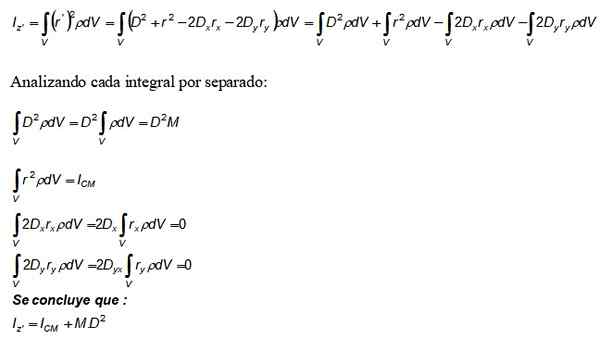
De term m. D² die in de stelling van Steiner verschijnt, komt uit de eerste integraal, de tweede is het traagheidsmoment met betrekking tot de as die door CM gaat.

Van zijn kant zijn de derde en vierde integralen 0 waard, omdat ze per definitie de positie van de CM vormen, die is gekozen als de oorsprong van het coördinatensysteem (0.0).

Opgeloste oefeningen

-Oefening opgelost 1

De rechthoekige deur van figuur 1 heeft een massa van 23 kg, 1,30 breed en 2,10 m hoog. Bepaal het traagheidsmoment van de deur met betrekking tot de as die door de vreugde gaat, ervan uitgaande dat de deur dun en uniform is.

figuur 3. Schema voor het voorbeeld opgelost 1. Bron: Modified Pixabay.

Oplossing

Van een tabel met traagheidsmomenten, voor een rechthoekige plaat van massa M en afmetingen naar En B, Het traagheidsmoment ten opzichte van de as die door het massamiddelpunt gaat, is: i_Cm = (1/12)M((naar² + B²)).

Er zal een homogene deur worden verondersteld (een aanpak, omdat de deur van de figuur waarschijnlijk niet zo veel is). In dit geval gaat het midden van de massa door zijn geometrische centrum. In figuur 3 is een as die door het massacentrum gaat getekend en die ook parallel is aan de as die door de vreugde gaat.

Je_Cm = (1/12) x 23 kg x (1.30²+2.10²) M² = 11.7 kg.M²

Kan u van dienst zijn: wat is een geoid?

Steiner's stelling aanbrengen voor de groene rotatieas:

I = i_Cm + MD² = 11.7 kg.M² + 23 kg x 0.652 m² = 21.4 kg.

-Oefening opgelost 2

Vind het traagheidsmoment van een dunne homogene staaf wanneer deze draait ten opzichte van een as die door een van de uiteinden gaat, zie figuur. Is het groter of minder dan het traagheidsmoment wanneer het draait om zijn centrum? Omdat?

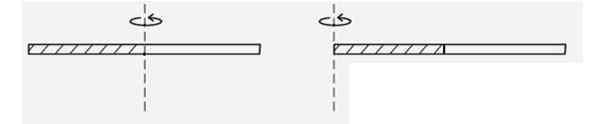Figuur 4. Schema voor het voorbeeld opgelost 2. Bron: f. Zapata.

Oplossing

Volgens de traagheidsmomenten, het moment van traagheid Je_Cm van een dunne staaf deeg M en lengte L is: Je_Cm = (1/12) ml²

En de stelling van Steiner stelt dat wanneer deze wordt gedraaid rond een as die door een uiteinde gaat D = L/2 overblijft:

I = i_Cm + MD² = (1/12) ml² + M (l/2)² = (1/3) ml²

Het is oud.

De invloed van de afstand tot de rotatieas is niet lineair, maar kwadratisch. Een massa die twee keer de afstand is die een ander een traagheidsmoment zal hebben evenredig met (2d)² = 4d².

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill. 313-340.
2. Georgia State University. Roterende beweging. Hersteld van: Phys.NTHU.Edu.Tw.
3. Parallelle as stelling. Hersteld van: hyperfysica.Phy-Astr.GSU.Edu.
4. Rex, a. 2011. Fundamentals of Physics. Pearson. 190-200.
5. Wikipedia. Parallelle as stelling. Opgehaald uit: in.Wikipedia.borg