Bernoulli stelling

We leggen uit wat de stelling van Bernoulli is, vergelijkingen, toepassingen en een oefening op te lossen

Wat is de stelling van Bernoulli?

Hij Bernoulli stelling Hij bevestigt dat, in een ideale vloeistof die in een leiding circuleert, de mechanische energie per volume -eenheid van de vloeistof constant is in alle secties van de buis, ongeacht dat ze een verschillende transversale sectie van oppervlakte en hoogte hebben.

Nu is een ideale vloeistof er een die niet kan worden gecomprimeerd, dus de dichtheid is vastgesteld, ongeacht de drukwaarde.

Bovendien heeft een ideale vloeistof geen viscositeit, dat wil zeggen dat er geen wrijving is tussen de vloeistoflagen en niet tussen de vloeistof en de wanden van het kanaal.

Voorwaarden voor niet -compresseerbaarheid en nulviscositeit zijn essentieel om de stelling van Bernoulli toe te passen. Het is ook noodzakelijk dat de stroom stationair is, dat wil zeggen dat de stroom niet in de loop van de tijd varieert.

Aan de andere kant moet de stroom laminair zijn, dus er kan geen wervelingen of turbulentie zijn tijdens de doorgang van het kanaal.

Bernoulli -vergelijking

De Bernoulli -vergelijking heeft drie termen, het werk gedaan door druk op P, kinetische energie en zwaartekrachtpotentiaal energie voor elke volumetrische dichtheidsvloeistofeenheid ρ ρ ρ ρ

Bernoulli's vergelijking is:

Aan de andere kant stelt de continuïteitsvergelijking vast dat in een ideale vloeistof de stroom constant is in alle delen van de stroombuis. Dat wil zeggen, het volume vloeistof in dezelfde tijdseenheid is hetzelfde in alle secties van de buis.

Als de stroom q is, dan:

Q = constant

Met:

Q = a · v

Waar a het dwarsdoorsnede van de buis is en V is de snelheid van de vloeistof.

Kan u van dienst zijn: kunstmatige satellieten

Opgemerkt wordt dat in de smalste delen van de buis de vloeistof sneller moet circuleren, omdat deze constant blijft, hoewel het varieert. Daarom is kinetische energie per volume -eenheid groter.

Aangezien de stelling van Bernoulli vaststelt dat mechanische energie constant is in alle secties, neemt in de smallere delen van grotere kinetische energie potentiële energie af. 

De potentiële energie bestaat uit zwaartekrachtenergie per volume -eenheid plus het werk dat wordt uitgevoerd door de druk in een eenheidsvolume, daarom vermindert het verminderen van de potentiële energie ook de druk.

Samenvattend resulteert het gecombineerde effect van het principe van continuïteit en de Bernoulli -stelling resulteert in de smalle delen van de stroombuis, waar de vloeistofsnelheid groter is, de druk daalt ten opzichte van de bredere secties.

Termen in de Bernoulli -vergelijking

1) Werk gedaan door de druk per volume -eenheid 

In een gedeelte van de dwarsdoorsnede van het gebied tot, De vloeistof beweegt een hoeveelheid S, Vanwege de druk p die een kracht f = p⋅ a produceert.

Het werk met geweld is:

F⋅ s = p⋅ a⋅ s

Aangezien het A⋅S -product het verplaatste volume vertegenwoordigt, komt het werk dat per volume wordt uitgevoerd numeriek overeen met de waarde van P in de beschouwde sectie.

2) Kinetische energie van een volume vloeistof

Omdat de vloeistof niet samendrukbaar is, heeft de dichtheid een vaste waarde genoemd ρ.

Wanneer de vloeistof circuleert door een deel van de dwarsdoorsnede A, een hoeveelheid S in een tijd t verplaatsen, is de stroomsnelheid:

Het kan u van dienst zijn: tweede wet van thermodynamica: formules, vergelijkingen, voorbeelden

v = s/t

En de kinetische energie van het genoemde vloeistofgedeelte wordt berekend door:

K = ½ ρ (a⋅s) v²

Maar als het verplaatste volume (a⋅s) eenheid is, wordt de term kinetische energie gegeven door ½ ρ V².

3) Gravitatiepotentiaal energie van een volume vloeistof van een eenheid op een hoogte h 

Voor een deegvloeistofgedeelte M en lengte H Wat een bepaald referentieniveau betreft, wordt zwaartekrachtenergie gegeven door:

U = m⋅ g⋅ h

Als het deeg M Het komt overeen met een eenheidsvloeistofgedeelte, waarna de massa van het gedeelte overeenkomt met de dichtheid ρ, Dus de potentiële energie zal zijn ρ⋅ g⋅ h.

Bernoulli Stelling Toepassingen

Aerodynamische ondersteuning

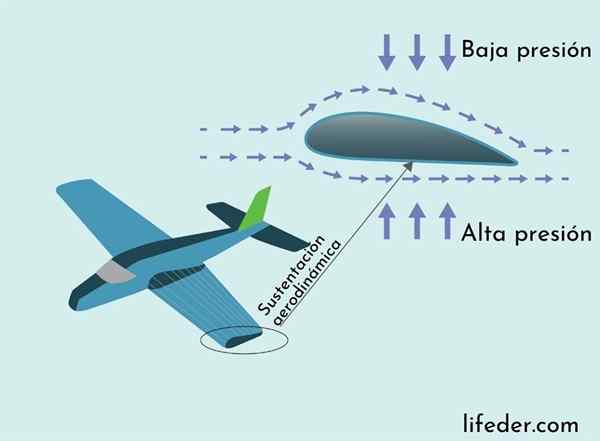Aerodynamische ondersteuning wordt verklaard door de stelling van Bernoulli

De kracht die voorkomt dat een vliegtuig van vlucht tot instorting de aerodynamische steunkracht is. De netto steunkracht is verticaal gericht en werkt langs de vlakke vleugel. De oorsprong ervan wordt verklaard door de stelling van Bernoulli.

De vleugel van een vlak heeft een dwarsdoorsnede met een langere curve aan de bovenkant en korter aan de onderkant. Dit maakt de luchtroute nabij het oppervlak van de vleugel aan de bovenkant, zodat de lucht sneller boven de vleugel stroomt dan de bodem. 

Als gevolg van de stelling van Bernoulli is de luchtdruk in het bovenste deel van de circulerende vleugel minder dan aan de onderkant, wat resulteert in de kracht die wordt uitgeoefend door het drukverschil naar boven gericht, waardoor het gewicht van het vlak wordt ondersteund, volgens het kan zijn gezien in de volgende afbeelding.

Het kan je van dienst zijn: natuurkunde tijdens de Grieken (Antige Griekenland)

Lancering van ballen en ballen met curve -effect

In sommige sporten zoals voetbal, honkbal en cricke, weten ervaren spelers hoe. Is wat wordt genoemd Effectlancering.

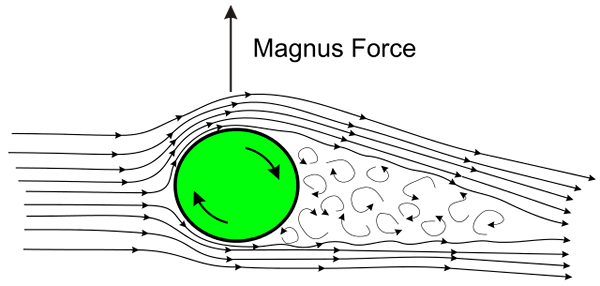Magnus effect illustratie. Bron: Wikimedia Commons

Het effect treedt op wanneer de bal of bal snel draait terwijl hij door de lucht beweegt. De rotatie veroorzaakt de lucht naar het oppervlak van de bal, wordt er door in twee tegenovergestelde richtingen gesleept, één ten gunste van de vertaalrichting en, aan de andere kant, tegen de verplaatsingsrichting.

Als gevolg van de luchtweerstand wordt een lage drukgebied geproduceerd op een gezicht van de bal en op het tegenoverliggende gezicht een hoge druk, waardoor een netto kracht wordt geproduceerd die het natuurlijke traject van de bal afleidt.

De uitleg van dit fenomeen bekend als Magnus -effect Het woont precies in de stelling van Bernoulli: waar de vloeistof snel circuleert, is de druk laag en aan de zijkant waar de druk langzaam circuleert.

Oefening opgelost

Een horizontale buis heeft een gebiedssectie a₁ = 40 vierkante centimeter en een ander deel van de gebiedssectie A₂ Vier keer lager. Als de waterstroom 6 l/s is, bepaal dan het drukverschil en het hoogteverschil in de verticale buizen.

Oplossing 

Beginnend bij de stroomvergelijking, waarvan de waarde q = 6 l/s is:

Q = a · v

Je moet dan de snelheid in het brede gedeelte 1,5 m/s en in de smalle rek 6 m/s is.

Vervolgens wordt het toepassen en matchen van de Bernoulli -vergelijking op het brede en smalle stuk, een drukverschil van 1700 PA verkregen, wat overeenkomt met een hoogteverschil in de verticale buizen van 1,72 meter.