Geschiedenis van moleculaire kinetische theorie, postulaten en voorbeelden

De Moleculaire kinetische theorie Het is er een die probeert de experimentele waarnemingen van gassen te verklaren vanuit een microscopisch perspectief. Dat wil zeggen, het probeert de aard en het gedrag van gasvormige deeltjes te associëren, met de fysieke kenmerken van gas als vloeistof; Leg het macroscopisch uit van de microscopische.

Gassen zijn altijd het object van belang geweest voor wetenschappers vanwege hun eigenschappen. Ze bezetten het hele volume van de container waarin ze zijn en kunnen volledig comprimeren zonder hun inhoud tegen de lagere weerstand; En als de temperatuur stijgt, begint de container uit te breiden en kan het zelfs barsten.

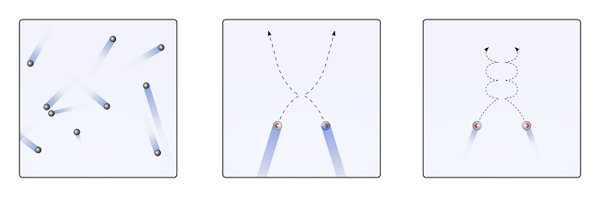Gasvormige deeltjes in verre omstandigheden of dicht bij vloeibaarheid. Bron: Olivier Cleynen en gebruiker: Sharayanan [CC BY-SA 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)]

Veel van deze eigenschappen en gedragingen zijn samengevat in de wetten van ideale gassen. Ze beschouwen echter gas als geheel en niet als een set van miljoenen verspreide deeltjes in de ruimte; Bovendien biedt het niet, van druk-, volume- en temperatuurgegevens, meer informatie over hoe deze deeltjes bewegen.

Het is dan zo dat moleculaire kinetische theorie (TCM) voorstelt ze te visualiseren als mobiele bollen (superieur beeld). Deze bollen botsen met elkaar en de wanden willekeurig en handhaven een lineair traject. Wanneer de temperatuur echter daalt en de druk toeneemt, wordt het traject van de bollen curve.

Een gas, volgens de TCM, moet zich gedragen als de bollen van de eerste beeldvak. Maar wanneer het wordt afgekoeld en de druk op hen verhoogt, gaat hun gedrag weg van het ideaal. Het zijn dan echte gassen, dicht bij vloeibaarheid en gaan naar de vloeibare fase.

Onder deze omstandigheden worden de interacties tussen de sferen belangrijker, tot het punt dat hun snelheden even langzaam zijn. Hoe dichter ze uit de vloeibaar zijn, hoe meer krommen hun trajecten (rechterbox) worden, en hun botsingen zijn minder energie.

[TOC]

Geschiedenis

Daniel Bernoulli

Het idee van deze sferen, beter genaamd Atomen, was al in aanmerking genomen door de Romeinse filosoof Lucretius; Niet voor gassen, maar voor vaste, statische objecten. Aan de andere kant paste Daniel Bernoulli in 1738 de atomaire visie toe op gassen en vloeistoffen door ze zich voor te stellen als wanordelijke bollen in alle richtingen.

Zijn werk schond destijds echter de natuurwetten; Een lichaam kon niet voor altijd bewegen, dus het was onmogelijk om te denken dat een reeks atomen en moleculen op elkaar botsten zonder verlies van hun energie; dat wil zeggen, het bestaan ​​van elastische botsingen was niet mogelijk.

Rudolf Clausius

Een eeuw later versterkten andere auteurs de TCM met een model waar gasvormige deeltjes in één richting bewogen. Rudolf Clausius stelde echter zijn resultaten op en bewapende een completer model van de TCM waarmee het de ideale gasewetten wilde verklaren die Boyle, Charles, Dalton en Avogadro hebben aangetoond.

Kan u van dienst zijn: coulombimetrie: fundamentals, typen, toepassingen

James Clerk Maxwell en Ludwig Boltzmann

In 1859 verklaarde James Clerk Maxwell dat gasvormige deeltjes een reeks snelheden vertonen bij een gegeven temperatuur, en dat een set ervan kan worden overwogen door middel van een gemiddelde moleculaire snelheid.

Vervolgens verbond Ludwig Boltzmann in 1871 bestaande ideeën met entropie, en hoe thermodynamisch altijd de neiging heeft om de maximaal mogelijke ruimte op een homogene en spontane manier in te nemen.

Postuleer de moleculaire kinetische theorie

Om gas uit zijn deeltjes te overwegen, een model waarin aan bepaalde postulaten of veronderstellingen wordt voldaan; gepostuleerd dat logisch de macroscopische en experimentele observaties moet kunnen voorspellen en uitleggen (zo trouw mogelijk). Dat gezegd hebbende, de postulaten van de TCM worden genoemd en beschreven.

Het volume gasvormige deeltjes is te verwaarlozen

In een container vol gasvormige deeltjes verspreiden ze zich en bewegen ze tussen hen door alle hoeken. Als ze zich even op een specifiek punt van de container zouden kunnen ontmoeten, zonder vloeibaarheid, zou worden opgemerkt dat ze nauwelijks een verachtelijk deel van het volume van de container bezetten.

Het betekent dat het in de container, zelfs als het miljoenen gasvormige deeltjes bevat, het echt meer leeg is dan vol (volume-vacío-verhouding veel minder dan 1); Daarom, als zijn barrières het toestaan, kunnen hij en gas binnen abrupt worden samengedrukt; Sinds gerekend zijn de deeltjes erg klein, net als hun volume.

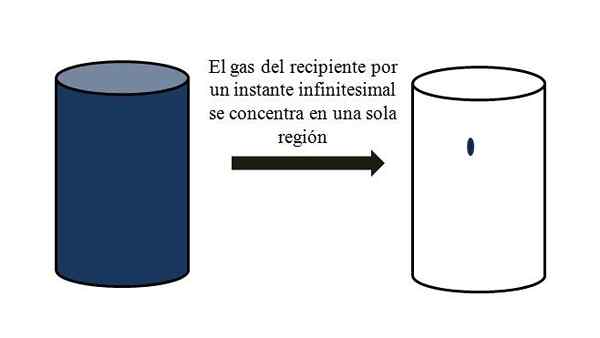Volume-vacío-relatie van een gas in een container. Bron: Gabriel Bolívar.

Het superieure beeld illustreert precies wat hierboven wordt opgemerkt, met behulp van een blauwachtig gas.

De aantrekkingskrachten tussen de deeltjes zijn nul

Gasachtige deeltjes in de container botsen met elkaar zonder voldoende tijd om hun interacties sterkte te worden; Nog minder wanneer wat hen voornamelijk omringt, is moleculair leeg. Een onmiddellijk gevolg hiervan is dat hun lineaire trajecten hen in staat stellen het volume van de container volledig te dekken.

Als het bovenstaande niet zo was, zou een "bizarre" en "labyrintische" container natte gebieden hebben als gevolg van gascondensatie; In plaats daarvan reizen de deeltjes de hele container met volledige vrijheid, zonder de sterkte van hun interacties die hen stoppen.

Kan u van dienst zijn: chloorzuur (HCLO3) Disbui van gasvormige deeltjes wanneer de interacties nietig of onbeduidend zijn (naar., lineair), en wanneer ze belangrijk zijn (B., krommen). Bron: Gabriel Bolívar.

De lineaire trajecten van het bovenste beeld (a.) demonstreer dit postulaat; Terwijl als de trajecten krommen zijn (B.), bewijs dat er interacties zijn die niet kunnen worden genegeerd tussen de deeltjes.

Gasvormige deeltjes zijn altijd in beweging

Van de eerste twee postulaten komen samen naast het feit dat gasdeeltjes nooit stoppen met bewegen. Eenmaal vervaagd in de container, botsen ze met elkaar en met de wanden van hetzelfde, met een kracht en snelheid die recht evenredig is aan de absolute temperatuur; Deze kracht is de druk.

Als de gasvormige deeltjes niet meer bewegen, zou dit worden gezien in de "rooktalen", voortkomend uit niets, met voldoende tijd om zichzelf in een vacuüm te bestellen en willekeurige manieren te geven.

De botsingen tussen de deeltjes en de wanden van de container zijn elastisch

Als de elastische botsingen tussen de gasvormige deeltjes en de wanden van de container nooit in de container zullen optreden, zal deze nooit optreden (terwijl de fysieke omstandigheden niet veranderen) de condensatie van het gas; of wat hetzelfde is als zeggen dat ze nooit rusten en ze zijn altijd botsen.

Dit komt omdat er in elastische botsingen geen nettoverlies van kinetische energie is; Een deeltje botst met de muur en stuitert op dezelfde snelheid. Als een deeltje wanneer botsing de snelheid verlaagt, versnelt de andere, zonder warmte of geluid dat de kinetische energie van een van hen afneemt.

Kinetische energie blijft niet constant

De beweging van de deeltjes is willekeurig en chaotisch, zodat niet allemaal dezelfde snelheid draagt; Zoals gebeurt bijvoorbeeld op een snelweg of in een menigte. Sommigen zijn energieker en reizen meer snelheid, terwijl anderen traag zijn, wachten op een botsing om ze te versnellen.

Om uw snelheid te beschrijven, is het dan nodig om een ​​gemiddelde te berekenen; En daarmee wordt de gemiddelde kinetische energie van de deeltjes of gasmoleculen verkregen. Aangezien de kinetische energie van alle deeltjes voortdurend verandert, maakt het gemiddelde een betere gegevensbeheersing mogelijk en kunt u met een grotere betrouwbaarheid werken.

Gemiddelde kinetische energie is gelijk aan een bepaalde temperatuur voor alle gassen

Gemiddelde moleculaire kinetische energie (EC_MP) In een container wordt het gewijzigd met de temperatuur. Bij een hogere temperatuur zal deze energie groter zijn. Omdat het een gemiddelde is, kunnen er deeltjes of frisdrank zijn die meer of minder energie hebben met betrekking tot deze waarde; sommige sneller en langzamer, respectievelijk.

Kan u van dienst zijn: zuren en basen: verschillen, kenmerken, voorbeelden

Wiskundig kan worden aangetoond dat EC_MP Het hangt uitsluitend af van de temperatuur. Dit betekent dat het niet uitmaakt wat het gas, zijn moleculaire massa of structuur, zijn EC_MP Het zal hetzelfde zijn bij een T -temperatuur en zal alleen variëren als het toeneemt of afneemt. Van alle postulaten is dit misschien het meest relevant.

En hoe zit het met de gemiddelde moleculaire snelheid? In tegenstelling tot EC_MP, Moleculaire massa beïnvloedt snelheid. Hoe zwaarder het deeltje of het gasmolecuul, het is vanzelfsprekend om te verwachten dat het langzamer gaat.

Voorbeelden

Hieronder staan ​​enkele korte voorbeelden van hoe TCM erin is geslaagd om uitleg te geven aan de wetten van ideale gassen. Hoewel ze niet worden aangepakt, kunnen andere fenomenen, zoals de verspreiding en effusie van gassen, ook worden verklaard met de TCM.

Boyle Law

Als het volume van de container wordt gecomprimeerd bij constante temperatuur, neemt de afstand die de gasvormige deeltjes moeten botsen om tegen de wanden te botsen; die gelijk is aan een toename van de frequentie van deze botsingen, wat resulteert in een grotere druk. Wanneer de temperatuur constant is, EC_MP Het is ook constant.

Charles Law

Als t, neemt EC toe_MP zal toenemen. Gasachtige deeltjes zullen sneller bewegen en een groter aantal keren botsen met de wanden van de container; verhoogt de druk.

Als de wanden flexibel zijn, in staat zijn om uit te breiden, wordt het gebied groter en zal de druk vallen totdat het constant wordt; En als gevolg hiervan zal het volume ook toenemen.

Dalton's wet

Als meerdere liters verschillende gassen in een ruime container zouden worden toegevoegd, van kleinere containers, zou hun totale interne druk gelijk zijn aan de som van de gedeeltelijke druk die elk type gas afzonderlijk uitoefent.

Omdat? Omdat alle gassen met elkaar beginnen te botsen en homogeen verspreiden; De interacties tussen hen zijn nietig en het vacuüm overheerst in de container (postulaten van de TCM), dus het is alsof elk gas alleen wordt gevonden, waardoor de druk op een individuele manier wordt uitgeoefend zonder de interferentie van de andere gassen.

Referenties

1. Whitten, Davis, Peck & Stanley. (2008). Scheikunde. (8e ed.)). Cengage Learning, p 426-431.
2. Fernández Pablo. (2019). Moleculaire kinetische theorie. Vix. Hersteld van: vix.com
3. Jones, Andrew Zimmerman. (7 februari 2019). Kinetische moleculaire gassentheorie. Hersteld van: Thoughtco.com
4. Hall Nancy. (5 mei 2015). Kinetische gassentheorie. Glenn Research Center. Opgehaald uit: grc.pot.Gov
5. Blaber M. & Lagere s. (9 oktober 2018). Basics van kinetische moleculaire theorie. Chemistry Libhethexts. Hersteld van: chem.Librhetxts.borg
6. De kinetische moleculaire theorie. Opgehaald uit: Chemed.Chem.Purdue.Edu
7. Wikipedia. (2019). Kinetische gassentheorie. Opgehaald uit: in.Wikipedia.borg
8. Toppr. (S.F.)). Kinetische moleculaire gassentheorie. Hersteld van: toppr.com