Som van vectoren grafische methode, voorbeelden, opgeloste oefeningen

De som van vectoren Het is de toevoegingsbewerking tussen vectoren die resulteert in een andere vector. Vectoren worden gekenmerkt door magnitude, en ook richting en betekenis. Daarom is het in het algemeen niet mogelijk om ze toe te voegen zoals het zou worden gedaan met scalaire hoeveelheden, dat wil zeggen het toevoegen van getallen.

De vector verkregen uit de som van verschillende vectoren wordt genoemd resulterende vector. In mechanica praten we over de resulterende kracht, dat is de vector som van alle krachten op een lichaam. Dit resultaat is gelijk aan de set of het systeem van krachten.

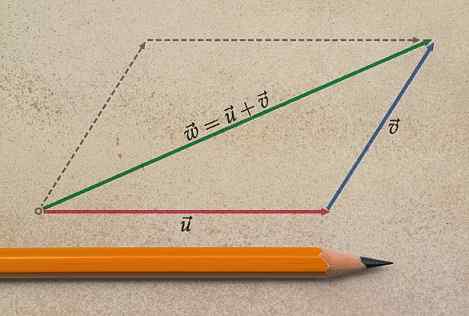
Om de somvector volledig te specificeren, is het noodzakelijk om de grootte en eenheid, richting en betekenis aan te geven.

Het is belangrijk om te benadrukken dat deze door het toevoegen van vectoren dezelfde fysieke omvang te vertegenwoordigen, daarom is de vectorsom een ​​homogene operatie. Dit betekent dat we de ene kracht met een andere kunnen toevoegen, maar geen kracht met een verplaatsing, omdat het resultaat zinloos is.

Er zijn verschillende methoden beschikbaar om de resulterende vector te vinden: afbeeldingen en analyse. Om vector -bedragen met grafische methoden te vinden, is het gebaseerd op een eenvoudige weergave voor een vector, namelijk een segment georiënteerd of pijl als deze:

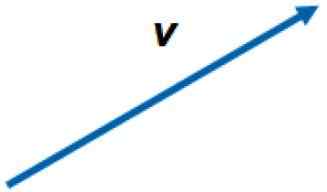Grafische weergave van een vector in het vlak. Bron: f. Zapata.

De vectoren worden aangeduid met zwarte letters in gedrukte tekst, of met een pijl over de letter, om ze te onderscheiden van hun respectieve magnitudes of van de scalaire hoeveelheden. Bijvoorbeeld de omvang van de vector v Het is gewoon v.

[TOC]

Grafische methode om vectoren toe te voegen

Om meer dan twee coupletvectoren toe te voegen, de Polygoonmethode of veelhoek, die bestaat uit het overbrengen van zichzelf naar elk van de geadresseerde vectoren. Een kenmerk van de vectoren is dat ze invariant zijn met betrekking tot de vertaling, daarom zullen we deze eigenschap gebruiken om de som te vestigen.

Kan u van dienst zijn: thermische verwijding

Het begint met een van de vectoren, omdat de vector -toevoeging commutatief is en de volgorde van de toevoegingen de som niet verandert. De tweede vector beweegt hieronder en past bij de oorsprong met het einde van de eerste.

Vervolgens wordt het naar de volgende vector gebracht en vervolgens dezelfde procedure geplaatst, die moet overeenkomen met de oorsprong met het einde van de vorige. We gaan op deze manier verder om de laatste vector te positioneren.

De resulterende vector is degene die zich bij de oorsprong van de eerste voegt met het vrije einde van de laatste. De naam van deze methode komt uit de figuur die resulteert: een polygoon.

Voorbeeld

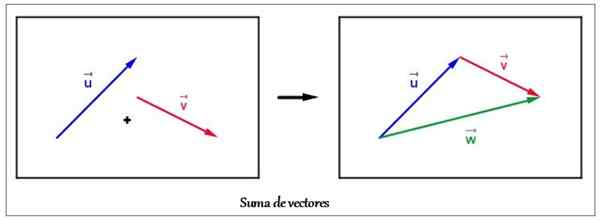
Som voorbeeld van twee vectoren in het vlak volgens de grafische methode. Bron: Wikimedia Commons

Laten we als voorbeeld de som van twee vectoren nemen of En v dat wordt getoond in de bovenste figuur.

Beginnend met de vector of, Hij verhuisde naar de vector v Om de oorsprong te matchen met het einde van de eerste. De resulterende vector W Het is afkomstig van de oorsprong van of tot het einde van v, Een driezijdige figuur vormen: een driehoek. Dat is de reden waarom in dit speciale geval de procedure wordt genoemd Driehoeksmethode.

Let op een belangrijk detail, de grootte of module van de resulterende vector is niet de som van de modules van de extra vectoren. In feite is het bijna altijd minder, tenzij de vectoren parallel zijn.

Laten we hieronder kijken wat er in dit geval gebeurt.

Speciaal geval: som van parallelle vectoren

De beschreven methode kan ook worden toegepast op het speciale geval waarin vectoren parallel zijn. Overweeg het volgende voorbeeld:

Kan u van dienst zijn: Boltzmann Constant: geschiedenis, vergelijkingen, berekening, oefeningenSom van parallelle vectoren. Bron: f. Zapata.

De vector is achtergelaten v In zijn oorspronkelijke positie, en gaat naar de vector of op zo'n manier dat zijn oorsprong overeenkomt met het einde van  v. Nu is een vector afkomstig van de oorsprong van v En het einde van of.

Dit is de resulterende vector W en de grootte is de som van de maten van de advertenties. De richting en richting van de drie vectoren is hetzelfde.

De resulterende vector heeft een maximale module als de adders een hoek van 0º vormen, zoals die van het voorbeeld. Als de vectoren een hoek van 180º met elkaar vormen, heeft de resulterende vector een minimale module.

Voorbeelden van som van vectoren

- Verplaatsingen

Een fietser reist eerst 3 km op weg naar het noorden en vervolgens 4 km west. Uw verplaatsing, die we noemen R, Het is gemakkelijk te vinden met de Triangle -methode plus een referentiesysteem, waar kardinaalpunten worden gemarkeerd:

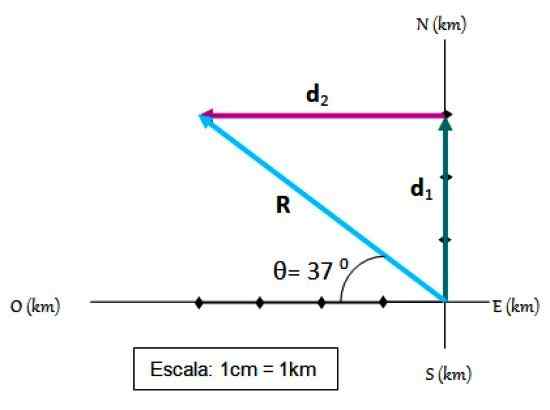Als gevolg van twee verplaatsingen. Bron: f. Zapata.

Stappen om vector toe te voegen

-Het startpunt valt samen met de oorsprong van het referentiesysteem.

-Op de coördinaatassen wordt een schaal gekozen, die in dit geval 1 cm = 1 km is

-De eerste verplaatsing is op schaal getrokken D_1.

-Dan een D₁ De tweede verplaatsing is getekend D₂, Ook op schaal.

-De resulterende verplaatsing R Het is een vector die van de oorsprong naar het einde van gaat D₂.

-De grootte van R Het wordt gemeten met een afgestudeerde regel, het is gemakkelijk te verifiëren dat r = 5.

-Eindelijk de hoek dat R Vorm met de horizontale wordt gemeten met behulp van een transporter en blijkt θ = 37 te zijn ⁰

- Resulterende snelheid

Een zwemmer wil een rivier oversteken en hiervoor niets met een snelheid van 6 km/u, loodrecht op de kust, maar een stroom die snelheid van 4 km/u draagt ​​wijkt deze af.

Het kan u van dienst zijn: OHM: weerstandsmaatregelen, voorbeelden en oefening opgelost

Om de resulterende snelheid te kennen, worden de zwemmersnelheidvectoren toegevoegd, die verticaal en stroom zijn getekend, wat horizontaal is.

Volgens de grafische methode wordt de resulterende snelheid verkregen v_R:

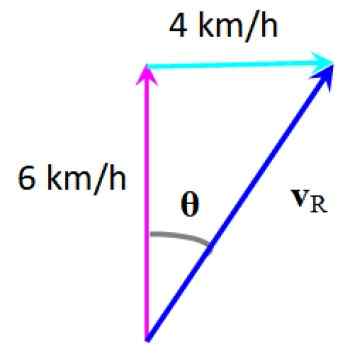Resulterende snelheid. Bron: f. Zapata.

De afwijking van de zwemmer kan worden berekend door:

θ = arctg (4/6) = 33.7e rechts van uw eerste adres

De grootte van zijn snelheid wordt verhoogd omdat de snelheid van de rivier vectorly toevoegt. U kunt zorgvuldig een schaal vinden, zoals in het vorige voorbeeld.

Of met behulp van de trigonometrische redenen van 33.7e:

Sen 33.7e = 4/v_R

v_R = 4/ sin 33.7e = 7.21 km/h

Oefening opgelost

Op een deeltje werken de volgende krachten, waarvan de grootte hieronder wordt vermeld:

F₁= 2.5 n; F₂= 3 n; F₃= 4 n; F₄= 2.5 n

Vind de resulterende kracht.

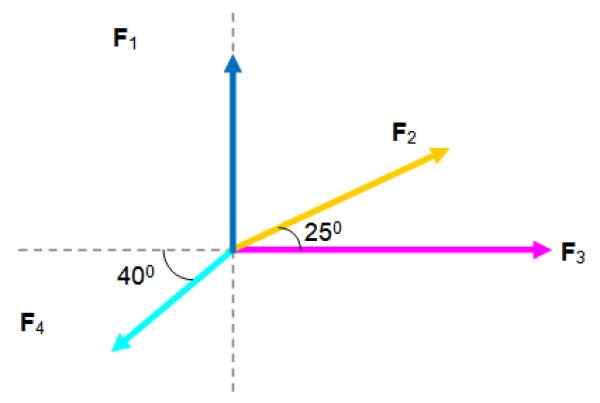Coplanar Forces -systeem. Bron: f. Zapata.

Oplossing

We kunnen grafisch toevoegen met een van de vectoren, omdat de vectorsom commutatief is.

In figuur A begon met F₁. Het opzetten van een schaal en met behulp van de regel en een ploeg worden de andere vectoren overgedragen om ze na de andere te plaatsen.

De vector F_R wordt gericht door de oorsprong van F₁ tot het einde van F₄. De omvang is 5.2 n en vormt een hoek van 26.5e ten opzichte van de horizontale.

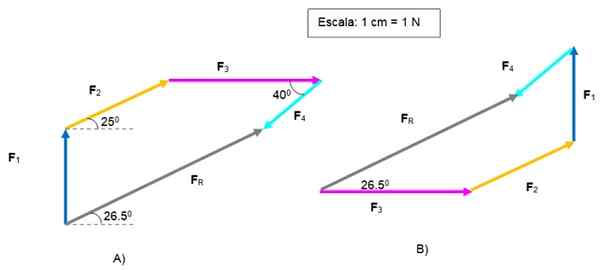Vector grafische som. Bron: f. Zapata.

In figuur B werd hetzelfde probleem opgelost, te beginnen met F₃ en eindigen met F₄, Om hetzelfde te krijgen F_R .

De polygonen zijn anders, maar het resultaat is hetzelfde. De lezer kan de volgorde van de vectoren opnieuw testen.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Bedford, 2000. NAAR. Mechanica voor engineering: statisch. Addison Wesley.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).
4. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.