Parallellogram -methode voorbeelden, opgeloste oefeningen

Hij parallellogrammethode Het is een grafische methode om twee vectoren in het vlak toe te voegen. Het wordt vaak gebruikt om het resultaat te vinden van twee krachten die op een lichaam of twee snelheden worden toegepast, zoals in het geval van een zwemmer die van plan is een rivier loodrecht te kruisen en wordt afgeleid door de stroom.

Om het parallellogram te bouwen, moeten de oorsprong van de te toegevoegd vectoren, op schaal worden getekend, samenvallen op een punt.

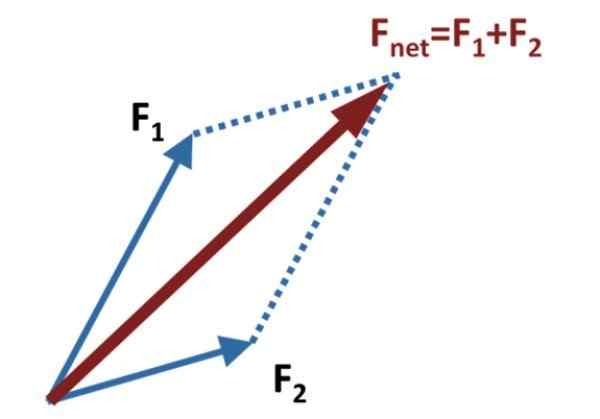
Figuur 1. De parallellogrammethode om twee vectoren toe te voegen. Bron: Wikimedia Commons.

Vervolgens worden hulplijnen parallel aan elke vector getrokken, die het uiteinde van de andere bereiken, zoals weergegeven in de bovenste figuur.

De add of resulterende vector, ook wel netto kracht genoemd, is de vector F_netto, die wordt verkregen door de vector te tekenen die gaat van de gemeenschappelijke oorsprong van F₁ En F₂, tot het punt waar de hulpparallelle lijnen kruisen. In het diagram van de figuur worden deze weergegeven door stippellijnen.

De methode ontvangt zijn naam uit de figuur die wordt gevormd met de verslaafden en de hulplijnen, die precies een parallellogram is. De belangrijkste diagonaal van parallellogram is de somvector.

Het is heel belangrijk om te benadrukken dat de volgorde waarin de extra vectoren worden geplaatst de som niet verandert, omdat deze bewerking tussen vectoren commutatief is.

[TOC]

Voorbeeld van de parallellogrammethode stap voor stap

De volgende afbeelding toont de vectoren v En of In willekeurige eenheden. De vector v Maatregelen 3.61 eenheden en vormt een hoek van 56.3e met de horizontale, terwijl of Meet 6.32 eenheden en hoek van 18.4º met betrekking tot deze referentielijn.

Kan u van dienst zijn: Willekeurige fout: formule en vergelijkingen, berekening, voorbeelden, oefeningen

Laten we vinden dat uw vector toevoegt via de parallellogrammethode.

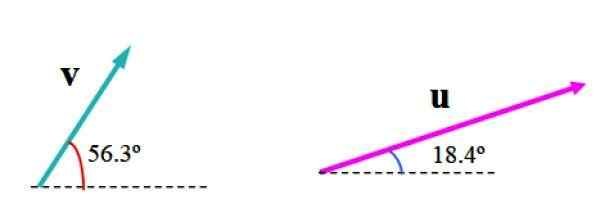Figuur 2. Alle twee vectoren in het vlak, waarvan we de resulterende vector willen vinden. Bron: f. Zapata

Het is noodzakelijk om een ​​geschikte schaal te kiezen, zoals die in de volgende figuur, waarin het vlak is gedeeld door een raster. De breedte van het vierkant vertegenwoordigt één (1) eenheid.

Aangezien de vectoren niet veranderen wanneer ze worden overgedragen, worden ze zodanig geplaatst dat hun oorsprong samenvalt met de oorsprong van het coördinatensysteem (afbeelding van links).

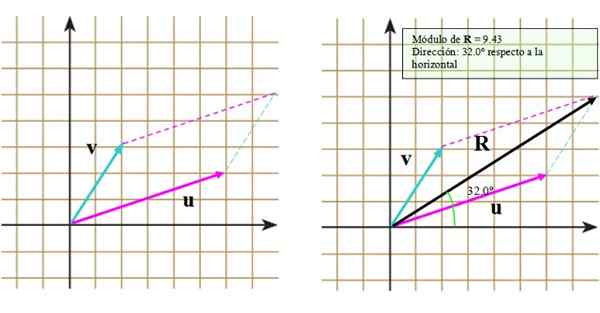figuur 3. Som van vectoren via de parallellogrammethode. Bron: f. Zapata.

Laten we nu deze stappen volgen:

1. Vector het einde van de vector v Een gesegmenteerde lijn die parallel is aan de vector of.
2. Herhaal de procedure maar deze keer met het einde van de vector of.
3. Teken de hoofddiagonaal die zich uitstrekt van de gemeenschappelijke oorsprong tot het punt van kruising van gesegmenteerde lijnen.

Het resultaat is te zien in de rechterafbeelding, waarin de resulterende vector verschijnt R.

Als we de omvang van willen weten R, We kunnen de lengte meten en vergelijken met de schaal die we hebben. En wat betreft hun richting, de horizontale as of de verticale as kan bijvoorbeeld als referenties worden gebruikt.

Door de horizontale as of x -as te gebruiken, de hoek die R vorm met deze as wordt gemeten met de transportband en op deze manier kennen we het adres van R.

Ook de omvang en richting van R Ze kunnen worden berekend door de stellingen van de cosinus en de borst, omdat het gevormde parallellogram kan worden verdeeld in twee congruente driehoeken, waarvan de zijden de modules van de vectoren zijn of, v En R. Zie het voorbeeld opgelost 1.

Kan u van dienst zijn: onmiddellijke snelheid: definitie, formule, berekening en oefeningen

Speciaal geval: som van loodrechte vectoren

Wanneer de vectoren loodrecht op elkaar staan, is de gevormde figuur een rechthoek. De resulterende vectormodule komt overeen met de lengte van de diagonaal, die gemakkelijk kan worden berekend door Pythagoras Stelling.

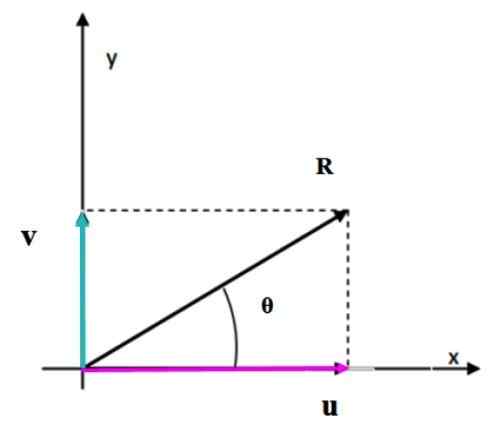Figuur 4. Som van twee loodrechte vectoren met behulp van de parallellogrammethode. Bron: f. Zapata.

Opgeloste oefeningen

- Oefening 1

Je hebt de vector v, die meet 3.61 eenheden en vormt een hoek van 56.3e met de horizontale en de vector of, wiens maatregel 6 is.32 eenheden en vormt een hoek van 18.4e (figuur 2). Bepaal de resulterende vectormodule R = of + v en de richting die genoemde vector vormt met de horizontale as.

Oplossing

De parallellogrammethode wordt toegepast volgens de hierboven beschreven stappen om de vector te verkrijgen R. Zoals eerder vermeld, als de vectoren zorgvuldig worden getrokken volgens de schaal en het gebruik van regel en transporter, grootte en richting van R Ze worden direct op de tekening gemeten.

Figuur 5.- Berekening van de grootte en richting van de resulterende vector. Bron: f. Zapata.

Ze kunnen ook direct worden berekend, met behulp van trigonometrie en de eigenschappen van de hoeken. Wanneer de gevormde driehoek niet rechthoek is, zoals in dit geval, wordt de cosinus -stelling toegepast om de ontbrekende kant te vinden.

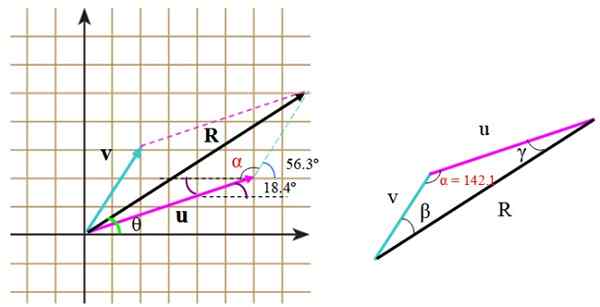
In de rechter driehoek meten de zijkanten u, v en r. Om de cosinus -stelling toe te passen, is het noodzakelijk om de hoek tussen te kennen v En of, die we met behulp van het raster kunnen vinden, waardoor de hoeken op de juiste manier worden geleverd die door de verklaring worden geleverd.

Deze hoek is α en bestaat uit:

α = (90-56.3e) + 90º +18.4e = 142.1e

Kan u van dienst zijn: rode dwerg

Volgens de stelling van Coseno:

R² = V² + of² - 2U⋅V⋅cos α = 3.61² + 6.32² - 23.61 × 6.32 × cos 142.1e = 88.98

R = 9.43 eenheden.

Eindelijk de hoek tussen R En de horizontale as is θ = 18.4 º + γ. De hoek γ kan worden gevonden door borststelling:

sin α / r = sen γ / u

Daarom:

sin γ = v (sin α / r) = 3.61 x (Sen 142.1e / 9.43)

γ = 13.6e

θ = 18.4 º + 13.6 º = 32º

- Oefening 2

Een zwemmer bereidt zich voor om een ​​rivier te oversteken die loodrecht op de stroom zwemt met een constante snelheid van 2.0 m/s. De zwemmer begint vanaf A, maar hij eindigt in B, een stroomafwaarts punt, vanwege de stroom die hem omgelezen.

Als de snelheid van de stroom 0 is.8 m/s en alle snelheden zouden de snelheid van de zwemmer moeten vinden, gezien door een waarnemer die op de kust staat.

Oplossing

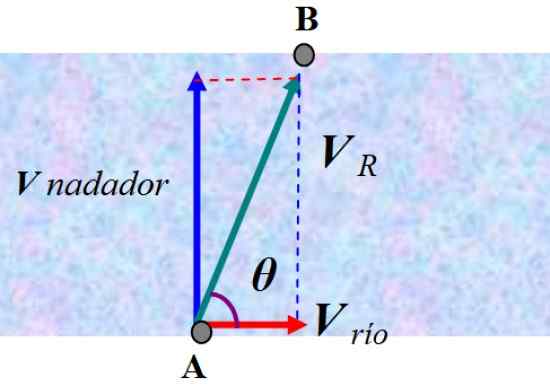Figuur 6. Som van snelheden volgens de parallellogrammethode. Bron: f. Zapata.

Een waarnemer die aan de kust staat, zou zien hoe de zwemmer wordt omgeleid volgens de resulterende snelheid V_R. Om het antwoord te vinden, moeten we de zwemmersnelheid en de snelheid van de stroming toevoegen, die we noemen V _rivier:

V _R = V _zwemmer + V _rivier

In de figuur, die niet op schaal is, zijn de vectoren toegevoegd om te verkrijgen V _R. In dit geval kan de stelling van Pythagoras worden toegepast om de omvang ervan te verkrijgen:

V_R² = 2.0² + 0.8² = 4.64

V_R = 2.15 m/s

Het adres waarin de loodrechte richtingzwemmer gemakkelijk wordt berekend, en merkt op dat:

θ = arctg (2/0.8) = 68.2e

Dan wijkt de zwemmer 90º - 68 af.2e = 27.2e van uw oorspronkelijke adres.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Bedford, 2000. NAAR. Mechanica voor engineering: statisch. Addison Wesley.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).
4. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.