Het zijn de rectilineale segmenten die mogelijk zijn in elke polygoon

De diagonaal van een vierkant

De rectilineale segmenten die mogelijk zijn in elke polygoon zijn de diagonalen. Een diagonaal is een lijnsegment dat wordt getekend door twee niet -geavanceerde hoekpunten van een polygoon samen te voegen. Met andere woorden, de diagonale lijnen beginnen bij een hoekpunt van de figuur en belanden in een andere die niet de volgende is.

In de bovenstaande afbeelding wordt de diagonaal van een vierkant getoond in een zwarte slag, die zoals te zien is, zich aansluit bij twee tegenovergestelde hoeken.

De diagonalen van de vierkant meten hetzelfde, maar in de rhombus zijn hun twee diagonalen anders, er is een grotere, langer en een kortere, kortere.

Hoe het diagonale aantal van een polygoon te berekenen?

Het bepalen van het aantal diagonalen van een polygoon kan eenvoudig zijn als het gaat om een ​​vierkant of een rhombus, maar naarmate het aantal zijden van een figuur toeneemt, wordt het ingewikkelder om te visualiseren hoeveel diagonalen het heeft.

Dit is de reden waarom een ​​eenvoudige formule die dit proces veel efficiënter zal maken, wordt gebruikt in de wiskunde:

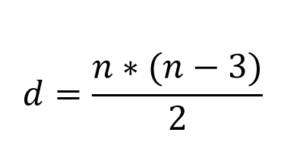
Er moet aan worden herinnerd dat N gelijk is aan het aantal zijden van de polygoon, en N moet altijd groter zijn dan 3. Omdat? (Blijf lezen, het antwoord is aan het einde).

voorbeeld 1

Bereken de hoeveelheid diagonalen van een achthoek.

De Octagon is een normale acht -zijdige polygoon, dit betekent dat alle interne zijden en hoeken hetzelfde zijn.

Met behulp van de vorige formule is het voldoende om N voor acht te vervangen:

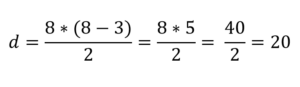
Op deze manier is het bekend dat het aantal diagonalen dat kan worden getrokken uit de hoekpunten van een achthoekige polygoon.

Het kan u van dienst zijn: gewogen media: hoe het wordt berekend, voorbeelden en oefeningen

Zonder de formule is het waarschijnlijk omslachtig om te proberen alle diagonalen te tellen, zelfs met een goede tekening. En hoe hoger de hoeveelheid zijden aan de figuur, hoe ingewikkelder het zal zijn.

Voorbeeld 2

Bereken de lengte van de diagonaal van een rechthoek met de Pythagora -stelling.

De stelling van Pythagoras bevestigt dat de som van de vierkanten van de categorieën van een rechthoekige driehoek, A en B genoemd, gelijk is aan het kwadraat van de hypotenuse (de zijde tegenover de rechte hoek), C genoemd, C wordt C genoemd).

In algebraïsche notatie zou het zijn:

naar² + B² = c²

De diagonaal van een rechthoek vormt een rechthoekige driehoek, die deze stelling kan gebruiken, waarbij B de basis is en H de hoogte is.

Als de basis 12 cm is en de hoogte 7 cm is, is deze bij het vervangen:

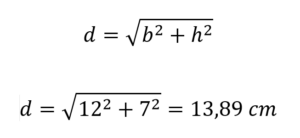
Daarom is de lengte van de diagonaal van genoemde rechthoek 13,89 centimeter.

Een polygoon zonder diagonalen

Is het mogelijk dat er een polygoon is die geen diagonale lijnen heeft? Hoe zou het zijn?

Dit raadsel kan worden gebruikt om nieuwsgierigheid bij kinderen te fotograferen en ze de diagonalen van een figuur te laten visualiseren:

De driehoek is een driezijdige polygoon en dat heeft drie interne hoeken. Maar het heeft geen diagonalen

Ja, de driehoek heeft geen diagonalen.

Uitleg

De driehoek is een driezijdige polygoon met drie interne hoeken. Maar driehoeken zijn convexe figuren die geen diagonale lijnen hebben, die de eenvoudigste en meest fascinerende polygonen van wiskunde zijn.

Ziet er goed uit in de formule waarmee u de diagonalen van een polygoon kunt berekenen:

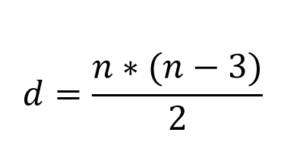
Onmiddellijk wordt opgemerkt dat het door n = 3 te vervangen, wordt verkregen als gevolg van d = 0. Dat wil zeggen, de driehoeken hebben geen diagonalen, er is geen manier om een. Maar polygonen met n = 4 hebben bijvoorbeeld alle twee diagonalen.

Kan u van dienst zijn: Decagon: regelmatig, onregelmatig, eigenschappen, voorbeelden