Revolution Solids Volume, types, opgeloste oefeningen

Hij Revolutie Solid Het is de drie -dimensionale figuur die wordt gegenereerd door rotatie van een plat oppervlak rond de axiale as of revolutieas. Figuur 1 toont een animatie van een op deze manier gegenereerde solide van revolutie.

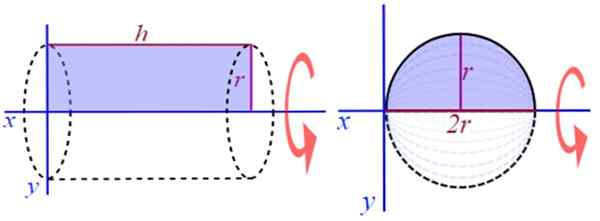
Een ander heel eenvoudig voorbeeld om te visualiseren is het genereren van een rechte cirkelvormige cilinder, het roteren van een rechthoek van hoogte of lange H en radio R, rond de positieve X -as (figuur 2). Om het volume te vinden is er een goed bekende formule:

V = basisgebied x hoogte

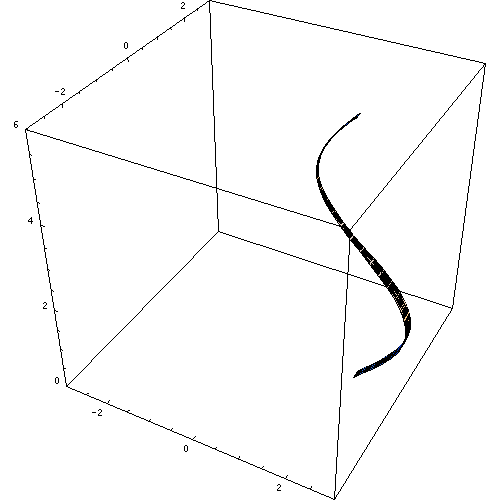Figuur 1. De figuur gegenereerd door de rotatie van een Sen X -curve. Bron: Wikimedia Commons. Macks/cc by-sa (https: // creativeCommons.Org/licenties/by-sa/2.5).

Andere revolutie -vaste stoffen zijn de bol, de rechte cirkelvormige kegel en verschillende figuren, volgens het oppervlak dat in rotatie wordt geplaatst en natuurlijk de geselecteerde as.

Figuur 2. Generatie van een rechte cirkelvormige cilinder en een bol. Bron: Wikimedia Commons.

Bijvoorbeeld, het roteren van de halve cirkel rond een lijn parallel aan de diameter wordt een vaste stof van holle revolutie verkregen.

Voor de cilinder, de kegel, de bol, zowel massief als gaten, zijn er formules om het volume te vinden, dat afhankelijk is van de straal en hoogte. Maar wanneer gegenereerd door andere oppervlakken wordt het volume berekend door gedefinieerde integralen.

[TOC]

Soorten revolutie vaste stoffen

Revolutie -vaste stoffen kunnen worden geclassificeerd volgens de curve die ze genereert:

Gebied

Het is voldoende om een ​​halve cirkel rond een as te roteren die de diameter van de Radio R -bol zal zijn. Het volume is:

V_gebied = (4/3) πr³

Kutje

Om een ​​H en Radio R -kegel te verkrijgen, het oppervlak dat moet. Het volume is:

V_Kutje = (1/3) πhr²

Cilinder

Het roteren van een rechthoek rond een axiale as die door één zijden gaat, die de korte kant of de lange zijde kan zijn, een rechte cirkelvormige cilinder van straal R en hoogte H wordt verkregen, waarvan het volume is:

Kan u dienen: touw (geometrie): lengte, stelling en oefeningen

V_cilinder = πr²H

Toroïde

De stier heeft de vorm van een donut. Het wordt verkregen door een cirkelvormig gebied rond een lijn in het vlak te roteren die de cirkel niet snijdt. Het volume wordt gegeven door:

V_Toroïde = 2πa²R

Waarbij A de straal van de dwarsdoorsnede is en R de straal van de toroïde is volgens het schema dat in de figuur wordt gepresenteerd:

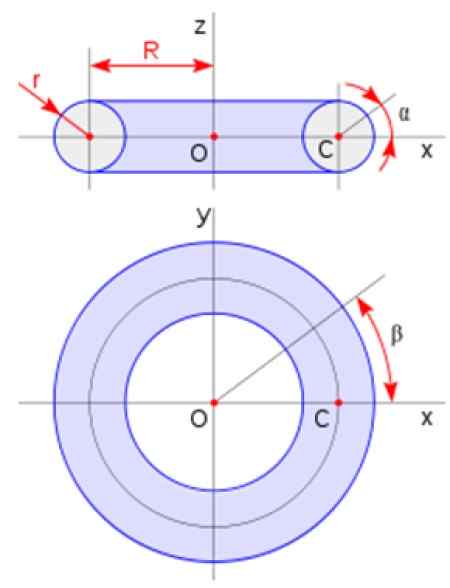figuur 3. Toroïde afmetingen. Bron: Wikimedia Commons.

Methoden voor het berekenen van het volume van een revolutie -vaste stof

Bij integrale berekening zijn deze twee methoden frequent:

-Schijven en sluitringen

-Schalen

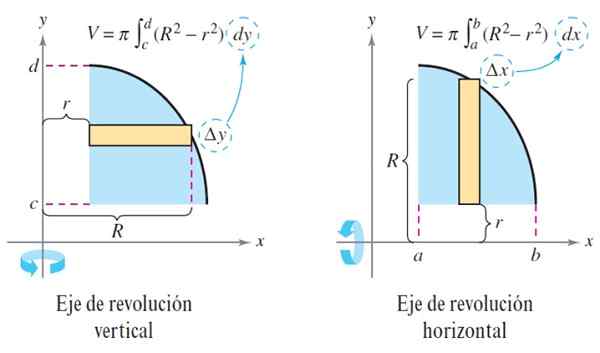
Disc -methode of sluitringen

Wanneer een vaste stof van revolutie snijdt, kan de dwarsdoorsnede een album zijn, als de vaste stof solide is of een soort wasmachine (een album met een gat in het midden), als het een solide gat is.

Stel dat een plat gebied rond de horizontale as is gedraaid. Uit dat vlakke gebied nemen we een kleine Δx breedte -rechthoek, die loodrecht rond de axiale as wordt gedraaid.

De hoogte van de rechthoek ligt tussen de buitenste curve r (x) en de meest interne r (x). Ze komen overeen met respectievelijk de externe straal en interne radio.

Bij het maken van deze rotatie wordt een AV -volume -wasmachine gegenereerd, gegeven door:

ΔV = volledig volume - gatvolume (indien aanwezig)

Onthouden dat het volume van een rechte cirkelvormige cilinder π is. radio² x Hoogte, we hebben:

ΔV = π [r²(x) - r²(x)] Δx

De vaste stof kan worden onderverdeeld in een veelheid van kleine delen van volume ΔV. Als we ze allemaal toevoegen, hebben we het volledige volume.

Om dit te doen, zullen we de neiging hebben om het volume AV te 0, dat ook erg klein wordt en een DX -differentieel wordt.

Het kan u van dienst zijn: wederzijds niet -exclusieve gebeurtenissen: eigenschappen en voorbeelden

We hebben dus een integraal:

V = ∫_naar^B π [r²(x) - r²(x)] DX

figuur 3. Wastoolmethode. Bron: Larson. R. Berekening.

In het geval dat de vaste stof vast is, dan is de functie R (x) = 0 het plakje van de gegenereerde vaste stof een schijf en blijft het volume:

V = ∫_naar^B πR²(x) DX

Wanneer de revolutieas verticaal is, nemen de vorige vergelijkingen de vorm aan:

V = ∫_naar^B π [r² (Y) - r² (y)] dy en v = ∫_naar^B πR²(Y) dy

Laag

Zoals de naam aangeeft, is deze methode om aan te nemen dat de vaste stof bestaat uit differentiële dikke lagen. De laag is een dunne buis die afkomstig is van de draai van een rechthoek parallel aan de rotatieas.

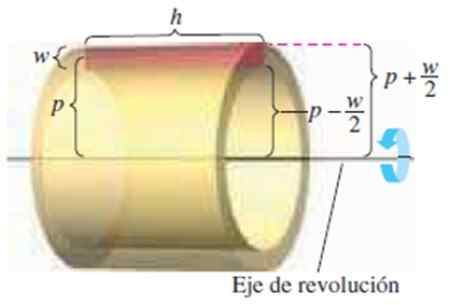Figuur 4. Een cilindrische hoogte van hoogte 2, lange h en straal P. Bron: Larson, r. Berekening.

We hebben de volgende dimensies:

-De hoogte van de rechthoek W

-Zijn lengtegraad H

-De afstand van het midden van de rechthoek tot de rotatieas P

Weten dat het volume van de laag is Buitenvolume - Binnenvolume:

π (P + W/2)²H - π (P - W/2)²H

Bij het ontwikkelen van opmerkelijke producten en vereenvoudiging wordt het verkregen:

Laag Volume = 2π⋅p⋅W⋅HHH

Laten we nu de hoogte W van de rechthoek Δy maken, zoals te zien in de volgende figuur:

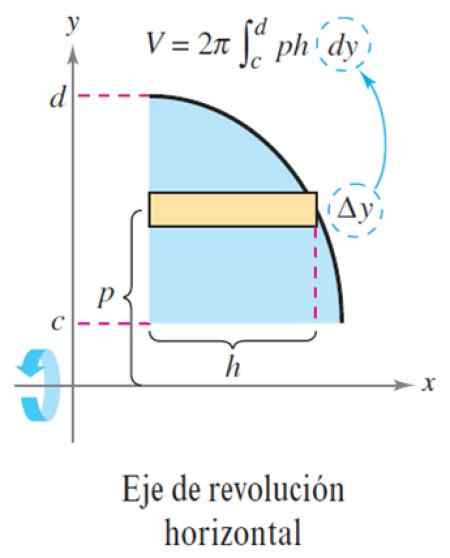Figuur 5. Horizontale revolutie -aslagenmethode. Bron: Larson, r. Berekening van een variabele.

Hiermee is het volume ΔV:

ΔV = 2π p x h x Δy

En het maken van het aantal lagen N Wees erg groot, Δy wordt een differentiële dy, zodat het totale volume de integraal is:

V = ∫_C^D 2π p (y) h (y) dy

De beschreven procedure wordt op dezelfde manier toegepast wanneer de revolutieas verticaal is:

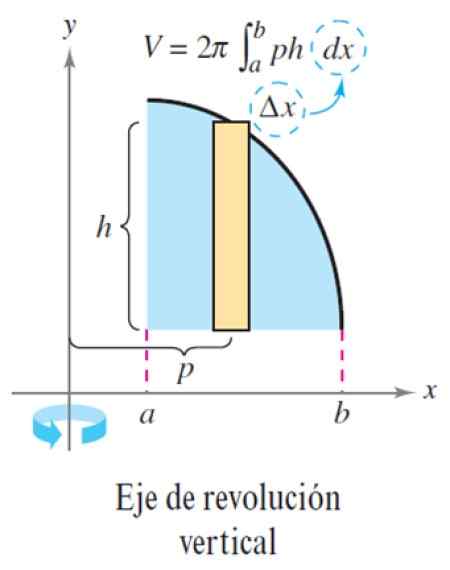Figuur 6. Laagmethode voor verticale revolutieas. Bron: Larson, r. Berekening van een variabele.

Oefening opgelost

Zoek het volume dat wordt gegenereerd door de rotatie van het platte gebied tussen de bochten:

y = x²;  y = 0; x = 2

Rond de as en.

Kan u van dienst zijn: negatieve homotecia

Oplossing

-Het eerste wat u moet doen, is de regio weergeven die de Revolution Solid zal genereren en wijst op de draaias. We hebben het in de volgende grafiek:

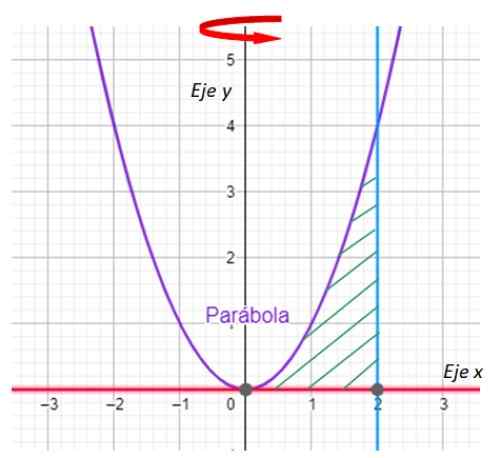Figuur 7. Grafiek van de curven voor de oefening opgelost. Bron: f. Zapata met Geogebra.

-Nu worden de kruispunten tussen de curve y = x gezocht² en de lijn x = 2. Voor zijn deel is de lijn y = 0 niemand minder dan de x -as.

Het is gemakkelijk te waarschuwen dat de gelijkenis en lijn elkaar kruisen op het punt (2,4), dat wordt bevestigd door x = 2 te vervangen op y = x².

-Vervolgens wordt een van de methoden om het volume te berekenen gekozen, bijvoorbeeld de laagmethode met verticale revolutieas:

V = ∫_naar^B 2π p (x) h (x) dx

Stap 1: Teken de rechthoek

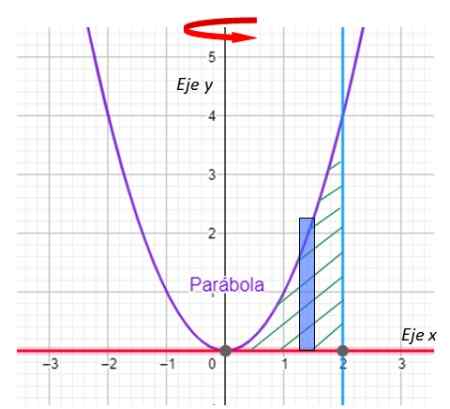Figuur 8. Rechthoek voor het opgeloste voorbeeld. Bron: f. Zapata met Geogebra.

Belangrijk: In de laagmethode is de lange zijde van de rechthoek parallel aan de rotatieas.

Stap 2: Bepaal P (x)

De laag van de laag is X

Stap 3: Bepaal h (x)

De hoogte van de rechthoek wordt bepaald door gelijkenis x².

Stap 4: Stel en lost het volume -integraal op

De integratievariabele is X, die varieert tussen 0 en 2, hiermee hebben we de integratielimieten. Expressies vervangen voor P (x) en H (x)

 Sommige oefeningen kunnen volgens beide methoden worden opgelost. Kan de lezer dit oplossen met de wasmetingsmethode?

Referenties

1. Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
2. Purcell, E. 2007. Berekening met analytische geometrie. 9NA. Editie. Pearson Education.
3. Wikipedia. Revolutie. Opgehaald uit: in.Wikipedia.borg.
4. Wikipedia. Toroïde. Hersteld van: is.Wikipedia.borg.
5. Wolfram Mathworld. Revolutie. Hersteld van: Mathworld.Wolfraam.com.