Axiale symmetrie -eigenschappen, voorbeelden en oefeningen

De Axiale symmetrie Het treedt op wanneer de punten van een figuur samenvallen met de punten van een andere figuur door middel van een rechte mediatrix genaamd Symmetry Axis. Het wordt ook radiale, rotatie- of cilindrische symmetrie genoemd.

Het wordt meestal toegepast in geometrische figuren, maar het is gemakkelijk van aard waarneembaar, omdat er dieren zoals vlinders, schorpioenen, planken of goed mensen zijn die axiale symmetrie presenteren.

Op deze foto van de horizon van de stad Toronto wordt en de weerspiegeling ervan in de water -axiale symmetrie tentoongesteld. (Bron: Pixabay)

[TOC]

Hoe de symmetrische axiale te vinden

Om de symmetrische axiale p 'van een P -punt te vinden ten opzichte van een lijn (l) worden de volgende geometrische bewerkingen uitgevoerd:

1.- De loodrecht op de lijn (L) wordt getraceerd die door punt P passeert.

2.- De onderschepping van de twee lijnen bepaalt een punt of.

3.- De lengte van het PO -segment wordt gemeten, vervolgens wordt deze lengte gekopieerd op de lijn (PO) beginnend bij of in de richting van P A of het bepalen van het punt P '.

4.- Punt P.

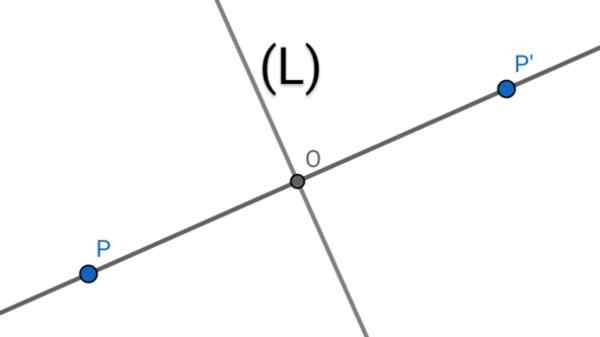Figuur 1. Twee punten p en p 'zijn axiaal symmetrisch voor een as (l) als de genoemde as mediaTrix van het PP -segment is'

Eigenschappen van axiale symmetrie

- Axiale symmetrie is isometrisch, dat wil zeggen de afstanden van een geometrische figuur en de overeenkomstige symmetrische.

- De maat van een hoek en die van zijn symmetrische zijn hetzelfde.

- De symmetrische axiale van een punt op de symmetrieas is het punt zelf.

Het kan u van dienst zijn: Gauss-Seidel-methode: uitleg, toepassingen, voorbeelden

- De symmetrische lijn van een lijn parallel aan de symmetrieas is ook een kraam evenwijdig aan de genoemde as.

- Een secant lijn naar de symmetrieas is symmetrisch.

- Het symmetrische beeld van een lijn is een andere lijn die een hoek vormt met de symmetrieas van dezelfde maat als die van de oorspronkelijke lijn.

- Het symmetrische beeld van een lijn loodrecht op de symmetrieas is een andere lijn die de eerste overlapt.

- Een lijn en zijn axiale symmetrische lijn vormen een hoek waarvan de bissector de symmetrieas is.

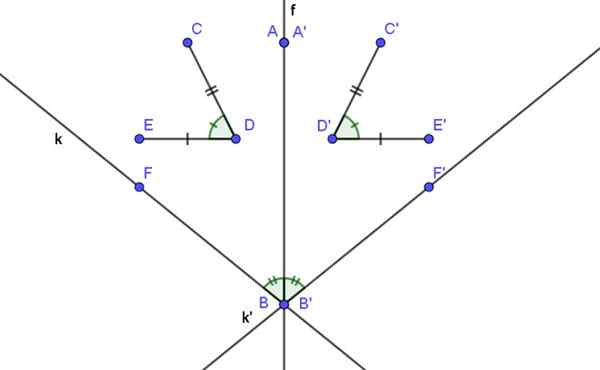Figuur 2. Axiale symmetrie behoudt afstanden en hoeken.

Voorbeelden van axiale symmetrie

De natuur vertoont overvloedige voorbeelden van axiale symmetrie. U kunt bijvoorbeeld de symmetrie van de gezichten zien, van insecten zoals vlinders, de reflectie op oppervlakken van rustig water en spiegels of de bladeren van de planten, onder vele anderen.

figuur 3. Deze vlinder vertoont bijna perfecte axiale symmetrie. (Bron: Pixabay) Figuur 4. Het gezicht van dit meisje heeft axiale symmetrie. (Bron: Pixabay)

Axiale symmetrieoefeningen

Oefening 1

U hebt de driehoek van hoekpunten A, B en C waarvan de Cartesiaanse coördinaten respectievelijk A = (2, 5), B = (1, 1) en C = (3.3) zijn. Vind de Cartesiaanse coördinaten van de symmetrische driehoek ten opzichte van de y -as (as van de ordinaten).

Oplossing: Als een punt P coördinaten (x, y) heeft, is het symmetrisch ten opzichte van de as van de ordinaten (y-as) p '= (-x, y). Met andere woorden.

Kan u van dienst zijn: oneindige set: eigenschappen, voorbeelden

In dit geval zal de symmetrische driehoek van hoekpunten A ', B' en C 'coördinaten hebben:

A '= (-2, 5); B '= (-1, 1) en c' = (-3, 3) zoals kan worden gecontroleerd in figuur 6.

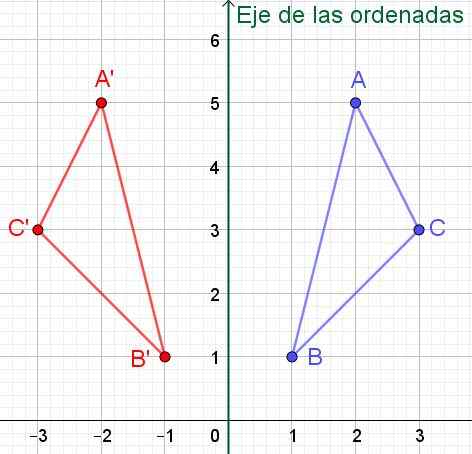Figuur 6. Als een punt coördinaten (x, y) heeft, heeft het symmetrisch ten opzichte van de y-as (as van de ordinaten) coördinaten (-x, y).

Oefening 2

In verwijzing naar de ABC -driehoek en zijn symmetrische a'b'c 'van oefening 1, controleer of de overeenkomstige zijden van de oorspronkelijke driehoek en zijn symmetrische dezelfde lengte hebben.

Oplossing: Om de afstand of lengte van de zijkanten te vinden, gebruiken we de Euclidische afstandsformule:

d (a, b) = √ ((bx-ax)^2 + (by-ay)^2) = √ ((1-2)^2 + (1-5)^2) = √ ((-1 )^2 + (-4)^2) = √ (17) = 4.123

Vervolgens wordt de lengte van de symmetrische zijde die overeenkomt met 'B' berekend:

D (a ', b') = √ ((bx'-ax ')^2 +(by'-y^2) = √ ((-1 +2)^2 +(1-5)^2) = √ ((1)^2 + (-4)^2) = √ (17) = 4.123

Op deze manier wordt bewezen dat axiale symmetrie de afstand tussen twee punten behoudt. De procedure kan worden herhaald voor de andere twee zijden van de driehoek en zijn symmetrisch om de invariantie in de lengte te controleren. Bijvoorbeeld | AC | = | A'c '| = √5 = 2,236.

Oefening 3

In verband met de ABC -driehoek en zijn symmetrische a'b'c 'van oefening 1, controleer je dat de overeenkomstige hoeken van de oorspronkelijke driehoek en hun symmetrische dezelfde hoekige maatregelen hebben.

Oplossing: Om de metingen van de hoeken te bepalen BAC en B'A'C 'Het scalaire product van de vectoren zal eerst worden berekend Aab met AC en dan het scalaire product van A'b ' met A'c '.

Onthouden dat:

A = (2, 5), B = (1, 1) en C = (3.3)

A '= (-2, 5); B '= (-1, 1) en C' = (-3, 3).

Je hebt:

Aab = Y AC =

op dezelfde manier

A'b ' = Y AC =

Kan u van dienst zijn: Lamy Stelling

Vervolgens worden de volgende scalaire producten gevonden:

Abs = ⋅ = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7

Op dezelfde manier

A'b'⋅a'c ' = ⋅ = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7

De maat van de BAC -hoek is:

∡bac = arccos ( Abs / (|AB |⋅ |AC |)) = 

Arccos (7 / (4.123⋅2,236)) = 40,6º

Evenzo is de maat voor de hoek B'a'c ':

∡b'a'c '= arccos ( A'b'⋅a'c ' / (|A'b '|⋅ |A'c '|)) = 

Arccos (7 / (4.123⋅2,236)) = 40,6º

Concluderend dat axiale symmetrie de maat van hoeken behoudt.

Oefening 4

Wees een punt P van coördinaat (a, b). Zoek de coördinaten van zijn symmetrische axiale p 'ten opzichte van de lijn y = x.

Oplossing: We zullen (a ', b') bellen naar de coördinaten van het symmetrische punt p 'met betrekking tot de lijn y = x. Het middelpunt m van het segment pp 'heeft coördinaten ((a+a')/2, (b+b ')/2) en is ook op de lijn y = x, dus aan de volgende gelijkheid wordt voldaan:

A + A '= B + B'

Aan de andere kant heeft het segment PP 'in afwachting van -1 omdat hij loodrecht is op de lijn y = x van helling 1, dus aan de volgende gelijkheid wordt voldaan:

B - b '= a' -a

Het opruimen van de twee gelijkheden voorafgaand aan 'en B' wordt geconcludeerd dat:

a '= b en wat b' = a.

Dat wil zeggen, gegeven een punt P (a, b), zijn symmetrische axiale ten opzichte van de lijn y = x is p '(b, a).

Referenties

1. Arce m., Blázquez S en anderen. Vliegtuigtransformaties. Hersteld van: educutmxli.Bestanden.WordPress.com
2. CC -berekening. Axiale symmetrie. Teruggewonnen uit: berekening.DC
3. Superprof. Axiale symmetrie. Hersteld van: superprof.is
4. Wikipedia. Axiale symmetrie. Hersteld van: is.Wikipedia.com
5. Wikipedia. Symmetrie cirkelvormig. Opgehaald uit: in.Wikipedia.com