Symmetrie

Wat is symmetrie?

De symmetrie Het is wanneer de delen van een figuur exact overeenkomen, in grootte, vorm en positie. Als je een afbeelding, object, object of leef met een denkbeeldige lijn en beide kanten hetzelfde bent, kun je zeggen dat het symmetrisch is. 

Deze denkbeeldige lijn wordt de symmetrieas genoemd en in dezelfde figuur kunnen er verschillende symmetrische assen zijn die het verdelen, gelijke delen genereren die precies samenvallen als de superpones.

Symmetrisch hart, met symmetrieas

Een heel eenvoudige manier om te bevestigen als een figuur dat we op een vel papier hebben symmetrisch is, is het tekenen van een rechte lijn in de helft van de tekening en vervolgens de figuur te buigen. Als beide partijen het ermee eens zijn, is deze figuur symmetrisch met betrekking tot de lijn die u volgt, en als ze niet samenvallen, heeft het mogelijk geen symmetrie of dat u de rechte lijn op een andere manier moet trekken.

Asymmetrie en symmetrie

Als we zeggen dat een figuur asymmetrisch is, bedoelen we dat het niet door de helft kan worden gedeeld door een lijn, om twee gelijke delen te verkrijgen. De volgende boom is bijvoorbeeld asymmetrisch:

Asymmetrische boom

Als u uw eigen lichaam onderzoekt, kunt u ook voorbeelden van symmetrie vinden. Observeer je handen zorgvuldig, beide hebben een gedeeltelijke symmetrie, omdat ze er veel uitzien, ze hebben een vergelijkbare maat, ze hebben vijf vingers en één nagel op elke vinger. 

De symmetrie is in dit geval niet compleet omdat de vingerafdrukken verschillen tussen de ene hand en een andere, en omdat elke hand kan rekenen op kleine kenmerken die het onderscheiden van de andere, zoals wonden, littekens of geboortemarkeringen, zoals maan. 

Symmetrie in de oudheid

In de oudheid waren de Grieken van mening dat de mooiste mensen degenen waren die een symmetrisch gezicht hadden, en men geloofde dat symmetrie een kenmerk was dat perfectie demonstreerde. 

Kan u van dienst zijn: lineaire programmering: waar is het voor, modellen, beperkingen, toepassingen

Dit idee van symmetrie als iets perfect is aanwezig geweest op verschillende tijdstippen van de mensheid. In feite is een van de beroemdste werken in de geschiedenis De Vitruviaanse man, Opgesteld door de Italiaanse kunstenaar van de Renaissance Leonardo da Vinci.

De Vitruviaanse man

Deze tekening wordt juist gebruikt om aan te tonen welke symmetrie in dit geval wordt toegepast op het menselijk lichaam. 

Waar kunnen we symmetrie meer vinden?

We kunnen symmetrie vinden in tekeningen, in de biologie, waar zowel planten- als dierorganismen symmetrische eigenschappen kunnen presenteren.

Ook in geometrie, in alledaagse objecten, en kan ook aanwezig zijn in muziek en literatuur, omdat er muzikale composities zijn die symmetrisch zijn, evenals teksten en gedichten die deze eigenschap hebben. 

Een gemeenschappelijke procedure bij het maken van muziekstukken is om sequenties te plaatsen met herhaling van geluiden steeds opnieuw. Het gebeurt ook dat een muzikale zin redenen heeft die identiek worden herhaald of die meer acuut of serieuzer worden herhaald. 

In het geval van literatuur is het mogelijk om zinnen te bouwen zodat ze gelijk lezen van links naar rechts, zoals: 

Ik zeg rozen, ik geef het niet, Dat, als u het investeert, zegt precies hetzelfde. 

In poëzie wordt symmetrie ook veel gebruikt in relatie tot de verzen die een gedicht vormen. 

Voorbeelden van symmetrie

Symmetrische figuren kunnen heel eenvoudig of zeer complex zijn. En je kunt beelden vinden met symmetrie zowel in geometrie als in kunst, evenals in het echte leven. 

- De onderste vlinder heeft een symmetrieas en is symmetrisch. Maar er zijn andere gevallen waarin afbeeldingen twee of meer symmetrische assen hebben.

Kan u van dienst zijn: cilindrische coördinaten: systeem, verandering en oefeningen

- Als je dit figuur observeert, zul je merken dat het twee assen van symmetrie heeft, één verticaal en één horizontaal: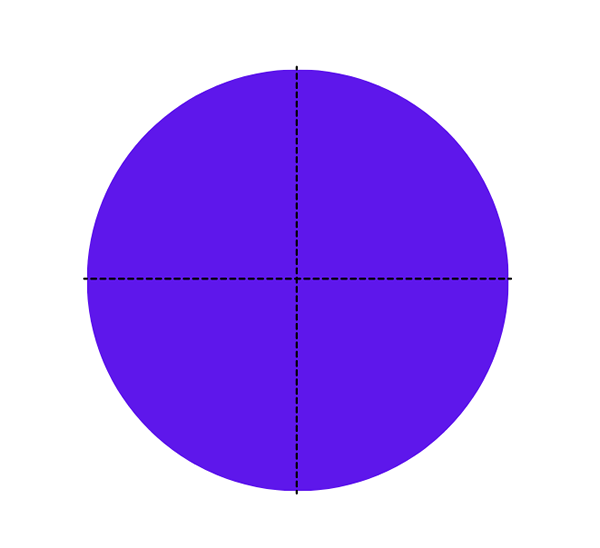

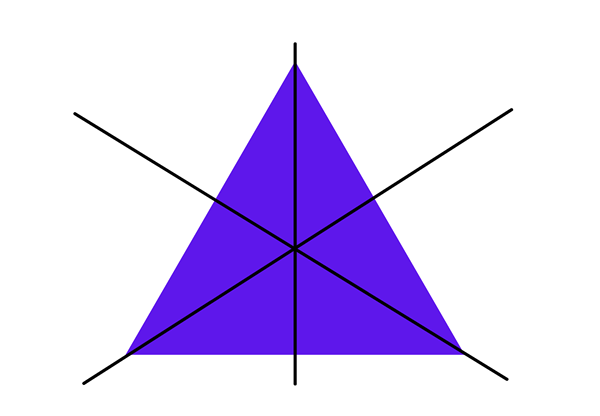
- Deze driehoek is een geometrische figuur met drie assen van symmetrie. Bij het trekken van een van deze drie lijnen zal het resultaat zijn dat de figuur wordt verdeeld in twee identieke delen.

- In deze ster kunt u vier assen van symmetrie vinden:

- Bilaterale symmetrie bij dieren. Het is een soort symmetrie dat de verdeling van een organisme in de rechter en linkerhelft impliceert, gescheiden door een as.

- Er zijn ook andere voorbeelden in de natuur die een ander type symmetrie presenteren dat bekend staat als radiale symmetrie, en dat wordt gekenmerkt omdat je het organisme kunt draaien en het beeld ervan blijft hetzelfde. De zeester zijn organismen die radiale symmetrie hebben. 

- Wanneer we het hebben over expansiesymmetrie, verwijzen we naar dat waarin de partijen dezelfde vorm hebben, maar ze groeien in grootte, zoals met de reeks Russische poppen die bekend staan ​​als Matrioskas.

- Andere soorten symmetrie zijn de symmetrie van neerslachtigheid, die wordt bereikt in twee gelijke delen van een object wanneer een beurt van 180 graden wordt gemaakt.

- De symmetrie van vertaling verwijst naar een reeks herhalingen die een object uitvoeren op een altijd identieke afstand van de as, wat genereert dat de vorm wordt herhaald langs een constante lijn, zoals bij de kolommen van een Griekse tempel. 

Symmetrieoefeningen: tekeningen

U kunt ook uw eigen symmetrische tekeningen thuis maken, met behulp van tekeningen zoals deze. Je moet de zon en de paraplu tekenen zodat het deel dat rechts van de symmetrieas is, gelijk is aan de linkerkant.

Kan u van dienst zijn: graad van een polynoom: hoe deze is bepaald, voorbeelden en oefeningen

Zon

Paraplu

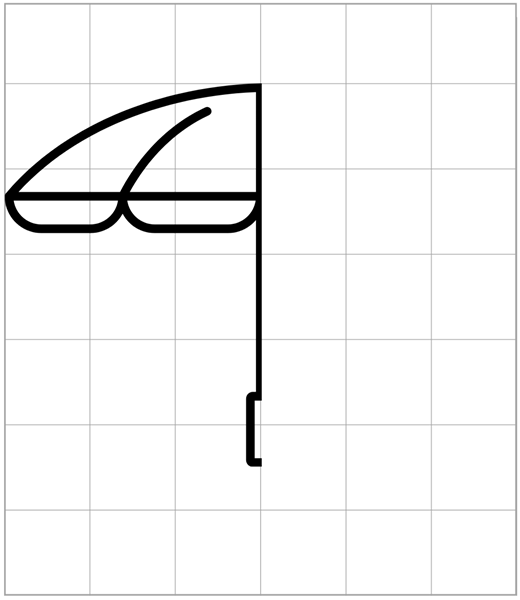
Een andere manier om een ​​symmetrisch figuur op papier te maken, is door een blad met rooster in tweeën te vouwen en met een dikke down trekking op half gevouwen half. Het idee is dat de marker het papier doorbrengt, en dus, wanneer u het ontvouwt, hebt u een symmetrische figuur gemaakt met betrekking tot de lijn die de vouw in het blad vormt.