Hefboomregel

Wat is de hendelregel?

De hefboomregel Het is een wiskundige procedure waarmee de breuken, percentages of hoeveelheden van de fasen in balans kunnen worden berekend binnen een binair systeem. Het is niet alleen wiskundig, maar ook vrij grafisch en assertief, die erg nuttig is in fysicochemische en technische berekeningen.

Deze regel is van toepassing op fasediagrammen voor binaire systemen, ongeacht het type systeem zelf. Dat wil zeggen, de fasen kunnen solide zijn, zoals bij de legeringen; of vloeistof en gasvormig, zoals we zien in systemen in vloeistofvapor-evenwicht.

Het fysieke en wiskundige principe van de hendel wordt ook gebruikt voor chemische doeleinden en in de fysica van de materialen. Bron: Jimbowley, CC BY-SA 3.0, via Wikimedia Commons

De hendelregel kan direct worden toegepast, rekening houdend met de grafische waarden in de as van de abscis, waarbij de globale breuken of percentages van de meest vluchtige component meestal gaan, in het geval van vloeistoffen; of vuurvast, in het geval van metalen in hun legeringen.

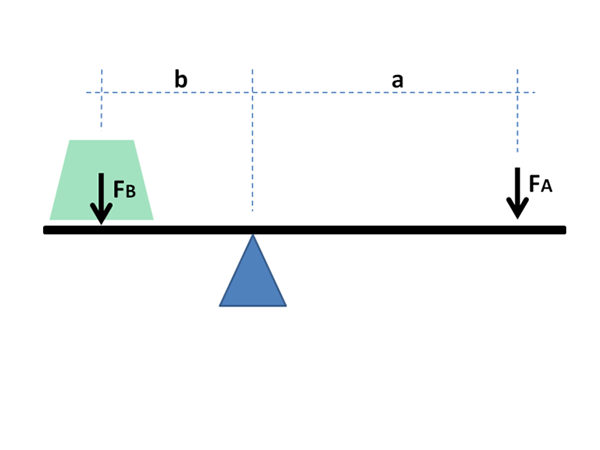
Zoals hieronder zal worden gezien, is de naam te wijten aan de enorme gelijkenis die het heeft met de wiskundige uitdrukkingen die de balans aantonen tussen twee massa's aan de uiteinden van een rocker met Fulcro.

De hendelarmen moeten in evenwicht zijn om de massa van de belastingen in evenwicht te brengen; In het geval van fasediagrammen, breuken en mol van de fasen in materiaalevenwicht.

Uitleg

Grafische aspecten

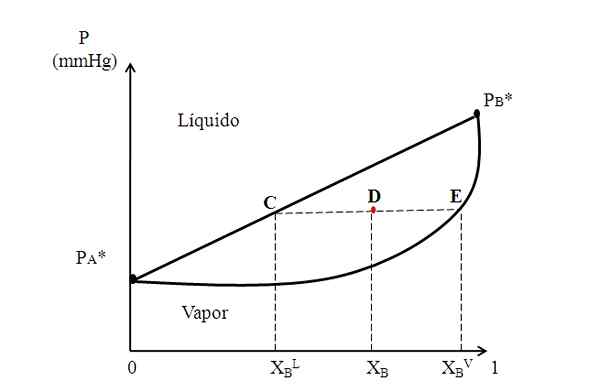Hypothetisch binair diagram waarbij een bindlijn de samenstellingen van de vloeistof- en stoomfasen toont. Bron: Gabriel Bolívar.

In het midden van het diagram hierboven hebben we een gebied waar vloeistof en stoom naast elkaar bestaan; dat wil zeggen, het evenwichtsgebied vloeistof-damp. Boven dit gebied zal het mengsel van A en B vloeibaar zijn, en eronder zullen frisdrank zijn vanwege de lagere drukken.

Overweeg nu een mengsel met een X -compositie_B en wiens druk het op punt D positioneert. We putten uit de punt D een horizontale lijn die de lijn en de curve aan de zijkanten raakt, respectievelijk afkomstpunten C en E. Deze lijn, die punten C, D en E, C-D-E, communiceert, is degene die bekend staat als de lijn van Union, en door deze naar de as te projecteren en moet ons de druk van het systeem geven.

Het kan u van dienst zijn: ALKALINITEIT VAN WATER: wat is, vastberadenheid en belang

Vervolgens trekken we uit deze punten andere lijnen loodrecht op de bindlijn, die de X -as speelt. Omdat punt E op de stoomcurve ligt, hebben we de molaire fractie van B in de stoomfase (x_B^V)). Evenzo geeft punt C op de rechte lijn van vloeistof ons de molaire fractie van B in de vloeibare fase (x_B^L)).

De hendelregel is precies gebaseerd op de bindlijn en de afstanden tussen x_B^L, X_B en x_B^V.

Wiskundige aftrek

De globale molaire fractie van B is gelijk aan:

X_B = N_B / ((N^L + N^V))

Waar N_B Ze zijn het totale mol B zowel in de vloeistof- als stoomfase, als N^L En N^V zijn de respectieve moedervlekken voor deze fasen. Opruiming N_B we zullen hebben:

N_B = X_BN^L + X_BN^V (1)

Aan de andere kant, N_B Het is ook gelijk aan:

N_B = N_B^L + N_B^V

= X_B^LN^L + X_B^VN^V  (2)

Equalations (1) en (2) zullen ons nu egaliseren:

X_BN^L + X_BN^V = X_B^LN^L + X_B^VN^V

En herschikken:

N^L(X_B - X_B^L) = N^V(X_B^V - X_B) (3)

N^L(C-d) = N^V(VAN)

Deze laatste twee wiskundige uitdrukkingen zijn de hendelregel. Merk op dat x_B - X_B^L Het is de afstand tussen punten C en D; en x_B^V - X_B, Het is de afstand tussen punten D-E: de twee helften van de bindlijn (hefboomarmen).

Deze vergelijking lijkt erg op die van het beschrijven van de balans van de massa op een rocker met Fulcro:

M₁l₁ = m₂l₂

De hendelregel stelt ons dus in staat om het totale mol te berekenen N^L En N^V op voorwaarde dat het totale mol van het mengsel bekend is, N_T ((N_T = N^L + N^V)).

Tweede vorm

De vorige uitdrukking voor de hendelregel dient om de hoeveelheden te berekenen (massa's, mol, enz.) van de fasen in evenwicht. De bekendste versie van de hendelregel stelt ons echter in staat om de breuken of percentages van elke fase te berekenen, waarbij we alleen de afstanden tussen x nemen_B, X_B^L en x_B^V.

Overweeg hetzelfde systeem hierboven, met een andere vorm van de hendelregel:

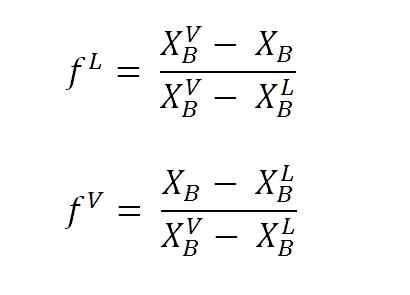Vergelijkingen om vloeistof- en stoomfracties te berekenen met behulp van de hendelarmen. Bron: Gabriel Bolívar.

Waar F ^L En F ^VHet zijn molaire fracties (of percentage, afhankelijk van de grafiek) van respectievelijk de vloeistof- en dampfasen. Merk op dat, uiteraard, F ^L En F ^V Ze hebben geen eenheden; terwijl N^L En N^V Ja ze hebben eenheden (mollen, gram, enz.)).

Kan u van dienst zijn: reactiewarmte

Voorbeelden

Methode 1

In een container zijn 28 mol B en 12 mol van A gemengd. Bepaal de hoeveelheden en molaire fracties voor de gevormde fasen.

We berekenen x_B:

X_B = (28 mol B)/ (28 mol B + 12 mol A)

= 0.7

Deze waarde komt overeen met x_B van het bovenste diagram. De onderscheppingen geven ons ongeveer de volgende waarden voor x_B^L en x_B^V:

X_B^L = 0.41

X_B^V = 0.94

Met de hendelregel:

N^L(X_B - X_B^L) = N^V(X_B^V - X_B))

En weten dat N_T = N^L + N^V, En? N_T = 40 mol, dan wissen we N^L of N^V afhankelijk van de andere:

N^L(X_B - X_B^L) = (40 mol - N^L) (X_B^V - X_B))

Herschikken en opruimen N^L we zullen hebben:

N^L = (40 mol) (x_B^V - X_B) / (X_B^V - X_B^L))

Onthoudt deze uitdrukking niet dat van F ^L? Nu vervangen we:

N^L = (40 mol) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 mol in vloeibare fase

We kunnen berekenen N^V Op twee manieren:

N^V = N^L(X_B - X_B^L) / (X_B^V - X_B))

of

N^V = 40 mol - 18.11 mol

= 21.89 mol in dampfase

Methode 2

Wat als we eerst berekenen F ^L En F ^V?

F ^L = (X_B^V - X_B) / (X_B^V - X_B^L))

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 of 45.28%

Dat wil zeggen 45.2% van de mol bevindt zich in een vloeibare fase, die die hoeveelheid gelijk is aan:

N^L = F ^LN_T

= (0.4528) (40 mol)

= 18.11 mol

EN F ^V We kunnen het even op twee manieren berekenen:

F ^V = 1 - F ^L

of

F ^V = (X_B - X_B^L) / (X_B^V - X_B^L))

Zijn waarde zijn:

F ^V = 0.5472 of 54.72%

En daarom, N^V Het zal gelijk zijn aan:

N^V = F ^VN_T

= (0.5472) (40 mol)

= 21.89 mol

Merk op dat het toepassen van de twee vormen van de hendelregel als alternatieve berekeningsmethoden, dezelfde resultaten kunnen worden bereikt. Methode 2 lijkt directer en eenvoudiger; Maar als het zorgvuldig wordt waargenomen, zodra de clearing is opgelost N^L of N^V, Het zal zien dat beide methoden eigenlijk even eenvoudig zijn.

Opgeloste oefeningen

Vervolgens zullen twee andere oefeningen worden opgelost, waarbij nu de beschouwde systemen een vloeistof-vaste en niet-vloeistof-damp omvatten. Ook zijn de diagrammen grafisch met betrekking tot de systeemtemperatuur en niet op hun druk.

Oefening 1

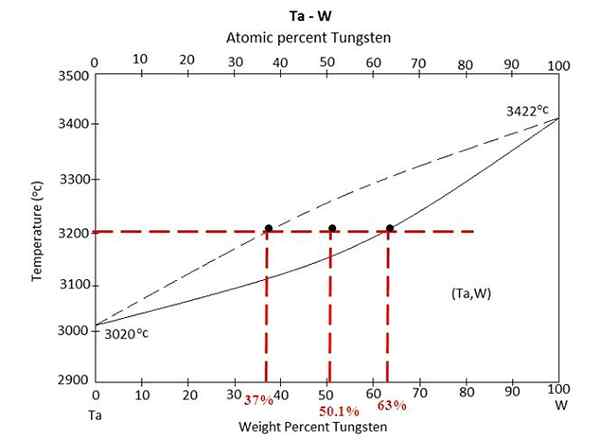Fasediagram voor een legering tussen tantalo en wolfraam. Bron: MaterialsPedia, CC BY-SA 4.0, via Wikimedia Commons

We hebben het fasediagram boven een legering tussen Tantalo en Tungsten, TA-W. Op de X -as zijn de globale massapercentages van wolfraam, w% (m/m) vertegenwoordigd.

Binnen het vloeistofevenwichtsgebied (Ta+W) en vaste stof (legering) is er een mengsel bij 3200 ºC. Bepaal de massa's van elke fase, ervan uitgaande dat 100 gram van de legering is verwarmd.

Het kan u van dienst zijn: metalen, niet -metalen en metalloïden

Procedure

Deze keer wordt de oefening opgelost met behulp van de tweede vorm van de hendelregel. De Union Line vertelt ons dat: in de vaste fase hebben we 63% van wolfraam, terwijl we in de vloeibare fase 37% Tungsten hebben. Dit komt omdat de wolfraam smelt tot een hogere temperatuur (3422 ºC) dan de tantale (3020 ºC).

Dus we hebben:

W%^S of w_S= 63%

W%^L of w_L= 37%

En ook:

W₀ = 50.1%

We passen de hendelregel toe op F ^L:

F ^L = (63% - 50.1%) / (63% - 37%)

= 0.4961 of 49.61%

Merk op dat de afstand die overeenkomt met de vloeibare fase de hendelarm in de buurt van de vaste fase, de andere kant van het middelgrote punt.

De massa van de vloeibare fase is daarom:

(0.4961) (100 gram) = 49.61 gesmolten gram

En de vaste fase zal gelijk zijn aan:

100 gram - 49.61 gram = 50.39 gram legering rijk aan wolfraam

Oefening 2

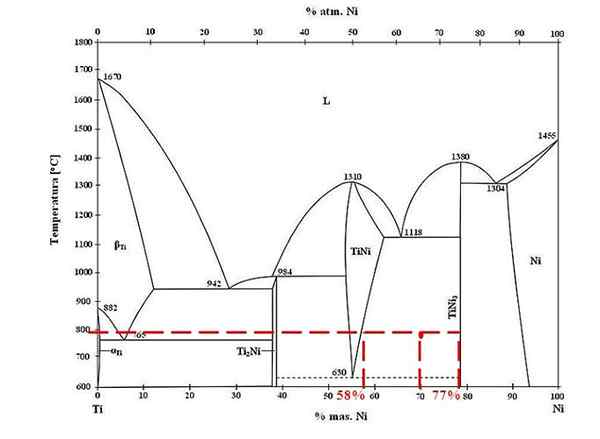Fasediagram voor titanium-nickel legeringen. Bron: Doomgiver, CC BY-SA 3.0, via Wikimedia Commons

Voor de titanium en nikkellegering bij 800 ºC, en met 70% nikkel, bepaal dan hoeveel van Tini en Tini₃ Ze zijn aanwezig.

Procedure

Deze keer vragen ze alleen om de massafracties van elke fase. Het rode punt bevindt zich in het evenwichtsgebied tussen de Tini- en Tini -fasen₃, wiens curven is waar het de lijn van de unie speelt die stroomt naar de waarden van 58% of voor de Tini -fase, en 77% of voor de Tini -fase₃.

Merk op dat het rode punt dichter bij de Tini -fase ligt₃ die van de Tini -fase. Dit betekent dat er meer tini moet zijn₃ die tini; En daarom de afstand of de hendelarm die overeenkomt met Tini₃ Het moet de langste zijn, het tegenovergestelde (70%-58%).

Dit wetende, gaan we verder met berekenen F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 of 63.16%

Inderdaad, 63.16% van de legering komt overeen met de Tini -fase₃. Ondertussen komt de tini -fase overeen met:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 of 36.84%

Concluderend tot de verhoogde oefeningen kunnen we zeggen dat de hendelregel zeer nuttig is om de breuken van elke fase in evenwicht te bepalen voor een systeem met twee componenten.

Referenties

1. Walter J. Moore. (1963). Fysische chemie. In chemische kinetiek. Vierde editie, Longmans.
2. Iran. Levine. (2009). Principes van fysicochemie. Zesde editie. MC Graw Hill.
3. Wikipedia. (2020). Hefboomregel. Opgehaald uit: in.Wikipedia.borg
4. Michael Adewumi. (18 mei 2020). De hendelregel. Hersteld van: Eng.Librhetxts.borg
5. Adam Warren. (1997). Fasediagrammen: stropdaslijnen en de hendelregel. Hersteld van: Southampton.AC.Uk
6. Universiteit van Cambridge. (2020). De hendelregel. Opgehaald uit: DOITPOMS.AC.Uk