Rechterhandregel

Figuur 1. Rechterhandregel. Bron: Wikimedia Commons. Acdx [cc by-s (http: // creativeCommons.Org/licenties/by-sa/3.0/]].

Wat is de rechterhandregel?

De rechterhandregel Het is een mnemonische bron om de richting en richting van de vector als gevolg van een vectorproduct of kruisproduct vast te stellen. Het wordt veel gebruikt in de natuurkunde, omdat er belangrijke vectorgroottes zijn die het resultaat zijn van een vectorproduct. Dat is bijvoorbeeld het geval van koppel, magnetische kracht, hoekmomentum en magnetisch moment, bijvoorbeeld.

Wees twee generieke vectoren naar En B wiens kruisproduct is naar X B. De module van een dergelijke vector is:

naar X B = naar.B.sin α

Waarbij α de minimale hoek is tussen naar En B, Terwijl A en B hun modules vertegenwoordigen. Om vectoren van hun modules te onderscheiden, worden gewaagde letters gebruikt.

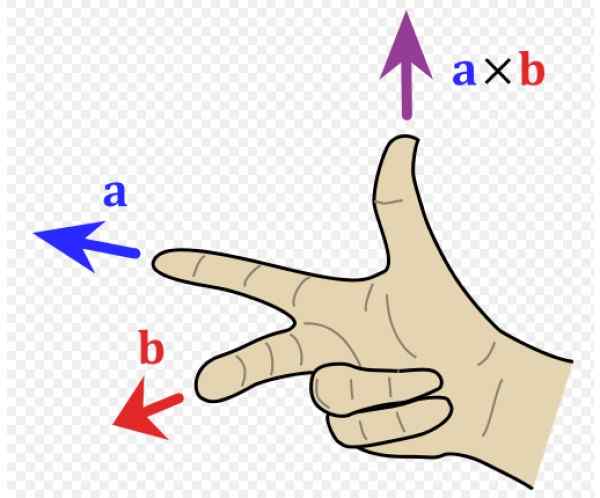
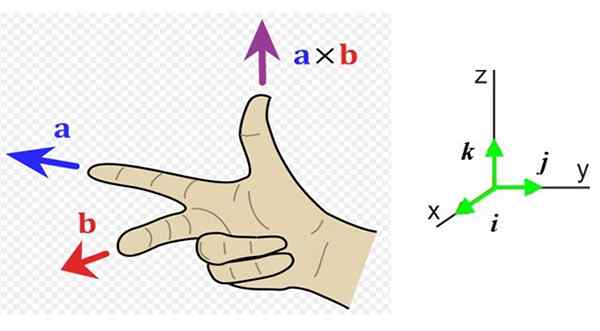
Nu moeten we de richting en betekenis van deze vector kennen, dus het is handig om een ​​referentiesysteem te hebben met de drie richtingen van de ruimte (figuur 1 rechts). De eenheidsvectoren Je, J En k Ze wijzen respectievelijk naar de lezer (uit de pagina), naar rechts en naar boven.

In het voorbeeld van figuur 1 links, de vector naar gaat naar links (adres En negatieve en wijsvinger van de rechterhand) en de vector B gaat naar de lezer (adres X positief, middelvinger van de rechterhand).

De resulterende vector naar X B heeft de duimrichting, in de richting Z positief.

Tweede regel van de rechterhand

Deze regel wordt veel gebruikt als er magnitudes zijn waarvan de richting en de betekenis roteren, zoals het magnetische veld B geproduceerd door een dunne en rechtlijnige draad die een stroom transporteert.

In dit geval zijn de magnetische veldlijnen concentrische omtrek met de draad en wordt de richting van de bocht als volgt verkregen met deze regel: de rechterduim geeft de richting van de stroom aan en de resterende vier vingers zijn gebogen in de richting van de richting van het veld. We illustreren het concept in figuur 2.

Kan u van dienst zijn: Elastische schokken: in een dimensie, speciale gevallen, oefeningen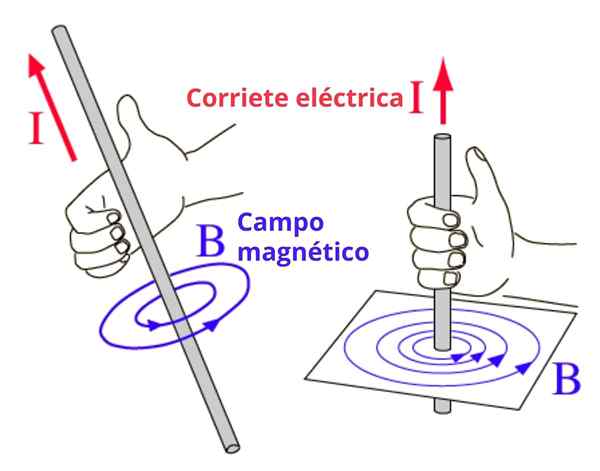Figuur 2. Rechterhandregel om de betekenis van de magnetische veldcirculatie te bepalen

Alternatieve regel van de rechterhand

De volgende figuur toont een alternatieve vorm van de rechterhandregel. De vectoren die in de verlichting verschijnen, zijn:

• Snelheid v van een punctuele belasting die.
• Het magnetische veld B waarbinnen de belasting beweegt.
• F_B De kracht die het magnetische veld uitoefent op de belasting.

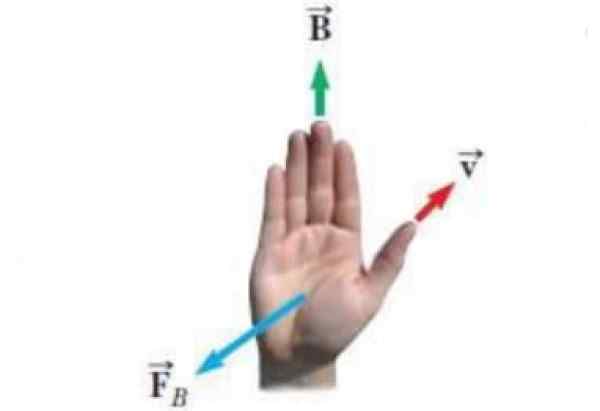figuur 3. Alternatieve regel van de rechterhand. Bron: Wikimedia Commons. Experticuis [cc by-sa (https: // creativeCommons.Org/licenties/by-sa/4.0)]

De vergelijking voor magnetische kracht is F_B = qv X B en de regel van de rechterhand om de richting en het gevoel van te kennen F_B Het is zo van toepassing: de duimpunten volgens V, de resterende vier vingers worden geplaatst volgens veld B. Dus F_B Het is een vector die uit de handpalm van de hand komt, loodrecht erop, alsof het de belasting duwt.

Let daar op F_B zou in de tegenovergestelde richting wijzen als de lading die negatief was, omdat het vectorproduct niet commutatief is. In werkelijkheid:

naar X B = - B X naar

Toepassingen

De rechterregel kan worden toegepast op verschillende fysieke magnitudes, laten we er enkele weten:

Hoeksnelheid en versnelling

Beide hoeksnelheid Ω Zoals hoekversnelling α Het zijn vectoren. Als een object rond een vaste as draait, is dit mogelijke hoeksnelheid Ω.

Van zijn kant de hoekversnelling α zal hetzelfde adres hebben als Ω, Maar de betekenis ervan hangt af van als Ω verhoogt of vermindert de omvang ervan in de loop van de tijd. In het eerste geval hebben beide dezelfde richting en betekenis, maar in de tweede hebben ze tegengestelde zintuigen.

Kan u van dienst zijn: Watt Law: wat is voorbeelden, aanvragen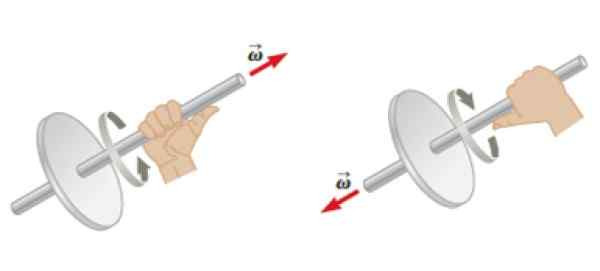Figuur 4. De rechterhandregel toegepast op een object in rotatie om de richting en richting van hoeksnelheid te bepalen. Bron: Serway, r. Fysiek.

Het hoekmomentum

De hoekige vector L_OF van een deeltje dat rond een bepaalde as roteert of wordt gedefinieerd als het vectorproduct van zijn onmiddellijke positievector R  en de hoeveelheid lineaire beweging P:

L = R X P

De rechter -handregel wordt op deze manier toegepast: de wijsvinger wordt in dezelfde richting en richting geplaatst R, De middelvinger in de P, beide op een horizontaal vlak, zoals in de figuur. Automatisch strekt de duim zich verticaal omhoog uit en wijst op de richting en richting van hoekmomentum L_OF.

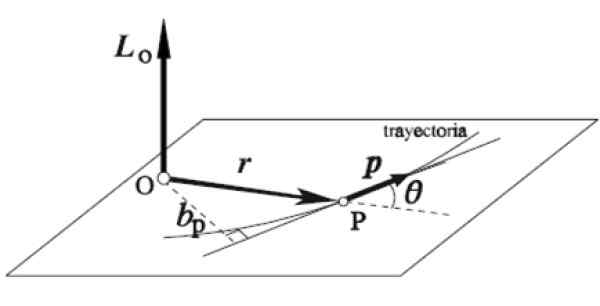Figuur 5. De hoekige vector. Bron: Wikimedia Commons.

Opdrachten

Oefening 1

De spin van figuur 6 gaat snel met hoeksnelheid Ω en de symmetrieas brak langzamer rond de verticale as Z. Deze beweging wordt genoemd precessie. Beschrijf de krachten die op de spin werken en het effect dat ze produceren.

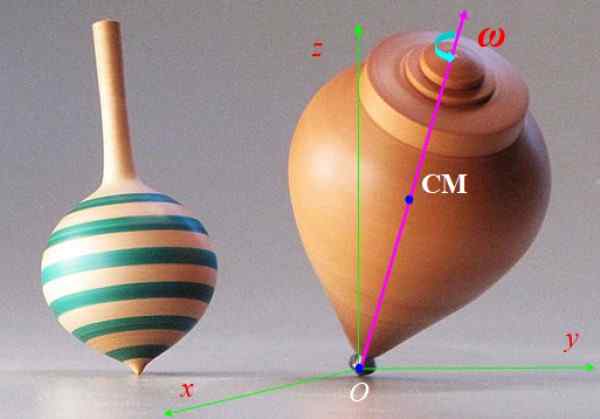Figuur 6. Spin -spin. Bron: Wikimedia Commons.

Oplossing

De krachten die op de spin werken, zijn normaal N, toegepast op het ondersteuningspunt met de grond of meer het gewicht mG, toegepast in het centrum van massa cm, met G De ernstversnellingsvector, verticaal gericht (zie figuur 7).

Beide krachten zijn evenwichtig, daarom beweegt de spin niet. Het gewicht produceert echter een koppel of koppel τ Net over het punt of, gegeven door:

τ_OF = R_OF X F, met F = MG.

Als R en MG Ze zitten altijd in het vlak terwijl de spin draait, volgens de regel van de rechterhand het koppel τ_OF Het bevindt zich altijd in het vliegtuig XY, loodrecht op beide a R als G.

Let daar op N produceert geen koppel ten opzichte van O, omdat de vector R Wat betreft of is NULL. Dat koppel produceert een verandering in het hoekmomentum dat de precessie van de spin rond de Z -as veroorzaakt.

Kan u van dienst zijn: thermodynamisch evenwicht: klassen en toepassingen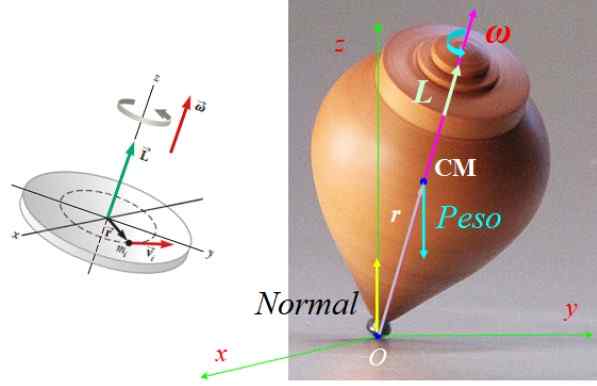Figuur 7. Krachten die op de spin en zijn hoekmomentum vector werken. Bron van de linker figuur: Serway, r. Natuurkunde voor wetenschap en engineering.

Oefening 2

Wijs op de richting en richting van de hoekmomentumvector L van de Trumpe van figuur 6.

Oplossing

Elk punt van de spin heeft massa m_Je, snelheid v_Je en positievector R_Je, Wanneer het draait om de Z -as. Het hoekmomentum L_Je van het deeltje is:

L_Je = R_Je X P_Je = R_Je X M_Jev_Je

Gezien R_Je En v_Je Ze staan ​​loodrecht, de omvang van L is:

L_Je = m_JeR_Jev_Je

De lineaire snelheid v is gerelateerd aan hoeksnelheid Ω door:

v_Je = r_JeΩ

Daarom:

L_Je = m_JeR_Je (R_JeΩ) = m_JeR_Je²Ω

Het totale hoekmomentum van de trompo l is de som van het hoekmomentum van elk deeltje:

L = (∑M_JeR_Je² ) Ω

∑ M_JeR_Je²  Het is het moment van traagheid van de spin, dan:

L= IΩ

Daarom L En Ω Ze hebben dezelfde richting en betekenis, zoals weergegeven in figuur 7.