Correspondentieregel van een functie

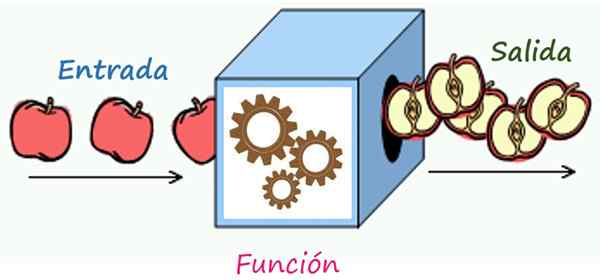
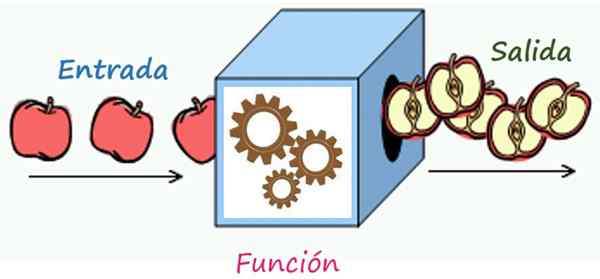De correspondentieregel is een mechanisme dat de elementen van de invoer in de uitvoerelementen transformeert. Bron: Wikimedia Commons/F. Zapata

Wat is de correspondentieregel van een functie?

De Correspondentieregel van een functie Wijzen op de manier waarop de elementen van de ene set gerelateerd zijn aan de elementen van de andere. De elementen van de eerste set staan ​​bekend als de domein, en voor die van de tweede, zoals de Codominium of contradominium.

De relatie of link tussen sets kan worden gespecificeerd door verbale of schriftelijke instructie, maar wanneer de sets numeriek zijn, wordt de correspondentieregel aangegeven door een formule.

Deze formule bevat de bewerkingen die moeten worden gedaan met de elementen van de startassemblage, en dus een reeks elementen verkrijgen die in het Codominium zijn opgenomen.

Wanneer de relatie tussen de elementen een functie is, voldoet de correspondentieregel aan twee speciale voorwaarden:

• Aan elk van de elementen van het domein wordt geassocieerd, door de correspondentieregel, een enkel element van het codominium, bekend als de afbeelding.
• Deze afbeelding is uniek, met andere woorden, geen element van het domein is geassocieerd met meer dan één element van codominium.

Op deze manier kunt u zich de correspondentieregel van een functie voorstellen als een mechanisme dat in een doos is vergrendeld. Elke domeinwaarde, zonder uitzondering, kan het vak binnenkomen en eruit komen, getransformeerd, via de bewerkingen aangegeven door de correspondentieregel. De voorbeelden zullen onmiddellijk worden gezien.

Voorbeelden

voorbeeld 1

De correspondentieregel van een functie kan worden uitgedrukt als een schriftelijke instructie, wanneer de elementen niet numeriek zijn.

Er is bijvoorbeeld een aantal landen, aangeduid als P, en een andere set steden C:

Het kan u van dienst zijn: u -test van Mann - Whitney: wat is het en wanneer toegepast, uitvoering, voorbeeld

P = Canada, Mexico, Spanje, VS, Frankrijk, Argentinië, Brazilië, Duitsland

C = Paris, London, Buenos Aires, Berlijn, Mexico City, Ottawa, Río, New York, Madrid, Washington, Bern, Rome, Brasilia, Toronto

Wees de correspondentieregel F Tussen P en C gegeven door:

F: P → C

Waar F Het is de regel "... wiens kapitaal is .. ”, Dat elk land associeert in P (de startset), met zijn hoofdstad in C (de aankomstset).

Bijvoorbeeld: “Spanje, wiens kapitaal is Madrid". Het "Spanje" -element behoort tot de start -p -set en het "Madrid" -element van de hele C, de aankomst.

De weergave van deze functie kan worden uitgevoerd via een Venn -diagram of gewoon via geordende paren.

Bestelde paren bevatten, zoals de naam al aangeeft, twee elementen met een specifieke volgorde, in dit voorbeeld is het eerste element van het paar het land, en de tweede, de hoofdstad.

Van zijn kant is het Venn -diagram een ​​manier om de functie te visualiseren, met de start- en aankomstsets, evenals de correspondentieregel daartussen.

Weergave van f als geordende paren

F = (Canada, Ottawa); (Mexico, Mexico City); (Spanje Madrid); (VS; Washington); (Parijs, Frankrijk); (Argentinië Buenos Aires); (Brazilië Brasilia); (Duitsland, Berlijn)

Het eerste paar associeert Canada, wiens kapitaal is Ottawa, The Second Associates Mexico, wiens kapitaal is Mexico -stad enzovoort.

Weergave van F als een Venn -diagram

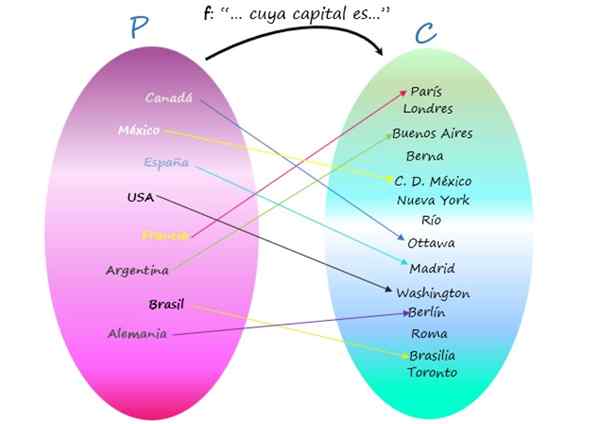
Merk op dat er steden zijn die niet de hoofdstad van enig land zijn, omdat, hoewel ze elementen van het codominium zijn, ze geen beeld zijn van enig element van de startset. Toch is de relatie een functie, omdat het belangrijkste is dat elk land zijn kapitaal heeft, en dit is uniek.

Kan u van dienst zijn: gebied van een gewone en onregelmatige Pentagon: hoe het wordt genomen, oefeningen

De subset gevormd door de elementen van het codominium die een beeld zijn van een bepaald element van het domein, wordt genoemd bereik of functie van de functie. Voor het voorbeeld, de route r van F is:

R = Paris, Buenos Aires, Mexico City, Ottawa, Madrid, Berlijn, Washington, Brasilia

Het is de moeite waard om te vragen of een relatie tussen C en P kan worden vastgesteld, waarbij C de startset wordt en de aankomst. Het antwoord is ja, maar het zou geen functie zijn, omdat er steden zijn die geen hoofdsteden zijn, zoals New York, of het land waarvan ze kapitaal zijn, verschijnt niet tussen de elementen van het P -complex, zoals Rome.

Voorbeeld 2

Wanneer de vertrekset en de aankomstset numeriek zijn, is de regel van correspondentie van de functie die ze verbindt een formule. Wees bijvoorbeeld de beheersing van een functie, de volgende set:

D = 0, 1, 2, 3, 4, 5, 6)

De correspondentieregel F: D → R die de elementen van D koppelt aan de set reële getallen R is:

F: "Double"

Als "x" een element is van de startset, is f (x) het overeenkomstige element van de aankomstset en is de correspondentieregel als volgt geschreven:

f (x) = 2x

Codominium is de reeks reële getallen. Een subset van de reais is de route van deze functie, de reeks getallen waarvan de waarde twee keer zo x is:

R = 0, 2, 4, 6, 8, 10, 12

In de vorm van geordende paren resulteert de correspondentieregel in:

F = (0.0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Bestelde paren kunnen worden grafisch in het Cartesiaanse vlak. Het eerste element van het koppel wordt op de horizontale as geplaatst, ook wel de as van de abscisas of "x" as genoemd, terwijl de tweede op de verticale as, as van de geordende of eenvoudig as "y" gaat:

Kan u van dienst zijn: distributieve eigendom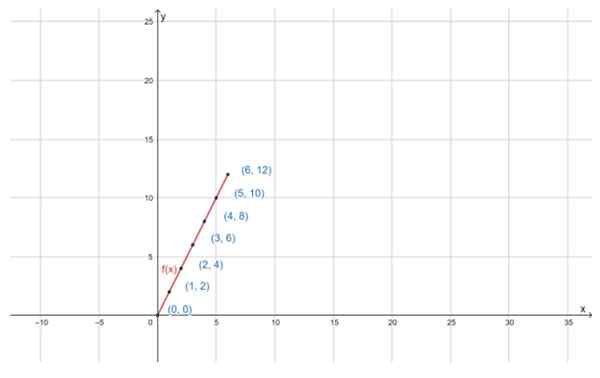 De grafiek van de functie f (x) = 2x, voor het opgegeven D -domein, is een rechte lijn. Bron: f. Zapata door Geogebra

Opdrachten

Bepaal de correspondentieregel voor de volgende relaties, wat aangeeft of ze al dan niet functies zijn. De reeks natuurlijke nummers is n en die van het echte is r.

Geef ook het domein, codominium en de route van de functie aan, in de gevallen waarin het overeenkomt:

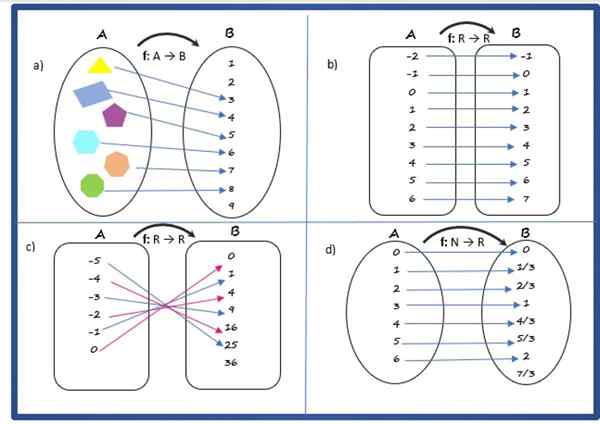
Oplossing voor

Het is een functie, omdat elk element van de startset, bestaande uit polygonen, een uniek beeld heeft in de aankomstset.

De correspondentieregel relateert de polygoon aan het aantal zijden, het domein bestaat uit set A van de polygonen:

A = driehoek, vierhoek, Pentagon, zeshoek, heptagon, octagon

Codominium is de set van de eerste natuurlijke nummers, waaronder 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

En de CO C zijn de natuurlijke getallen van 3 tot 8:

C = 3, 4, 5, 6, 7, 8

Oplossing B

Het is een functie, omdat het voldoet aan de hierboven gespecificeerde voorwaarden.

De correspondentieregel is:

f (x) = x + 1

De correspondentieregel geeft aan dat de functie wordt gedefinieerd door R → R, daarom is het domein de set reële getallen. En het co -oominium en de route vallen ook samen met het echte.

Oplossing C

Het is een functie, met de correspondentieregel:

f (x) = x²

Domein en codominium zijn een reeks van REA's, maar de route bestaat alleen uit positieve reële getallen, aangeduid als r⁺ en inclusief 0.

Oplossing D

Het is een functie. De correspondentieregel is:

f (x) = x/3

Het domein is de reeks natuurlijke getallen N en Codominium, evenals de route, zijn de echte n nummers R.