Bravais Networks Concept, kenmerken, voorbeelden, oefeningen

De Bravais -netwerken Ze zijn de set van veertien drie -dimensionale eenheidscellen waarin de atomen van een kristal. Deze cellen bestaan ​​uit een drie -dimensionale opstelling van punten die een basisstructuur vormen die periodiek wordt herhaald in de drie ruimtelijke richtingen.

De oorsprong van deze denominatie voor basic kristallijne structuren komt uit 1850, toen Auguste Bravais aantoonde dat er slechts 14 mogelijke basiscellen met drie dimensionale eenheid zijn mogelijk.

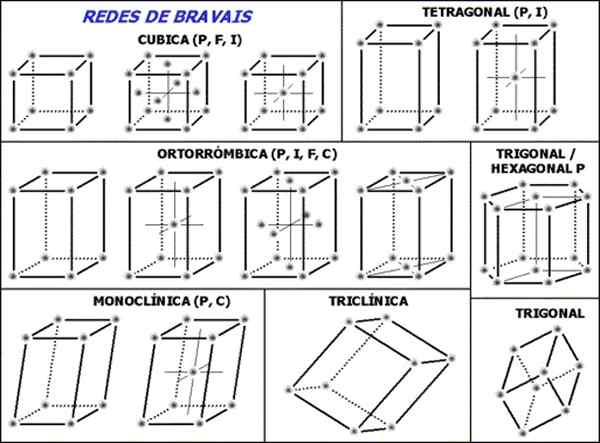
Figuur 1. Bravais -netwerken zijn de set van de 14 noodzakelijke en voldoende eenheidscellen om elke kristallijne structuur te beschrijven. (Wikimedia Commons)

De set van de 14 Bravais -netwerken is onderverdeeld in zeven groepen of structuren volgens de geometrie van de cellen, deze zeven groepen zijn:

1- kubiek

2- Tetragonaal

3- Ortorrombic

4- trigonaal-hexagonaal

5- Monokliniek

6- triclinic

7- Trigonaal

Elk van deze structuur definieert een eenheidscel, dit is het kleinste deel dat de geometrische opstelling van atomen in het glas behoudt.

[TOC]

Kenmerken van Bravais -netwerken

De veertien netten van Bravais, zoals hierboven vermeld, zijn onderverdeeld in zeven groepen. Maar elk van deze groepen heeft zijn eenheidscellen met zijn karakteristieke parameters die zijn:

1- De netwerkparameter (A, B, C)

2- Aantal atomen per cel

3- Relatie tussen netwerkparameter en atomaire radio

4- Coördinatienummer

5- Verpakkingsfactor

6- Interstitiële ruimtes

7- door vertalingen langs vectoren A, B, C De kristallijne structuur wordt herhaald.

Kubieke netwerken

Het bestaat uit het eenvoudige of kubieke kubieke netwerk, het kubieke netwerk gericht op gezichten of kubieke netwerk F en het kubieke netwerk gericht op de kubieke body of netwerk.

Alle kubieke netwerken hebben de drie Netwerkparameters overeenkomend met de X, Y -adressen, z van dezelfde waarde:

A = B = C

Cubic Network P

Het is handig om te benadrukken dat atomen worden weergegeven door bollen waarvan de centra zich in de hoekpunten van de kubieke cel P bevinden.

Kan u van dienst zijn: kunstmatige satellieten

In het geval van het kubieke netwerk p de Aantal atomen per cel Het is 1, omdat in elk hoekpunt alleen het achtste deel van het atoom zich in de eenheidscel bevindt, dan 8*⅛ = 1.

Hij Coördinatiegetal Geeft het aantal atomen aan dat nabijgelegen buren in het kristallijne netwerk zijn. In het geval van het kubieke netwerk P is het coördinatienummer 6.

Cubic Network I

In dit type netwerk Naast de atomen in de hoekpunten van de kubus is er een atoom in het midden van de kubus. Dus Atoomnummer per cel Unitaire in het kubieke netwerk P is 2 atomen.

Figuur 2. Body -gecentreerd kubisch netwerk.

Cubic Network F

Het is het kubieke netwerk dat naast de atomen in de hoekpunten een atoom in het midden van het gezicht van elke kubus heeft. Hij Aantal atomen per cel Het is 4, omdat elk van de zes atomen van het gezicht de helft in de cel heeft om 6*½ = 3 plus 8*⅛ = 1 in de hoekpunten te zeggen.

figuur 3. Kubiek netwerk gericht op gezichten.

Zeshoekig netwerk

In dit geval is de eenheidscel een rechte zeshoekige prisma. Zeshoekige netwerken hebben de drie Netwerkparameters Correspondering van de volgende relatie vervullen:

A = b ≠ c

De hoek zijn tussen vector A en B van 120º, zoals getoond in de figuur. Terwijl tussen vectoren A en C, evenals tussen B en C zijn rechte hoeken.

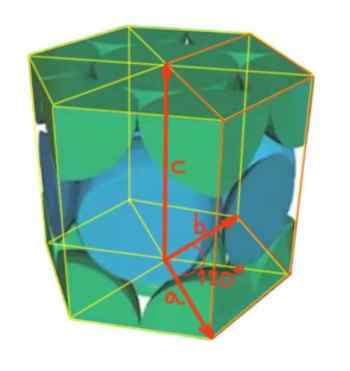Figuur 4. Zeshoekig netwerk.

Hij Aantal atomen per cel Het wordt als volgt berekend:

- In elk van de 2 bases van het zeshoekige prisma zijn er 6 atomen in de zes hoekpunten. Elk van deze atomen bezet ⅙ van de eenheidscel.

- In het midden van elk van de 2 zeshoekige bases is er 1 atoom dat 1/2 unitaire cel bezet.

- Op de 6 laterale gezichten van het zeshoekige prisma zijn er 3 atomen die elk van de eenheidscel bezetten, en 3 atomen die elk volume van de eenheidscel bezetten.

Het kan je van dienst zijn: hoor kracht: oppervlakte- en massakrachten

(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6 

De relatie tussen netwerkparameters A en B met de atomaire straal R in de veronderstelling dat alle atomen van gelijke radio zijn en in contact zijn is: 

a/r = b/r = 2

Voorbeelden

Metalen zijn de belangrijkste voorbeelden van kristallijne structuren en ook de eenvoudigste omdat ze over het algemeen bestaan ​​uit een enkel type atoom. Maar er zijn andere niet -metalen verbindingen die ook kristallijne structuren vormen, zoals diamant, kwarts en vele andere.

- Het ijzer

IJzer heeft een eenvoudige kubieke eenheidscel met netwerkparameter of rand A = 0,297 nm. In 1 mm zijn er 3,48 x 10^6 eenheidscellen.

- Koper

Het heeft een kubieke kristallijne structuur gecentreerd op gezichten, alleen gevormd door koperatomen.

- Kostbare edelstenen

Kostbare edelstenen zijn kristallijne structuren in principe dezelfde verbinding, maar met kleine delen van onzuiverheden die vaak verantwoordelijk zijn voor de kleur ervan.

Diamant

Het is alleen samengesteld uit koolstof en bevat geen onzuiverheden, daarom mist het kleur. De diamant heeft Kubieke kristallijne structuur (isometrisch-hexoctahedral) en is het moeilijkst bekende materiaal.

Kwarts

Het is samengesteld uit silica -oxide, het is meestal kleurloos of wit. De kristallijne structuur is Trigonal-trapezoédrica.

Robijn 

Het bestaat uit aluminiumoxide met chroomonzuiverheden die het zijn karakteristieke rode kleur geven. Vormt één Zeshoekig kristallijn netwerk.

Saffier 

Het is ook een aluminiumoxidekristal, maar met onzuiverheden van titanium en ijzer, die verantwoordelijk zijn voor hun blauwe kleur in verschillende tinten. Zoals de ruby ​​heeft zeshoekige structuur.

Jade

Kostbare steen over het algemeen groen, heeft Monoklinische structuur En het is samengesteld uit silicaat van ijzer-magnesium-calcio.

Topaas 

Het is kleurloos met een Ortorrombische structuur van aluminium-hydroxide-silicaat fluoride.

Opgeloste oefeningen

Oefening 1

Zoek de relatie tussen de netwerkparameter en de atomaire straal voor een kubisch netwerk F.

Het kan u van dienst zijn: theorie van de oerknal: kenmerken, fasen, bewijs, problemen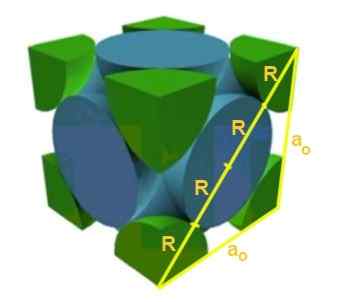

Oplossing: In de eerste plaats wordt aangenomen dat atomen worden weergegeven als bollen alle straal R in "contact" met elkaar, zoals weergegeven in de figuur. Er wordt een rechthoekige driehoek gevormd waarin wordt vervuld dat:

(4 r)^2 = a^2 + a^2 = 2 a^2

Dus je hebt dat de rand-radio-relatie is:

A/R = 4/√2

Oefening 2

Zoek de relatie tussen de netwerkparameter en de atomaire straal voor een kubisch netwerk I (body gecentreerd).

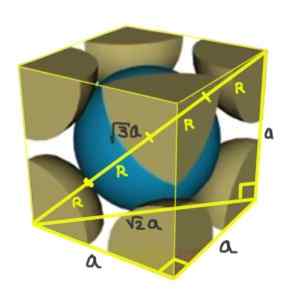
Oplossing: Atomen worden verondersteld te worden weergegeven als alle Radius R -bollen in "contact" met elkaar, zoals weergegeven in de figuur.

Twee rechthoeken worden gevormd een van hypotenusa √2a en de andere van hypotenuse √3a zoals kan worden aangetoond met behulp van de Pythagorische stelling. Van daaruit moet u een relatie tussen de netwerkparameter en de atomaire straal voor een kubisch netwerk I (gecentreerd in het lichaam) zijn::

A/R = 4/√3

Oefening 3

Zoek de verpakkingsfactor F voor een eenheidscel van een kubieke structuur F (kubiek gecentreerd op gezichten) waarin atomen radio R hebben en in "contact" zijn.

Oplossing: De verpakkingsfactor F wordt gedefinieerd als de verhouding tussen het volume dat wordt bezet door de atomen in de eenheidscel en het volume van de cel:

F = Vatomen / Vcel

Zoals hierboven aangetoond, is het aantal atomen per eenheidscel van een kubisch netwerk dat op gezichten is gecentreerd 4, dus de verpakkingsfactor zal zijn:

F = 4 [4πr^3/3] /[A^3] = ..

… 4 [4πr^3/3]/[4r/√2]^3 = (√2) π/6 = 0,74

Referenties

1. Crystal Structures Academic Resource Center. [PDF]. Ontvangen op 24 mei 2018, van: Web.IIT.Edu
2. Kristallen. Ontvangen op 26 mei 2018, van: Thoughtco.com
3. Persboeken. 10.6 Latice -structuren in kristallijne vaste stoffen. Ontvangen op 26 mei 2018, van: OpenTextbc.AC
4. Ming. (30 juni 2015). Types kristalstructuren. Ontvangen op 26 mei 2018, van: CrystalVisions-Film.com
5. Helmestine, Anne Marie, pH.D. (31 januari 2018). Types van 
6. Kittel Charles (2013) Solid State Physics, Condensed Matter Physics (8e editie). Wiley.
7. Khi. (2007). Kristallijne structuren. Ontvangen op 26 mei 2018, van: folk.Ntnu.Nee
8. Wikipedia. Bravais Latices. Opgehaald uit: in.Wikipedia.com.