Tweede regels

Het hout van de deur van deze tuin is zo bereid dat ze droge lijnen bepalen. Bron: f. Zapata. Pxheren.com

Wat zijn de droge lijnen?

In het vliegtuig, de Tweede regels Het zijn die die andere lijnen en bochten kruisen. In het geval van twee lijnen is de kruising ervan een punt, terwijl de Secant -lijn bij een curve dit in twee of meer punten snijdt.

Observeer het hek van de bovenste figuur zorgvuldig. Daarop zijn verschillende rechte rechte kleuren getekend, aangeduid als l₁, L₂ en ik₃. De pijlen aan beide kanten betekenen dat de lijnen voor onbepaalde tijd worden verlengd.

Nou, de lijnen l₁, L₂ en ik₃ Ze drogen elkaar, omdat elk paar op paarse punten wordt gesneden.

Bovendien zijn de lijnen L₁ en ik₂, Zoals l₁ en ik₃, Ze bepalen 4 hoeken met elkaar, twee van hen acuut en de andere stompe, terwijl de lijnen L₂ en ik₃ Ze staan ​​loodrecht, wat betekent dat de 4 hoeken die ze hebben bepaald, recht zijn.

Twee parallelle lijnen kunnen nooit droog zijn, omdat ze vanwege hun toestand geen toevalpunten hebben. Op zijn beurt zijn de samenvallende lijnen niet droog, omdat ze meer dan één punt gemeen hebben.

Kenmerken van de drooglijnen

• Twee Secant -lijnen hebben een uniek punt als kruising.
• De hellingen van twee drooglijnen moeten anders zijn. Ja m₁ Het is de helling van de lijn l₁, en M₂ Het is de helling van de lijn l₂, dan is het vervuld dat m₁ ≠ M₂.
• De hellingen van twee drooglijnen loodrecht op elkaar, waarvan de respectieve hellingen m zijn₁ en M₂, Ze vervullen de relatie m₁ = -1/ m₂. Bovendien is het scalaire product tussen twee vectoren v En of In deze lijnen is nul, omdat de definitie van scalair product is v of = V ∙ u ∙ cos θ, zijnde θ de hoek tussen de vectoren.
• Een lijn kan scheiden zijn van een curve of een andere geometrische figuur.
• Bij het kruisen genereren twee drooglijnen 4 hoeken, identiek twee tot twee of identiek aan elkaar.

Kan u van dienst zijn: fractionele vergelijkingen

Hoe te weten of twee lijnen droog zijn

Uit de kenmerken van de hierboven beschreven drooglijnen is het mogelijk om drie criteria vast te stellen om te weten of twee lijnen droog zijn:

-De hellingen vergelijken. Als deze verschillen, zijn de lijnen droog.

-Het uitvoeren van het scalaire product tussen twee vectoren die in deze lijnen zijn opgenomen, genaamd Bestuurders. Als het scalaire product nietig is, zijn de lijnen droog en loodrecht, en als het niet -nul is, is het mogelijk om de minimale hoek ertussen te weten, wat de acute hoek is die tussen de lijnen bestaat.

Op voorwaarde dat deze hoek verschilt van 0º, zijn de lijnen droog en als deze gelijk is aan 0º, dan zijn het parallelle lijnen.

-Direct berekenen van de acute hoek die tussen de lijnen bestaat, hun hellingen bekend. Dit kan worden gedaan door de formule die de raaklijn van de genoemde hoek met de hellingen relateert.

Laat m₁ en M₂ de hellingen, en θ de acute hoek ertussen. De raaklijn van θ wordt gegeven door:

Soorten droogleidingen

Wanneer twee lijnen elkaar drogen, kunnen ze de volgende typen zijn:

• Schuin, Als ze bij sneden twee acute hoeken en twee stompe hoeken vormen. Deze hoeken zijn aanvullend, dat wil zeggen de som van de maat van de hoek plus de een van de stompe hoek is gelijk aan 180º. In totaal is de som van de 4 hoeken gelijk aan 360º.
• Loodrecht, Degenen die 4 hoeken kruisen die gelijk zijn aan 90º.

Hoe u de kruising tussen twee lijnen kunt vinden

Als twee lijnen aan het drogen zijn, hebben ze slechts één snijpunt, dat het systeem van twee lineaire vergelijkingen oplost met twee onbekenden. Als de lijnen in het algemeen worden gegeven: Ax + by = c, is het systeem van vergelijkingen:

Kan u van dienst zijn: oneindige set: eigenschappen, voorbeelden

naar₁X + B₁ y = c₁

naar₂X + B₂ y = c₂

Hoe u de kruising tussen een lijn en een curve kunt vinden

Het kennen van de vergelijkingen van zowel de lijn als de curve wordt het systeem van vergelijkingen voorgesteld en wiens oplossingen overeenkomen met het snijpuntspunten. Als het systeem een ​​oplossing mist, is de lijn niet scheiden van de curve, noch is het als er een enkel snijpunt is, omdat de lijn in dat geval de linie raakt aan de curve.

Om de lijn te drogen, zoals in het begin vermeld, moet het systeem van vergelijkingen twee of meer oplossingen hebben.

Voorbeelden van droogleidingen

Het Cartesiaanse vlak

Het Cartesiaanse vlak wordt bepaald door twee lijnen, genoemd X Axis En As y, respectievelijk horizontaal en verticaal. Deze lijnen staan ​​loodrecht en hun snijpunt wordt genoemd Oorsprong van het coördinatensysteem, of gewoon oorsprong.

De diagonaal van een polygoon

Een polygoon is een platte figuur van drie of meer kanten, die samenvoegen in punten die hoekpunten worden genoemd. Een segment dat zich bij twee niet -opeenvolgende hoekpunten verbindt, is een diagonaal van de polygoon, en de lijn die dit segment bevat is secant op de betreffende polygoon.

Een omtrek touw

Het touw van een omtrek is het segment dat twee van zijn punten verbindt. Het hoofdtouw is de diameter, die noodzakelijkerwijs door het midden van de omtrek gaat. Welnu, de lijn die elk touw bevat, inclusief de diameter, is een drooglijn naar de omtrek.

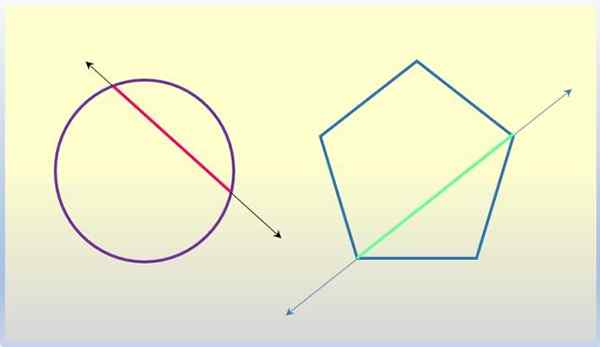Tweede regels voor geometrische figuren. Bron: f. Zapata.

De dwarssleutel

Met dit gereedschap worden de moeren die de banden aan de wielen van de voertuigen houden, los. De armen vormen lijnen die droog zijn en tegelijkertijd loodrecht.

Kan u van dienst zijn: proportionele variatie

Alfabet teksten

Sommige alfabetletters bestaan ​​uit rechte beroertes die Secant bepalen. Letter X bestaat bijvoorbeeld uit twee slagen die op één punt worden gesneden en de letter T bestaat uit twee loodrechte lijnen.

Opgeloste oefeningen

Oefening 1

Bepaal of de lijnen gegeven door:

L₁ : y = 5x - 3

L₂ : y = -2x+1

Oplossing

De helling van een lijn gegeven in de vorm y = mx + b is de waarde van m, dat wil zeggen de coëfficiënt die bij de x hoort. Sinds m₁ = 5 en m₂ = -2, die anders zijn, wordt geconcludeerd dat de lijnen droog zijn.

Oefening 2

Wat is de acute hoek tussen de lijnen van oefening 1?

Oplossing

De M -waarden worden direct vervangen₁ = 5 en m₂ = -2 in de formule gegeven in de voorgaande secties:

Daarom is de hoek tussen de lijnen θ = arctg 0.777… = 37.9º.

Oefening 3

Wat is de kruising tussen de lijnen van de vorige oefeningen?

Oplossing

Het systeem van vergelijkingen wordt als volgt voorgesteld:

Wiens oplossing is: x = 4/7; y = -1/7 (kan worden opgelost door een van de resolutiemethoden voor vergelijkingssystemen, of met een rekenmachine).

Daarom is het punt van snijpunt van lijnen: P (4/7; -1/7).

Referenties

1. Analytische meetkunde.Info. Tweede regels. Hersteld van: geometriaaalitics.Info.
2. Larson, r. 2006. Berekening met analytische geometrie. 8e. Editie. McGraw Hill.
3. Lijnen die kruisen. Hersteld van: TeacheralTuna.com.
4. Eisen, b. Tweede regels. Hersteld van: UniversOFormulas.com.
5. Villena, m. Analytische geometrie in R3. Opgehaald uit: DSPACE.Espol.Edu.EC.