Inductieve reactantie

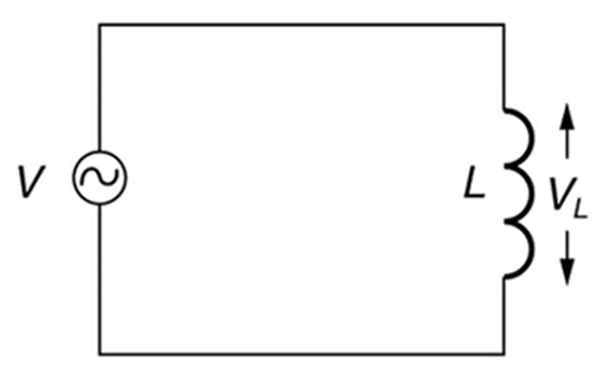
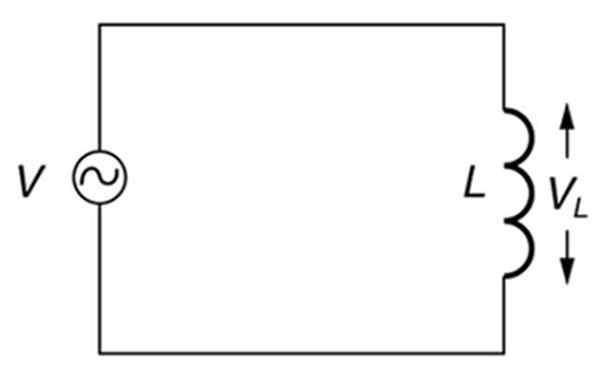Een puur inductief alternatief circuit. Bron: Open Stax. College natuurkunde.

Wat is inductieve reactantie?

De Inductieve reactantie Het verwijst naar de door de spoel gepresenteerde oppositie naar de doorgang van de stroom, in een alternatief circuit. Met andere woorden, het is het vermogen van de inductor om de stroom in een alternatief circuit te verminderen. Aangeduid als x_L, De waarde ervan hangt af van de inductie en de hoekfrequentie van de spanning:

X_L= Ω ∙ l

Waarbij ω de hoekfrequentie is in radialen/s en L -inductie, gemeten in Henrios (H) in het internationale systeem van eenheden als.

Grote inductanties produceren grote inductieve reactantie, omdat hun weerstand tegen verandering groter is. En de reactantie neemt ook toe met de frequentie, dus een bepaalde inductie L zal een grotere reactantie veroorzaken, hoe hoger de spanningsfrequentie.

De inductieve reactantie -eenheid is de ohmio, gesymboliseerd door ω. Het is dezelfde eenheid van elektrische weerstand, maar anders dan dit, x_L Het is niet constant, omdat het afhangt van de frequentie van de toegepaste alternatieve spanning.

Daarom, in een circuit waarvan de enige elementen een alternatieve bron en een inductie (inductief circuit) zijn, zoals die in de bovenstaande figuur, zal de inductieve reactantie afhangen van de frequentie van de bron.

X's analogie echter_L Met elektrische weerstand kan het worden uitgebreid tot het inductieve circuit, waardoor de wet van Ohm de toepassing kan zijn. Als X is gedefinieerd_L Als de verhouding tussen spanningsamplitudes v_L In de inductor en de huidige i_L Dat kruist het:

X_L = V_L / Yo_L

Je kunt de OHM -wet als volgt schrijven voor puur inductieve circuits:

V_L = X_L∙ I_L

Inductieve reactantie -formules

Om de inductieve reactantie te berekenen, wordt de in het begin gegeven formule gebruikt, waarbij L inductantie vertegenwoordigt (Henrios) en ω de hoekfrequentie (radialen/seconde):

Kan u van dienst zijn: Millikan Experiment: procedure, uitleg, belang

X_L= Ω ∙ l

Het is gebruikelijk dat de frequentie wordt uitgedrukt in Hertz of Hertzio (Hz). In dit geval wordt het aangegeven door F en is het gerelateerd aan de hoekfrequentie door de formule:

Ω = 2π ∙ f

In dit geval wordt de reactantie berekend als:

X_L= 2πf ∙ l

In een van deze formules resulteert de inductieve reactantie in ohm, zoals eerder uitgelegd.

Het effect van inductie op een inductief circuit

Omdat de inductie tegen de veranderingen of variaties van de stroom is, wordt de inductieve reactantie gekenmerkt door de stroomgolf uit te stellen ten opzichte van de spanningsgolf.

In de volgende grafiek, die spanning V toont_L (Blauw) en de huidige i_L (rood) In de inductor, beide sinoidaal, wordt waargenomen dat beide golven verouderd zijn 90º. Beginnend bij t = 0 is de spanningswaarde maximaal, maar de stroom is op dat moment nul.

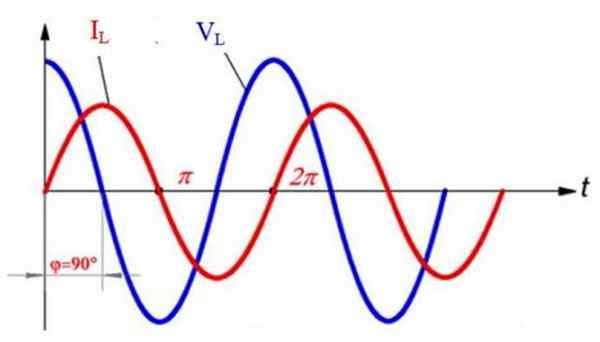Wisselstroom en spanning in een inductief circuit. Voorbereid door: f. Zapata.

Later wordt opgemerkt dat de stroom zijn maximale waarde bereikt op t = π /2, maar tegen die tijd wordt de spanning geannuleerd en investeert de polariteit, dat wil zeggen dat het negatief wordt. Tegelijkertijd verlaagt de stroom zijn waarde, terwijl de spanning steeds negatiever wordt.

Vervolgens bereikt de spanning bij t = π zijn maximale grootte, hoewel met de omgekeerde polariteit, en vervolgens wordt de stroom geannuleerd. Uit dit alles volgt dat wanneer V_L Het bereikt een piek, de stroom wordt geannuleerd en elke keer dat de stroom zijn maximale grootte bereikt, is de spanning 0.

De stroom bereikt altijd zijn piek nadat de spanning dat wel doet, en dit komt omdat, zoals in het begin vermeld, inductie tegen toenemen of afneemt.

Kan u van dienst zijn: mechanisch voordeel: formule, vergelijkingen, berekening en voorbeelden

Hoe de inductieve reactantie te berekenen

Het berekenen van de inductieve reactantie is heel eenvoudig: het is noodzakelijk om de waarde van de inductantie en de frequentie van de toegepaste alternatieve spanning te kennen. Vervolgens worden deze gegevens vervangen in een van de formules die in de voorgaande sectie worden gegeven en wordt de overeenkomstige bewerking uitgevoerd.

De volgende voorbeelden en opgeloste oefeningen laten zien hoe het in verschillende situaties te doen.

Voorbeelden

voorbeeld 1

Stel dat een L = 5 MH -inductor, waarop een alternatieve frequentiespanning wordt toegepast 60.0 Hz. De inductieve reactantie in dit geval wordt berekend door:

X_L= 2πf ∙ l

Maar voordat de waarden worden vervangen, moet inductantie Henrios worden, zich vermenigvuldigen met de 1 × 10 -factor⁻³. Daarom:

L = 5 × 10⁻³ H

Dus:

X_L= 2πf ∙ l = x_L= 2π × 60 Hz × 5 × 10⁻³ H = 1. 88 ohm

Voorbeeld 2

Nu is dezelfde inductantie verbonden met een andere alternatieve frequentievoltage: 10.0 kHz. In dit geval presenteert inductie een grotere reactantie:

X_L= 2πf ∙ l = x_L= 2π × 10.0 × 10³ Hz × 5 × 10⁻³ H = 314.2 ohm

Voorbeeld 3

De spanning toegepast op de inductie van voorbeelden 1 en 2 heeft een waarde van 120 V rms. De respectieve RMS -stroom wordt bepaald door OHM V -wet_L = X_L∙ I_L:

Je_L = V_L / X_L

Voor de frequentie van 60.0 Hz, de stroom is:

Je_L = 120 V / 1. 88 ohm = 63.8 a

En voor de frequentie van 10.0 kHz:

Je_L = 120 V / 314.2 ohm = 0.38 a

Omdat in het laatste geval de reactantie veel groter is, wordt verwacht dat de stroom kleiner zal zijn. Deze eigenschap maakt de inductor een hoogfrequent filter, een functie die wordt gebruikt om hoogfrequente geluiden in geluidsapparatuur te verminderen, of om apparaten te beschermen tegen plotselinge huidige ups, naast andere toepassingen.

Kan u van dienst zijn: Steiner Theorem: uitleg, toepassingen, oefeningen

Opgeloste oefeningen

Oefening 1

Bepaal de inductieve reactantie in een circuit dat bestaat uit een inductie van 2.5 MH, in serie met een alternatieve spanningsbron, waarvan de frequentie 75 r is.P.M.

Oplossing

Een volledige revolutie of cyclus is gelijk aan 2π radialen, en een minuut heeft 60 seconden, daarom een ​​frequentie van 75 r.P.M is gelijk aan:

75 r.P.M = 75 × 2π radialen / 60 seconden = 7.85 radialen/s

En met deze waarde is de reactantie:

X_L= Ω ∙ l = (7.85 radialen/s) × 2.5 × 10⁻³ H = 0.02 Ω

Oefening 2

Seriële inductantie wordt gebruikt met de bron van een computer om de ruis uit hoge frequenties te filteren.

a) Wat zou de minimale inductiewaarde moeten zijn die nodig is om een ​​2 kΩ -reactantie te produceren, als de frequentie van het signaal dat moet worden filteren 15 kHz is?

b) Vind de reactantie van deze inductor met de frequentie van 60 Hz.

Oplossing voor

X_L = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Daarom is het opruimen van vergelijking x_L= 2πf ∙ l, je hebt:

L = x_L / 2π ∙ f = 2000 Ω / 2π × 15000 Hz = 0.0212 h = 21.2 MH

Oplossing B

X opnieuw gebruiken_L= 2πf ∙ l, maar met F = 60 Hz, resultaten:

X_L= 2π × 60 Hz × 0.0212 H = 8 ohm.

Referenties

1. Bauer, W. (2011). Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill. 
2. Giancoli, D. (2006). Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
3.  Katz, D. (2013). Natuurkunde voor wetenschappers en ingenieurs. Stichtingen en verbindingen. Cengage leren.
4. Open Stax. College natuurkunde. Opgehaald uit: OpenStax.borg.
5. Sears, Z. (2016). Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 2. Pearson