Trigonometrische redenen voorbeelden, oefeningen en toepassingen

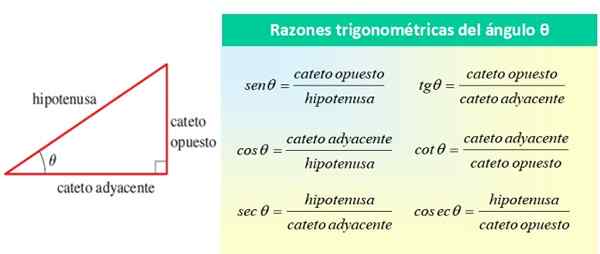
De trigonometrische redenen Het zijn de quotiënten of redenen die kunnen worden gedaan met de waarde van de zijkanten van een juiste driehoek. Deze zijden zijn: twee categorieën die 90º met elkaar vormen en de hypotenuse, die de acute hoek θ vormt met een van de categorieën.

6 quotiënten kunnen worden gevormd. Hun namen en respectieve afkortingen zijn:

• BREESE (SEN)
• Coseno (COS)
• raaklijn (tg of tan)
• Cotangent (CTG of COTAN)
• Secante (sec) en
• Harvester (harmonie)

Ze verwezen allemaal naar hoek θ, zoals getoond in de volgende figuur:

Figuur 1. De trigonometrische redenen van de acute hoek θ. Bron: f. Zapata.

De fundamentele trigonometrische redenen van hoek θ zijn sin θ, cos θ en tan θ, terwijl de resterende redenen kunnen worden uitgedrukt in termen van deze drie. Van de vorige foto kun je dat zien:

• Sec θ = 1/ cos θ
• schade θ = 1/ sin θ
• COT θ = 1/tg θ

De grootte van de zijkanten van de driehoek heeft geen invloed op de waarde van de redenen, omdat twee driehoeken waarvan de hoeken hetzelfde meten, vergelijkbare driehoeken zijn en de respectieve quotiënten tussen de zijden dezelfde waarde hebben.

[TOC]

Voorbeeld

Laten we bijvoorbeeld de trigonometrische redenen van hoek θ in de volgende driehoeken berekenen:

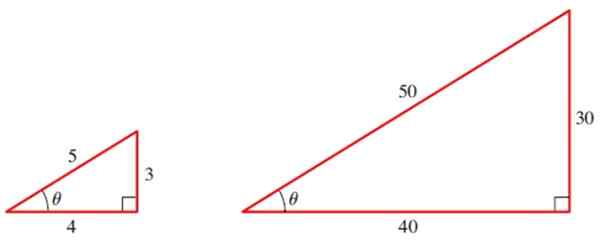Figuur 2. Twee vergelijkbare driehoeken hebben dezelfde trigonometrische redenen voor hun hoeken. Bron: Stewart, J.Precculment: wiskunde voor berekening.

Voor de kleine driehoek hebben we de drie basisredenen van de hoek θ:

sin θ = 3/5

cos θ = 4/5

tg θ = ¾

En laten we nu de drie basisredenen van θ berekenen met de grote driehoek:

sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

Tg θ = 30/40 = ¾

Een belangrijk detail om te overwegen is als volgt: zowel sin θ als cos θ zijn minder dan 1, omdat de categorieën altijd minder meten dan de hypotenuse. Inderdaad:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Opgeloste oefeningen

In de volgende oefeningen wordt gevraagd om de juiste driehoek op te lossen, wat betekent dat de lengte van zijn drie zijden en de maat van zijn interne hoeken het vinden.

Kan u van dienst zijn: Eerste -gradenvergelijkingen: formule, hoe ze op te lossen, bijvoorbeeld oefeningen

Pythagoras -stelling is van toepassing op rechthoekige driehoeken en is zeer nuttig wanneer twee van de zijden bekend zijn en de ontbrekende moet worden bepaald. De stelling zegt:

Hypotenuse² = tegenover Cateto² + aangrenzende cateto²

We kunnen de stelling van Pythagoras verifiëren met de kleine driehoek van figuur 2, waarvan de benen 3 en 4 zijn. De volgorde waarin de categorieën worden genomen, doet er niet toe. De stelling toepassen die we hebben:

Hypotenuse² = 3² + 4² = 9 + 16 = 25

Daarom is de hypotenuse:

Hypotenuse = √25 = 5

- Oefening 1

Bereken de trigonometrische redenen van de hoeken die in de volgende driehoeken worden getoond:

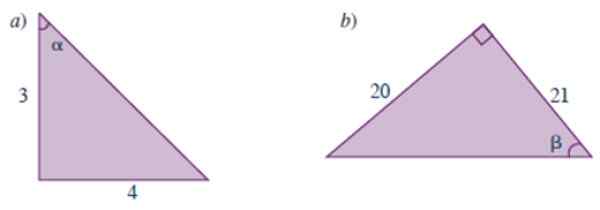figuur 3.- Driehoeken voor het jaar verdwenen 1. Bron: Carena, M. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding.

Oplossing voor

Deze driehoek is hetzelfde in figuur 3, maar ze vragen ons om de trigonometrische redenen van de andere acute hoek, aangeduid als a. De verklaring biedt echter niet de waarde van de hypotenusa, maar door toepassing van de stelling van Pythagoras weten we dat het 5 waard is.

De redenen kunnen rechtstreeks uit de definitie worden berekend, voorzichtig zijn bij het selecteren van het been dat het tegenovergestelde is van de hoek α om sen α te berekenen. Laten we eens kijken:

• sin α = 4/5
• cos α = 3/5
• Tg α = 4/3
• COT α = ¾
• Sec α = 1/(3/5) = 5/3
• schade α = 1/(4/5) = 5/4

En zoals we kunnen zien, zijn de waarden van trigonometrische redenen uitgewisseld. Inderdaad, α en θ zijn complementaire hoeken, wat betekent dat ze 90º toevoegen. In dit geval is het vervuld dat sen α = cos θ enzovoort om de andere redenen.

Oplossing B

Laten we de hypotenusa van de driehoek berekenen door de stelling van Pythagoras:

Hypotenuse² = 20² + eenentwintig² = 841

√841 = 29

Dan zijn de 6 trigonometrische redenen van hoek β:

• Sen β = 20/29
• cos β = 21/29
• TG β = 20/21
• COT β = 21/20
• SEC β = 1/(21/29) = 29/21
• schade β = 1/(20/29) = 20/29

Kan u van dienst zijn: gecombineerde bewerkingen

- Oefening 2

a) Zoek de waarde van X in de figuur.

b) Bereken de omtrek van de 3 getoonde driehoeken.

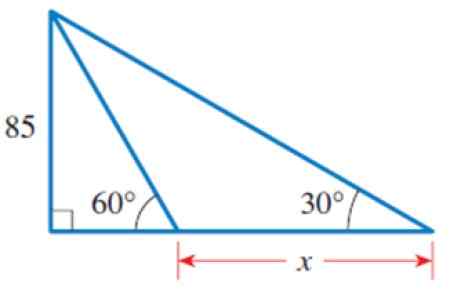Figuur 4. Driehoeken voor het jaar loste 2 op. Bron: Stewart, J. Precculment: wiskunde voor berekening.

Oplossing voor

In de figuur kunnen we verschillende driehoeken identificeren, in het bijzonder de rechthoekige driehoek van links, die een categorie heeft gelijk aan 85 en de acute hoek 60º.

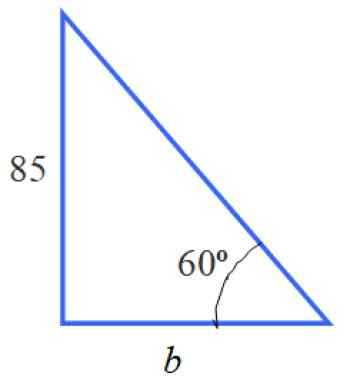Figuur 5. De driehoek aan de linkerkant.

Met de informatie van deze driehoek kunnen we zijde B berekenen. Het is niet de maatregel die de verklaring vraagt, maar het kennen van de waarde ervan is een vorige stap.

Om de juiste reden te bepalen is Tg 60 º = 85 /B, omdat B het been is dat grenst aan 60 ° is en 85 het tegenovergestelde is van die hoek. Daarom:

B = 85 / tg 60º = 85 / √3

Eenmaal bekend B, zullen we de grote en buitenste rechthoekige driehoek gebruiken, die een gemeenschappelijke kant heeft met de vorige driehoek: degene die 85 meet. Dit is de cateto tegenover de hoek van 30º.

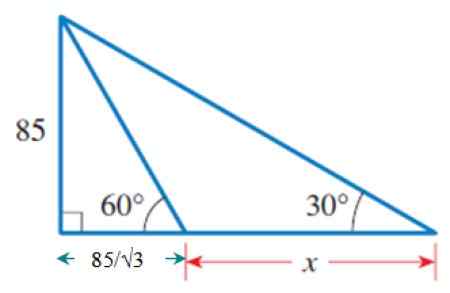Figuur 6. De buitenste driehoek, waarvan een deel van de basis al bekend is.

Vandaar:

Cateto grenzend aan 30º = (85/√3) + x

Nu kunnen we het volgende verhogen:

85 / [(85 / √3) + x] = Tg 30º

Wat zich in vierkante haakjes bevindt, vermenigvuldig de 30º TG:

85 = [(85/√3) + x]. TG 30º

De distributieve eigenschap van vermenigvuldiging toepassen:

85 = Tg 30º. (85/√3) + x. TG 30º

Daarom:

X.Tg 30º = 85 - Tg 30º. (85/√3) = 85 [1 - Tg 30º . (1/√3)] = 85 . (2/3) = 170/3

De Tg -waarde vervangen 30º = √3 / 3:

x = (170/3) ÷ (√3 / 3) = 98.vijftien

Oplossing B

Perimeter van de kleine driehoek

Zijn h₁ De hypotenusa van deze driehoek, die kan worden berekend door Pythagoras Stelling of via een trigonometrische reden, bijvoorbeeld Cos 60º:

cos 60 º = 85 / √3 / h₁→ h₁ = (85/√3) ÷ cos 60º = 98.1

Om P te vinden, de omtrek van deze driehoek, voegen we eenvoudig de 3 zijden toe:

Kan u van dienst zijn: beschrijvende statistieken: geschiedenis, kenmerken, voorbeelden, concepten

P = 85 + (85/√3) + 98.1 = 232.2

Perimeter van de externe driehoek

Zijn h₂ naar de hypotenusa van de externe driehoek:

Sen 30º = 85 ÷ h₂  

H₂ = 85 ÷ sin 30º = 170

Voor deze driehoek is de omtrek:

P = 85 + [(85/√3) + 98.15] + 170 = 402.22

Perimeter van de niet -rectangle driehoek

Vanuit deze driehoek kennen we al alle kanten:

P = x + h₁ + H₂ = 98.15 + 98.15 + 170 = 366.3

Toepassingen van trigonometrische redenen

Trigonometrische redenen hebben tal van praktische toepassingen, bijvoorbeeld hoogtes kunnen worden berekend.

Stel dat een watertoren op 325 voet van een gebouw ligt. Een waarnemer die zich in een venster bevindt, merkt op dat de hoogte van de bovenste uiteinde van de toren 39 º is, terwijl de depressiehoek waarmee de basis van de toren wordt gezien, 25º is. Wonderen:

a) Wat is de hoogte van de toren?

b) Hoeveel is het venster?

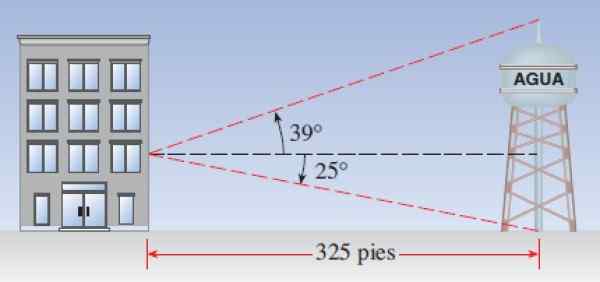Figuur 7. Schema om de hoogte van de Vista Torre uit een gebouw te berekenen. Bron: Stewart, J. Precculment: wiskunde voor berekening.

Oplossing voor

Van de cateto tegenover 39 van de bovenste driehoek krijgen we een deel van het antwoord:

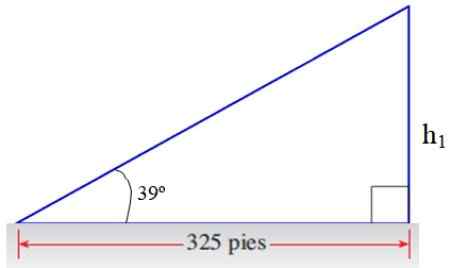Figuur 8. Driehoek voor toepassingsoefening. Bron: f. Zapata.

H₁/325 = Tg 39º → H₁ = 325 . Tg 39º voet = 263.2 voet

Op dezelfde manier krijgen we de rest van de hoogte van de toren, genaamd h₂ Van de onderste driehoek:

H₂/325 = Tg 25º → H₂ = 325 . Tg 25º voet = 151.6 voet

De totale hoogte van de toren is h₁ + H₂ = 263.2 + 151.6 voet = 414.7 voet.

Oplossing B

Het venster is precies op een hoogte h₂ grond:

H₂ = 151.6 voet.

Referenties

1. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding. Nationale Universiteit van de kust.
2. Hoffman, J. Selectie van wiskundeproblemen. Deel 3.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
5. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.