Vierkante wortel van 3 (eenvoudige oplossing en uitleg)

De vierkantswortel van 3 is 1.73205080756887.

Het kan worden uitgedrukt:

√3 = 1.73205080756887

Om te weten wat de 3 vierkante wortel, Het is belangrijk om de definitie van de vierkantswortel van een nummer te kennen. Gegeven een positief getal "a", is de vierkantswortel van "a", aangegeven door √a, een positief getal "b" zodat wanneer "b" erdoor wordt vermenigvuldigd, het resultaat "a" is.

De wiskundige definitie zegt: √a = b ja, en alleen als, b² = b*b = a. Daarom, om te weten wat de vierkantswortel van 3 is, dat wil zeggen de waarde van √3, moet een "b" -nummer worden gevonden dat b² = b*b = √3.

Bovendien is √3 een irrationeel getal, dat bestaat uit een oneindige niet -periodieke hoeveelheid decimalen. Om deze reden is het moeilijk om de vierkantswortel van 3 handmatig te berekenen.

3 vierkante wortel

Als een rekenmachine wordt gebruikt, is te zien dat de vierkantswortel van 3 1.73205080756887 is ..

Nu zou je dit nummer handmatig kunnen proberen als volgt te benaderen:

-1*1 = 1 en 2*2 = 4, dit zegt dat de vierkantswortel van 3 een getal is tussen 1 en 2.

-1.7*1.7 = 2,89 en 1.8*1.8 = 3,24, daarom is het eerste decimale figuur 7.

-1.73*1.73 = 2,99 en 1.74*1.74 = 3,02, dus het tweede decimale figuur is 3.

-1.732*1.732 = 2,99 en 1.733*1.733 = 3.003, daarom is het derde decimale figuur 2.

En zo verder kunt u doorgaan. Dit is een handmatige manier om de vierkantswortel van 3 te berekenen.

Er zijn ook andere veel meer geavanceerde technieken, zoals de Newton-Raphson-methode, die een numerieke methode is om benaderingen te berekenen.

Waar kunnen we het nummer vinden √3?

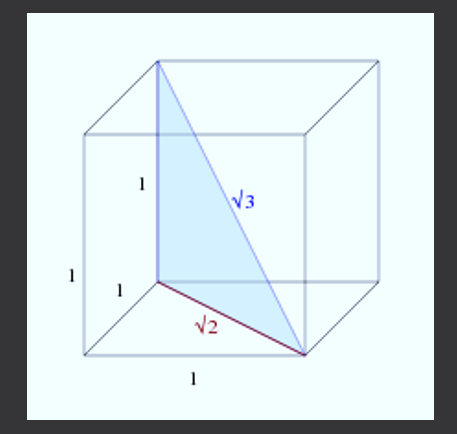
Vanwege het ingewikkelde nummer kan worden gedacht dat het niet in alledaagse objecten verschijnt, maar dit is onwaar. Als u een kubus (vierkante doos) heeft, zodat de lengte van de zijkanten 1 is, dan hebben de kubusdiagonalen een maat voor √3.

Om dit te verifiëren, wordt de Pythagoras -stelling gebruikt die zegt: Give.

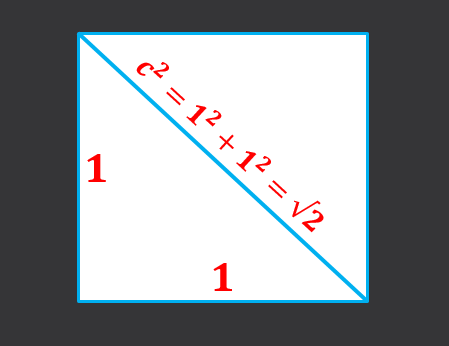
Met een zijde van zij 1, moet u diagonaal van het vierkant van de basis zijn, is gelijk aan de som van de vierkanten van de categorieën, dat wil zeggen C² = 1²+1² = 2, daarom de diagonaal van de basismaat √2.

Nu, om de kubusdiagonaal te berekenen, kunt u de volgende figuur zien.

De nieuwe rechthoekige driehoek heeft benen van lengtes 1 en √2, daarom wordt bij het gebruik van de stelling van Pythagoras om de lengte van zijn diagonaal te berekenen, verkregen: c² = 1²+(√2) ² = 1+2 = 3, het is zeg maar , C = √3.

Aldus is de lengte van de diagonaal van een zijemmer 1 gelijk aan √3.

√3 Een irrationeel nummer

In het begin werd gezegd dat √3 een irrationeel aantal is. Om dit te verifiëren, wordt aangenomen door de absurditeit die een rationeel getal is, dat er twee getallen "A" en "B" zijn, relatieve neven en nichten, zoals A/B = √3.

Wanneer de laatste gelijkheid en duidelijke "a²", wordt de volgende vergelijking verkregen: a² = 3*b². Dit zegt dat "a²" een veelvoud van 3 is, wat concludeert dat "a" een veelvoud van 3 is.

Omdat het "een" veelvoud van 3 is, is er een geheel getal "k" zodat a = 3*k. Daarom wordt het door het vervangen van de tweede vergelijking verkregen: (3*K) ² = 9*k² = 3*b², wat hetzelfde is als b² = 3*k².

Zoals voorheen leidt deze laatste gelijkheid tot de conclusie dat "B" een veelvoud van 3 is.

Concluderend, "A" en "B" zijn beide veelvouden van 3, wat een tegenstrijdigheid is, omdat in eerste instantie werd aangenomen dat ze relatieve neven en nichten waren.

Daarom is √3 een irrationeel aantal.