Wat zijn interne alternatieve hoeken? (Met oefeningen)

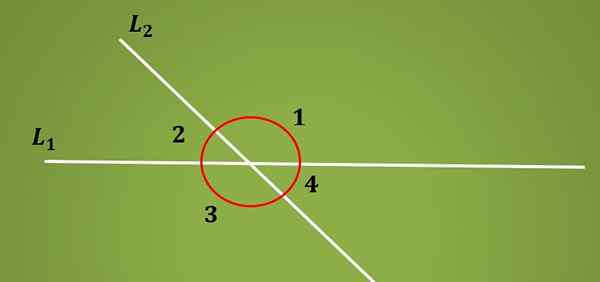
De interne alternatieve hoeken Het zijn die hoeken gevormd door de kruising van twee parallelle lijnen en een dwarse lijn. Wanneer een L1 -lijn wordt gesneden door een dwarse lijn worden L2 4 -hoeken gevormd.

De twee paren hoeken die aan dezelfde kant van de L1 -lijn blijven, worden aanvullende hoeken genoemd, omdat de som gelijk is aan 180º. In de onderste afbeelding zijn hoeken 1 en 2 aanvullend, evenals hoeken 3 en 4.

Om te praten over interne alternatieve hoeken, is het noodzakelijk om twee parallelle lijnen en een dwarse lijn te hebben; Zoals eerder te zien, zullen zich er acht hoeken vormen.

Wanneer er twee parallelle lijnen L1 en L2 zijn gesneden door een transversale lijn, worden acht hoeken gevormd, zoals geïllustreerd in de volgende afbeelding.

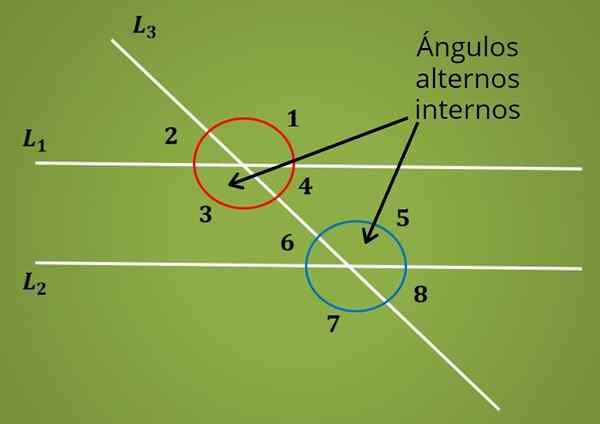
In het superieure beeld zijn de paren van hoeken 1 en 2, 3 en 4, 5 en 6, 7 en 8 aanvullende hoeken. 

Nu zijn de interne alternatieve hoeken die tussen de twee parallelle lijnen L1 en L2, maar bevinden zich aan de tegenovergestelde zijden van de transversale lijn L2. Dat is Hoeken 3 en 5 zijn intern alternatief. Evenzo zijn hoeken 4 en 6 interne alternatieve hoeken.

Tegenover de hoeken door het hoekpunt

Om het nut te kennen dat interne alternatieve hoeken hebben, is het eerst nodig om te weten dat als twee hoeken worden tegengewerkt door het hoekpunt, deze twee hoeken hetzelfde meten.

Bijvoorbeeld, hoeken 1 en 3 meet hetzelfde als ze worden tegengewerkt door het hoekpunt. Onder dezelfde redenering kan worden geconcludeerd dat hoeken 2 en 4, 5 en 7, 6 en 8 hetzelfde meten.

Hoeken gevormd tussen een secant en twee parallellen

Wanneer er twee parallelle lijnen zijn gesneden door een droge of transversale lijn zoals in de vorige figuur, is het waar dat hoeken 1 en 5, 2 en 6, 3 en 7, 4 en 8 hetzelfde meten.

Kan u van dienst zijn: Euler -nummer of nummer E: hoeveel OK, eigenschappen, applicaties

Interne alternatieve hoeken

Met behulp van de definitie van hoeken geplaatst door het hoekpunt en de eigenschap van de hoeken gevormd tussen een secant en twee parallelle lijnen, kan worden geconcludeerd dat de interne alternatieve hoeken dezelfde maatregel hebben.

Opgeloste oefeningen

- Eerste oefening

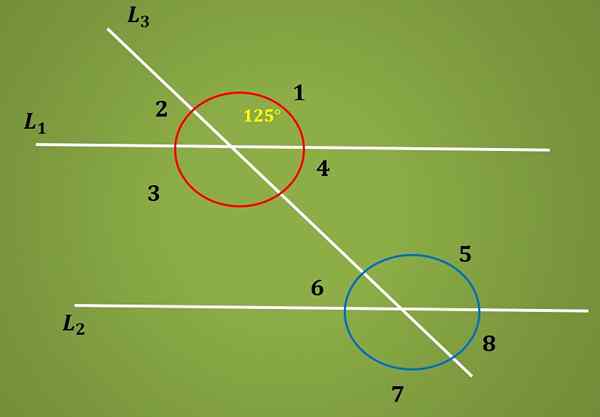
Bereken de maat van hoek 6 van de volgende afbeelding, wetende dat hoek 1 125º meet.

Oplossing

Aangezien hoeken 1 en 5 tegenover het hoekpunt zijn, heb je die hoek 3 meet 125º. Nu, omdat hoeken 3 en 5 intern alternatief zijn, heb je dat hoek 5 ook 125º meet.

Ten slotte, aangezien hoeken 5 en 6 aanvullend zijn, is de maat voor hoek 6 noodzakelijk gelijk aan 180º - 125º = 55º.

- Tweede oefening

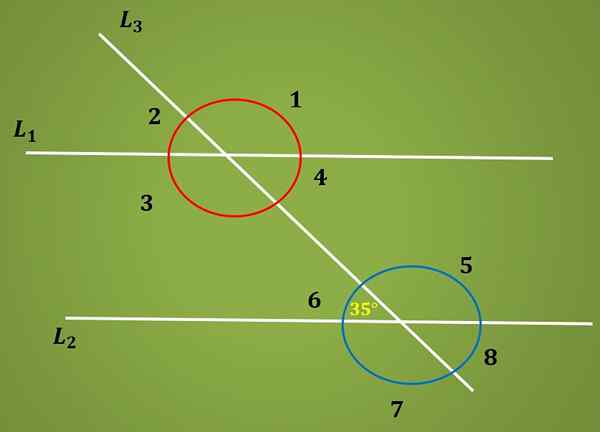
Bereken de hoek 3 wetende dat hoek 6 35º meet.

Oplossing

Het is bekend dat hoek 6 35º meet, en het is ook bekend dat hoeken 6 en 4 intern alternatief zijn, daarom meten ze hetzelfde. Dat wil zeggen dat Angle 4 35º meet.

Aan de andere kant, met behulp van het feit dat hoeken 4 en 3 aanvullend zijn, is de maat voor hoek 3 gelijk aan 180º - 35º = 145º.

Observatie

Het is noodzakelijk dat de lijnen parallel zijn zodat ze de overeenkomstige eigenschappen kunnen ontmoeten.

De oefeningen kunnen sneller worden opgelost, maar dit artikel wilde de eigenschap van interne alternatieve hoeken gebruiken.

Referenties

1. Bourke. (2007). Een invalshoek over geometrie wiskundewerkboek. NewPath Learning.
2. Clemens, s. R., O'Dafer, p. G., & Cooney, t. J. (1998). Geometrie. Pearson Education.
3. Lang, s., & Murrow, g. (1988). Geometrie: een middelbare schoolcursus. Springer Science & Business Media.
4. Lira, a., Jaime, p., Chavez, m., Gallegos, m., & Rodríguez, c. (2006). Geometrie en trigonometrie. Umbrale edities.
5. Moyano, een. R., Saro, een. R., & Ruiz, r. M. (2007). Algebra en kwadratische geometrie. Netbiblo.
6. Sullivan, m. (1997). Trigonometrie en analytische geometrie. Pearson Education.
7. Wingard-Enelson, r. (2012). Geometrie. Enslow Publishers, Inc.

Kan u van dienst zijn: impliciete derivaten: hoe ze worden opgelost en opgeloste oefeningen