Wat is een deterministisch experiment?

Hij deterministisch experiment, In statistieken is het een die een voorspelbaar en reproduceerbaar resultaat heeft, zolang dezelfde beginvoorwaarden en parameters worden gehandhaafd. Dat wil zeggen, de oorzaak-gevolg relatie is in zijn geheel bekend.

De tijd die het zand van de ene klok neemt om van het ene compartiment naar het andere te gaan, is een deterministisch experiment, omdat het resultaat voorspelbaar en reproduceerbaar is. Zolang de omstandigheden hetzelfde zijn, duurt het dezelfde tijd om van capsule naar capsule te gaan.

Figuur 1. De tijd die het zand van het ene compartiment naar het andere brengt, is een deterministisch experiment. Bron: Pixabay

Veel fysieke fenomenen zijn deterministisch, sommige voorbeelden zijn de volgende:

- Een dichtste object dan water, zoals een steen, zal altijd zinken.

- Een vlotter, die minder dicht is dan het water, zal altijd drijven (tenzij er een kracht wordt ondergedompeld) wordt uitgeoefend).

- De kooktemperatuur van water op zeeniveau is altijd 100 ºC.

- De tijd die nodig is om een ​​gegeven te vallen die daalt van rust, omdat het wordt bepaald door de hoogte waaruit het is gedropt en deze keer altijd hetzelfde is (wanneer het op dezelfde hoogte wordt vrijgegeven).

Profiteren van het voorbeeld van de dobbelstenen. Als dit wordt gevallen, zelfs als u voorzichtig bent om dezelfde oriëntatie te geven en altijd op dezelfde hoogte is, is het moeilijk om te voorspellen welk gezicht het zal verschijnen zodra het op de grond is gestopt. Dit zou een willekeurig experiment zijn.

Theoretisch, als ze bekend waren met oneindige precisiegegevens zoals: positie; initiële snelheid en dobbelstenen oriëntatie; vorm (afgeronde of hoekige randen); en de restitutiecoëfficiënt van het oppervlak waarop het valt, misschien zou het mogelijk zijn om te voorspellen, door middel van complexe berekeningen, welk gezicht de dobbelstenen zal laten zien wanneer het stopt. Maar elke kleine variatie in de startomstandigheden zou een ander resultaat opleveren. 

Dergelijke systemen zijn deterministisch en tegelijkertijd chaotisch, omdat een kleine wijziging van de beginvoorwaarden het eindresultaat op een willekeurige manier verandert.

Kan u van dienst zijn: Systeem van vergelijkingen: oplossingsmethoden, voorbeelden, oefeningen

[TOC]

Meting

De deterministische experimenten zijn volledig meetbaar, maar toch is de meting van hun resultaat niet oneindig nauwkeurig en heeft een bepaalde marge van onzekerheid.

Laten we bijvoorbeeld het volgende experiment, volledig deterministisch plaatsen: een speelgoedauto loslaat op een rechte helling.

Figuur 2. Een auto daalt af door een rechtlijnige helling in een deterministisch experiment. Bron: Pixabay.

Het wordt altijd vrijgelaten vanuit hetzelfde startpunt, en zorg ervoor dat u geen impuls geeft. In dit geval moet de tijd die de auto nodig heeft om de baan te reizen altijd hetzelfde zijn.

Nu is een kind van plan om de tijd die hij naar de winkelwagen neemt, te meten. Hiervoor gebruikt u de stopwatch die is opgenomen in uw mobiele telefoon.

Als waarnemer jongen, het eerste dat je opmerkt, is dat je meetinstrument een eindige precisie heeft, omdat het minste tijdsverschil dat de stopwatch kan meten 1 honderdste van de tweede is.

Dan gaat het kind verder met het uitvoeren van het experiment en met de mobiele stopwatch meet 11 keer - laten we zeggen dat zeker de tijd die hij naar de kinderwagen ging om het hellende vlak te reizen, waarbij de volgende resultaten werden verkregen:

3.12S 3.09S 3,04S 3.04S 3.10S 3.08S 3.05S 3.10s 3.11s 3,06s en 3,03s.

Het kind is verrast, want op school hadden ze hem verteld dat dit een deterministisch experiment is, maar in elke mate verkreeg hij een iets ander resultaat.

Variaties voor zover

Wat kunnen de oorzaken zijn die in elke meting een ander resultaat hebben? 

Een oorzaak kan de nauwkeurigheid van het instrument zijn, dat is 0,01's zoals het al is gezegd. Maar merk op dat de verschillen in de metingen boven die waarde liggen, dus moet worden gedacht aan andere oorzaken, zoals:

- Kleine variaties van het startpunt.

- Verschillen aan het begin en stop van de stopwatch, vanwege de reactietijd van het kind.

Wat betreft de reactietijd, treedt een vertraging zeker op, omdat het kind ziet dat de kar begint te bewegen, totdat de stopwatch aandringt. 

Kan u van dienst zijn: randen van een kubus

Evenzo is er bij aankomst een vertraging vanwege de tijd tot reactie. Maar start- en aankomstvertragingen worden gecompenseerd, zodat de verkregen tijd heel dicht bij het echte moet zijn. 

In elk geval is de compensatie voor reactievertraging niet exact, omdat reactietijden kleine variaties kunnen hebben in elke proef, wat de verschillen in de resultaten verklaart.

Wat is dan het ware resultaat van het experiment?

Resultaten van een meet en fout

Om het eindresultaat te melden, moeten we statistieken gebruiken. Laten we eerst kijken hoe vaak de resultaten worden herhaald:

- 3.03S (1 keer)

- 3.04s (2 keer)

- 3.05S (1 keer)

- 3.06S (1 keer)

- 3.08S (1 keer)

- 3.09S 1 keer

- 3.10s (2 keer)

- 3.11s (1 keer)

- 3.12s (1 keer)

Bij het bestellen van de gegevens realiseren we ons dat een mode of meer herhaald resultaat. Dan is het resultaat om te rapporteren het rekenkundig gemiddelde, dat als volgt kan worden berekend:

) 1 + 2 + 1 + 1).

Het resultaat van de vorige berekening is 3.074545455. Logischerwijs heeft het geen zin om al deze decimalen in het resultaat te melden, omdat elke meting niets heeft plus 2 precisie -decimalen. 

Door de afrondregels toe te passen, kan worden gezegd dat de tijd die nodig is voor de CART -tour, de baan het afgeronde rekenkundige gemiddelde is voor twee decimale cijfers.

Het resultaat dat we kunnen melden voor ons experiment is:

3.08 seconden is de tijd die u naar de speelgoedauto gaat, reist het hellende track.

- Meetfout

Zoals te zien in ons voorbeeld van een deterministisch experiment, heeft elke meting een fout, omdat deze niet kan worden gemeten met oneindige precisie.

In elk geval is het enige dat kan worden gedaan om instrumenten en meetmethoden te verbeteren om een ​​preciezer resultaat te verkrijgen.

In de vorige sectie gaven we een resultaat voor ons deterministische experiment van de tijd die naar de speelgoedauto nodig is om een ​​hellend spoor te reizen. Maar dit resultaat impliceert een fout. Nu zullen we uitleggen hoe we die fout kunnen berekenen.

Het kan u van dienst zijn: rechthoekige coördinaten: voorbeelden en oefeningen opgelost

- Berekening van de meetfout

In de metingen voor tijd is er een dispersie in de gemaakte maatregelen. De standaardafwijking Het is een vaak gebruikte statistische vorm om gegevensdispersie te melden. 

Variantie en standaardafwijking

De manier om de standaardafwijking te berekenen is als volgt: eerst is de variantie van de gegevens, op deze manier gedefinieerd:

De som van de verschillen van elk resultaat met het rekenkundige gemiddelde, kwadraat en gedeeld door het totale aantal gegevens

Als de vierkantswortel naar de variantie wordt gebracht, wordt de standaardafwijking verkregen.

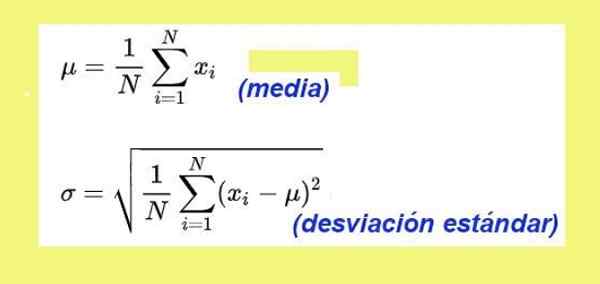figuur 3. Gemiddelde formules en standaardafwijking. Bron: Wikimedia Commons.

De standaardafwijking voor de daaltijdgegevens van de speelgoed Auton is:

σ = 0,03

Het resultaat werd afgerond op 2 decimalen, omdat de precisie van elk van de gegevens 2 decimalen is. In dit geval vertegenwoordigt 0,03S de statistische fout van elk van de gegevens.

Het gemiddelde rekenkundige gemiddelde van de verkregen tijden heeft echter een lagere fout. De gemiddelde fout wordt berekend door de standaardafwijking tussen de vierkantswortel van het totale gegevensnummer te delen.

Gemiddelde fout = σ / √n = 0,03 / √11 = 0,01

Dat wil zeggen, de statistische fout van de gemiddelde tijd is 1honderdste seconde en in dit voorbeeld valt het samen met de waardering van de stopwatch, maar het is niet altijd zo.

Als eindresultaat van de maatregel wordt dan gerapporteerd:

 T = 3,08s ± 0,01s is de tijd die het kost naar de speelgoedauto om het hellende spoor te reizen.

Er wordt geconcludeerd dat zelfs als het gaat om een ​​deterministisch experiment, het resultaat van de meting ervan geen oneindige precisie heeft en altijd een foutmarge heeft. 

En bovendien, om het eindresultaat te melden, is het noodzakelijk, zelfs als het gaat om een ​​deterministisch experiment, gebruik dan statistische methoden.

Referenties

1. Canalphi. Deterministisch experiment. Hersteld van: YouTube.com
2. Mathemovil. Deterministisch experiment. Hersteld van: YouTube.com
3. Pishro Nick H . Inleiding tot waarschijnlijkheid. Opgehaald uit: waarschijnlijkheid Course.com
4. Ross. Waarschijnlijkheid en statistieken voor ingenieurs. MC-GRAW HILL.
5. Statistieken hoe. Deterministisch: definitie en examens. Hersteld van: StatisticShowto.Datascienceceral.com
6. Wikipedia. Typische afwijking. Hersteld van: is.Wikipedia.com
7. Wikipedia. Experiment (waarschijnlijkheidstheorie). Opgehaald uit: in.Wikipedia.com