Wat is lineaire snelheid? (Met opgeloste oefeningen)

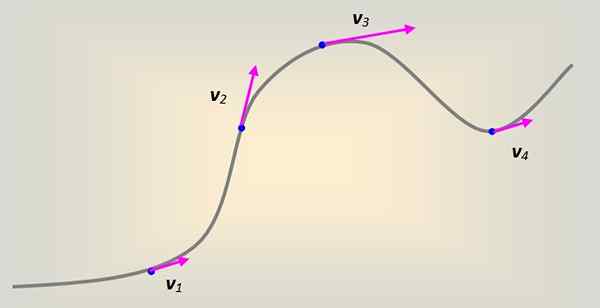
De Lineaire snelheid Het wordt gedefinieerd als dat wat altijd tangentieel is voor het traject gevolgd door het deeltje, ongeacht. Als het deeltje altijd beweegt in een rechtlijnig traject, is er geen probleem om me voor te stellen hoe de snelheidsvector deze rechte lijn vergezelt.

Over het algemeen wordt de beweging echter willekeurig op een curve uitgevoerd. Elk deel van de curve kan worden gemodelleerd alsof het deel uitmaakt van een radiocirkel naar, die op elk punt is geraakt aan het gevolgde pad.

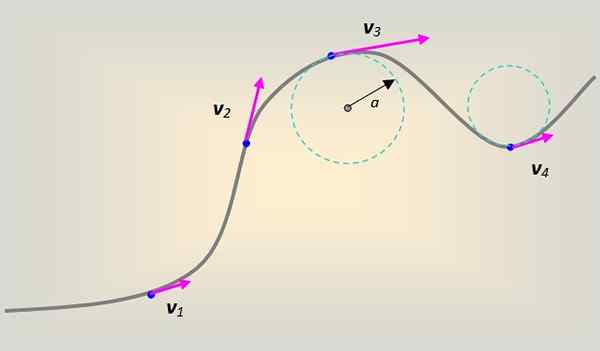Figuur 1. Lineaire snelheid op een mobiel die een kromlijnig traject beschrijft. Bron: zelf gemaakt.

In dit geval gaat de lineaire snelheid tangentieel en te allen tijde op de curve op elk punt ervan.

Wiskundig onmiddellijke lineaire snelheid is de afgeleide van de positie ten opzichte van de tijd. Zijn R de positievector van het deeltje in een oogwenk T, Dan wordt de lineaire snelheid gegeven door de uitdrukking:

v = R'(T) = DR / DT

Dit betekent dat lineaire snelheid of tangentiële snelheid, zoals het ook wordt genoemd, niets anders is dan de verandering van de positie ten opzichte van de tijd.

[TOC]

Lineaire snelheid in cirkelvormige beweging

Wanneer de beweging op een omtrek is, kunnen we op elk punt naast het deeltje gaan en zien wat er gebeurt in twee zeer speciale richtingen: een daarvan is degene die altijd naar het midden wijst. Dit is het adres radiaal.

De andere belangrijke richting is degene die plaatsvindt op de omtrek, dit is het adres tangentieel En de lineaire snelheid heeft het altijd.

Kan u van dienst zijn: Manometrische druk: uitleg, formules, vergelijkingen, voorbeelden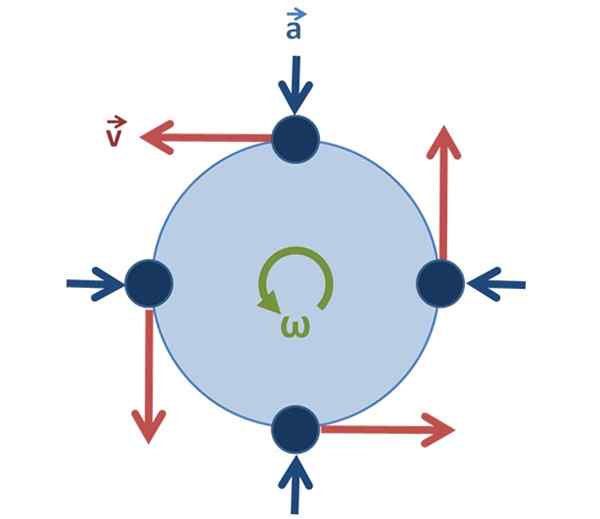Figuur 2. Uniforme cirkelvormige beweging: de snelheidsvector verandert van richting en richting terwijl het deeltje roteert, maar de grootte ervan is hetzelfde. Bron: Original by User: Brews_ohare, SVVED BY User: Sjlegeg [CC BY-SA 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)].

In het geval van de uniforme cirkelvormige beweging is het belangrijk ja, het blijft ongewijzigd.

Voor deze beweging wordt de positie als functie van tijd gegeven door S (t), waar S is hij Tourd Arc En T Het is de tijd. In dat geval wordt de onmiddellijke snelheid gegeven door de uitdrukking V = ds/dt En het is constant.

Als de grootte van de snelheid ook varieert (we weten al dat de richting het altijd doet, anders kan de mobiel niet draaien), worden we geconfronteerd met een gevarieerde cirkelvormige beweging, waarbij mobiel naast roteren kan stoppen of versnellen.

Lineaire snelheid, hoeksnelheid en centripetale versnelling

De deeltjesbeweging kan ook worden gezien vanuit het oogpunt van de vegende hoek, In plaats van het te doen van het gereisde doel. In dit geval is er sprake van de hoekige snelheid. Voor een beweging op een radiocirkel R, Er is een relatie tussen de boog (in radialen) en de hoek:

S = r θ

Afleiden met betrekking tot beide partijen:

ds/dt = r (dθ/dt)

Het derivaat van θ aanroepen met betrekking tot T als hoekige snelheid En het aangeven met de Griekse letter ω "Omega", je hebt deze relatie:

v = ωR

Centripetale versnelling

Elke cirkelvormige beweging heeft centripetale versnelling, dat is altijd gericht op het midden van de omtrek. Ze zorgt ervoor dat de snelheid verandert om met het deeltje te bewegen terwijl het draait.

Het kan u van dienst zijn: Kalibratiecurve: waar is het voor, hoe het te doen, voorbeelden

Centripetale versnelling naar_C of naar_R Het wijst altijd naar het midden (zie figuur 2) en is op deze manier gerelateerd aan de lineaire snelheid:

naar_C = V² /R

En met hoeksnelheid als:

naar_C = (ΩR)² /R = ω²R

Voor een uniforme cirkelvormige beweging, de positie S (t) Het is van de vorm:

S (t) = So+ vt

Bovendien moet de gevarieerde cirkelvormige beweging een component van de versnelling hebben die wordt genoemd Tangentiële versnelling naar_T, Dat gaat over het veranderen van de omvang van de lineaire snelheid. Ja naar_T  het is constant, De positie is:

S (t) = s_of + v_ofT + ½ a_TT²

Met v_of Zoals de initiële snelheid.

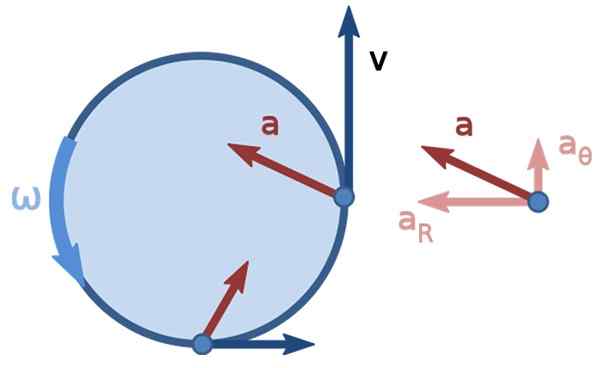figuur 3. Niet -uniforme cirkelvormige beweging. Bron: nonuniform_circular_motion.PNG: Brews Oharedorivative Work: Kooning Jons [CC BY-SA 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)].

Opgeloste lineaire snelheidsoefeningen

De opgeloste oefeningen dragen bij om het juiste gebruik van de gegeven concepten en vergelijkingen te verduidelijken.

-Oefening opgelost 1 

Een insect beweegt op een radius halve cirkel r = 2 m, beginnend bij rust op punt een terwijl hij zijn lineaire snelheid verhoogt, met een snelheid van p m/s². Zoek: a) Na hoe laat bereikt het punt B, b) de lineaire snelheidsvector op dat moment, c) de vectorversnelling op dat moment op dat moment.

Figuur 4. Een insect begint vanaf A en bereikt B op een halfronde traject. Het heeft een lineaire snelheid. Bron: zelf gemaakt.

Oplossing

a) De verklaring geeft aan dat tangentiële versnelling constant is en π m/s waard is², Dan is het geldig om de vergelijking te gebruiken voor uniform gevarieerde beweging:

S (t) = s_of + v_ofT + ½ a_T.T²

Met s_of = 0 en V_of = 0:

S (t) = ½ a_T.T²

S = πR (De helft van de omtreklengte)

T = (2. πR /naar_T)) ^½ S = (2π.2 /π))^½S = 2 S

B) v (t) = v_of + naar_T. T = 2π Mevr

Wanneer op punt B wijst de lineaire snelheidsvector in de verticale richting naar beneden in de richting (-En):

Kan u van dienst zijn: wat is de diëlektrische constante?

v (t) = 2π Mevr((-En))

c) Tangentiële versnelling is al gehouden, centripetale versnelling ontbreekt om de snelheidsvector te hebben naar:

naar_C = V² / R = (2π))² / 2 m/ s² = 2π² Mevr²

naar = a_C ((-X) + a_T ((-En) = 2π²((-X)+ π ((-En) Mevr²

-Oefening opgelost 2

Een deeltje draait in een radiocirkel 2.90 m. Op een bepaald moment is de versnelling de waard 1.05 m/s² in een richting die 32 vormt met zijn bewegingsrichting. Vind je lineaire snelheid op: a) dit moment, b) 2 seconden later, ervan uitgaande dat tangentiële versnelling constant is.

Oplossing

a) Het directoraat voor bewegingen is precies het tangentiële adres:

naar_T = 1.05 m/s² . cos 32º = 0.89 m/s² ; naar_C = 1.05 m/s² . Sen 32º = 0.56 m/s²

De snelheid verdwijnt naar_C = V² / R als:

v = (r.naar_C))^1/2  = 1.27 m/s

b) De vergelijking voor uniform gevarieerde beweging is als volgt geldig: v = v_of + naar_TT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill. 84-88.
2. Figueroa, D. Fysieke serie voor wetenschap en engineering. Deel 3. Editie. Kinematica. 199-232.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6^e… Ed Prentice Hall. 62-64.
4. Relatieve beweging. Hersteld van: cursussen.Lumenarning.com
5. Wilson, J. 2011. Natuurkunde 10. Pearson Education. 166-168.