Wat is capacitieve reactantie en hoe deze te berekenen?

De capacitieve reactantie Het is de weerstand dat een condensor, een regulerend element van de belastingsstroom in een wisselstroomcircuit, tegen de doorgang van de stroom is.

In een circuit uit een condensor en geactiveerd door een wisselstroombron, kan capacitieve reactantie X worden gedefinieerd_C als volgt:

X_C = 1 / ωc

Figuur 1. Capacitieve reacties maken deel uit van Passabajos -filters en sprekers van sprekers. Bron: Pixabay.

Of ook:

X_C = 1 / 2πfc

Waarbij C de capaciteit van de condensator is en ω de hoekfrequentie van de bron is, gerelateerd aan de frequentie F tot:

Ω = 2πf

De capacitieve reactantie hangt af van de inverse van de frequentie, daarom is bij hoge frequenties meestal klein, terwijl bij lage frequenties de reactantie groot is.

De internationale systeemeenheid om de capacitieve reactantie te meten is de OHM (ω), op voorwaarde dat de capaciteit van de condensator in Farad is, (afgekort F) en de frequentie wordt uitgedrukt in het omgekeerde van seconden (s^-1)).

Terwijl de belasting duurt, worden een spanning en een stroom ook vastgesteld via de condensator, waarvan de maximale amplitudes of waarden respectievelijk worden aangeduid als V_C en ik_C, Ze zijn gerelateerd door capacitieve reactantie analoog aan de wet van Ohm:

V_C = I_C ⋅ x_C

In een condensor wordt de spanning 90º vertraagd ten opzichte van de stroom, of deze is 90º gevorderd ten opzichte van dat, zoals voorkeur. In elk geval is de frequentie hetzelfde.

Wanneer x_C Het is erg groot, de stroom is meestal klein en maakt de waarde van x oneindig_C, De condensor gedraagt ​​zich als een open circuit en de stroom is nul.

[TOC]

Hoe capacitieve reactantie te berekenen

Laten we eens kijken naar een voorbeeld van het berekenen van de capacitieve reactantie: Stel dat een 6 μF -condensator is verbonden met een afwisselend stroomuitgang en frequentie en frequentie F 60 Hz.

Om de capacitieve reactantie te vinden, wordt de definitie van het begin gebruikt. De hoekfrequentie ω wordt gegeven door:

Het kan u van dienst zijn: magnetische inductie: formules, hoe het wordt berekend en voorbeelden

Ω = 2πf = 2π x 60 Hz = 377 s^-1

Dan wordt dit resultaat vervangen in de definitie:

X_C = 1 / ωc = 1 / (377 s^-1x 6 x10 ^-6 F) = 442.1 ohm

Laten we nu eens kijken naar de amplitude van de stroom die in het circuit circuleert. Omdat de bron een amplitude -spanning V biedt_C = 40 V, we gebruiken de relatie tussen capacitieve reactantie, stroom en spanning om de amplitude van de maximale stroom of stroom te berekenen:

Je_C = V_C / X_C = 40 V / 442.1 ohm = 0.09047 A = 90.5 m a.

Als de frequentie erg groot wordt, wordt de capacitieve reactantie klein, maar als de frequentie 0 werd en we een directe stroom hadden, zou de reactantie de neiging hebben oneindig te zijn.

Stroom- en condensorspanning

Wanneer een condensor verbinding maakt met een wisselstroombron, zoals deze oscilleert en zijn polariteit verandert, ervaart de condensator ladingen en ontladingen afwisselend ontlading.

Voor een frequentie van 60 Hz zoals het voorbeeld, is de spanning 60 keer per seconde positief en negatief nog 60 keer per seconde.

Figuur 2. Eenvoudig condensorcircuit en een wisselstroombron. Bron: f. Zapata.

Door de spanning te vergroten, drijft het de stroom in één richting, maar als de condensor downloadt, komt er stroom in de tegenovergestelde richting.

Ja V_C (t) = V_M Sen ωt, wetende dat de capaciteit de reden is tussen de belasting en de spanning, hebben we de belasting:

C = q/v → q (t) = cv = cv_M Sen ωt

En met de lading afhankelijk van tijd, hebben we de stroom, wat de afgeleide daarvan is:

Je_C(t) = cv_M Ω cos ωt

Maar borst en cosinus zijn gerelateerd door: cos α = sin (α + π/2), daarom:

Je_C(t) = cv_M Ω sen (ωt + π/2) = i_C Sen (ωt + π/2)

Met i_C = CV_C Ω

Zoals te zien is, is er een verschil van 90º vooruitgang van de stroom ten opzichte van de spanning, zoals in het begin becommentarieerd.

Kan u van dienst zijn: Millikan Experiment: procedure, uitleg, belang

In de beschrijving van dit type circuits, het concept van Fasor, die veel op een vector lijkt en in het complexe vlak elke afwisselende hoeveelheid zoals stroom, spanning of impedantie kan vertegenwoordigen.

De volgende figuur toont rechts de spanning en stroomfasores in de condensator, die een hoek van 90º vormen, wat de vertraging is tussen de twee.

Links zijn de respectieve grafieken, van verschillende amplitudes, maar gelijke frequentie. Na verloop van tijd is de huidige vooruitgang naar de spanning en wanneer dit maximaal is, is de stroom nul en wanneer de spanning nul is, is de stroom maximaal maar met de omgekeerde polariteit.

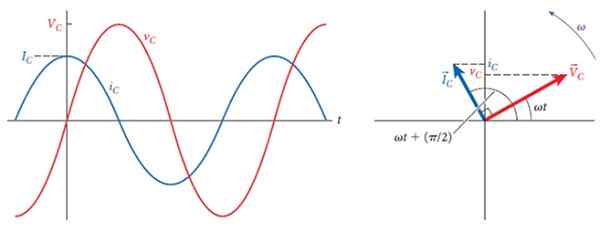figuur 3. 90º vertraging tussen de stroom en de spanning door een condensator. Bron: Bauer, W.

Complexe condensorimpedantie

In een circuit met weerstanden, condensatoren en inductanties is reactantie het denkbeeldige deel van de z -impedantie, een complexe hoeveelheid die in wisselstroomcircuits een rol heeft die vergelijkbaar is met die van elektrische weerstand voor directe stroom die van directe stroom.

In feite wordt de impedantie van een circuit gedefinieerd als de reden tussen de spanning en de stroom:

Z = v / i

Voor een condensator of condensator wordt de impedantie ervan gegeven door het quotiënt:

Z_C = v (t) / i (t) = v_C Sen ωt / i_C Sen (ωt + π/2)

Een manier om spanning en stroom als fasores tot uitdrukking te brengen, is door de amplitude en fasehoek (polaire vorm) aan te geven:

v (t) = v_C ∠ 0º

I (t) = i_C ∠ 90º

Daarom:

Z_C = V_C ∠ 0º / i_C ∠ 90º = (V_C / Yo_C) ∠ 0º -90º =

= V_C / CV_C Ω ∠ -90º = (1/ ωc) ∠ -90º =

Z_C = (- j) x_C

Dat wil zeggen, de impedantie van de condensor is de capacitieve reactantie vermenigvuldigd met het negatieve van de denkbeeldige eenheid.

Impedantie van een serie RC -circuit

De impedantie van een wisselstroomcircuit met weerstand, condensatoren en inductoren kan ook binomiaal worden weergegeven door:

Het kan u van dienst zijn: eerste wet van thermodynamica: formules, vergelijkingen, voorbeelden

Z = r + jx

In deze vergelijking vertegenwoordigt r de weerstand, die overeenkomt met het echte deel, J is de denkbeeldige eenheid en X is de reactantie, die capacitief of inductief kan zijn of van beide, als deze elementen tegelijkertijd in het circuit aanwezig zijn.

Als het circuit een weerstand en een seriële condensator bevat, is de impedantie ervan:

Z = z_R + Z_C    

Zoals in weerstandsspanning en stroom zijn in fase, is resistieve impedantie gewoon de waarde van weerstand R.

In het geval van capacitieve impedantie hebben we al gezien dat Z_C = -JX_C , Daarom is de impedantie van het RC -circuit:

Z = r - jx_C = R - j (1/ ωc)

Bijvoorbeeld in het onderstaande circuit, waarvan de bron van de vorm is:

100 V ⋅ sen (120πt)

Opmerking dat ω = 120π, de impedantie is:

Z = 83.0 - j [(1 / (120π ⋅ 6 x 10^-6)] ohm = 83.0 - 442.1 J ohm.

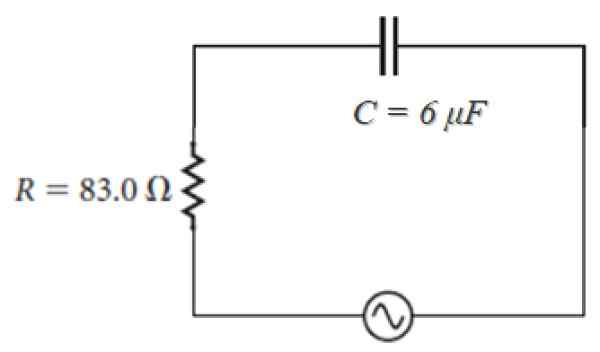Figuur 4. RC Circuit -serie met wisselstroombron. Bron: f. Zapata.

Capacitieve reactantietoepassingen

PASA Hoge filters, lage passfilters, brugcircuits om capaciteiten en inductanties en koelkastcircuits te meten, behoren.

In geluidsapparatuur worden sommige luidsprekers geleverd met afzonderlijke soorten type Woofer (groter) voor lage frequenties en Tweeter of kleine hoorn voor hoge frequenties. Op deze manier verbetert de prestaties en kwaliteit van audio.

Ze zijn condensatoren gebruikt die de aankomst van lage frequenties in de tweeter voorkomen, terwijl een inductor wordt toegevoegd in de woofer om hoge frequentiesignalen te voorkomen, omdat inductantie een reactantie heeft die evenredig is aan de frequentie: x x_L = 2πfl.

Referenties

1. Alexander, c. 2006. Elektrische circuitfunderingen. 3e. Editie. MC Graw Hill.
2. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 2. MC Graw Hill.
3. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 6. Elektromagnetisme. Uitgegeven door Douglas Figueroa (USB).
4. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
5. Serway, r., Jewett, J. 2008. Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.