Wat is akoestische impedantie? Toepassingen en oefeningen

De akoestische impedantie o Specifieke akoestische impedantie is de weerstand van materiële middelen tegen de doorgang van geluidsgolven. Het is constant voor een bepaald medium, dat van een rotsachtige laag in de aarde naar het biologische weefsel gaat.

Duiden als Z akoestische impedantie, op wiskundige manier moet het:

Z = ρ.v

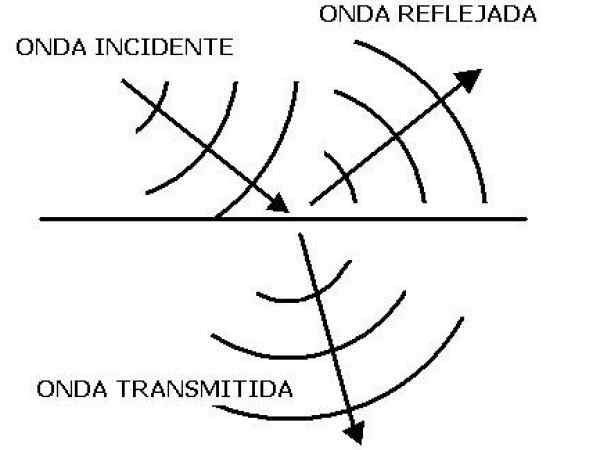
Figuur 1. Wanneer een geluidsgolf de rand van twee verschillende middelen beïnvloedt, wordt het ene deel gereflecteerd en wordt een ander overgedragen. Bron: Wikimedia Commons. Cristobal aeorum/cc by-sa (https: // creativeCommons.Org/licenties/by-sa/4.0)

Waarbij ρ dichtheid is en v de snelheid van het geluid van het medium. Deze uitdrukking is geldig voor een vlakke golf door in een vloeistof te bewegen.

In eenheden van het internationale systeem komt de dichtheid in kg/m³ en de snelheid in m/s. Daarom zijn de eenheden van akoestische impedantie kg/m².S.

Evenzo wordt akoestische impedantie gedefinieerd als het quotiënt tussen druk P en snelheid:

Z = p/v

Op deze manier uitgedrukt, is Z analoog aan elektrische weerstand r = v/i, waarbij de druk het spanningspapier vertegenwoordigt en dat van de stroom versnelt. Andere Z -eenheden als ze PA zouden zijn.s /m o n.GIJ³, volledig gelijkwaardig aan die eerder gegeven.

[TOC]

Transmissie en reflectie van de geluidsgolf

Als je twee verschillende middelen van impedanties hebt z₁ en z₂, Een deel van een geluidsgolf die de interface van beide beïnvloedt, kan worden overgedragen en een ander onderdeel kan worden gereflecteerd. Deze gereflecteerde of echo -golf is degene die belangrijke informatie bevat over het tweede medium.

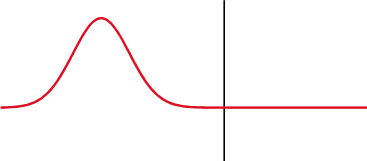Figuur 2. Invallende puls, verzonden puls en puls gereflecteerd. Bron: Wikimedia Commons.

De manier waarop de door de golf getransporteerde energie wordt verdeeld, hangt af van de reflectiecoëfficiënten R- en T -transmissie, twee zeer nuttige hoeveelheden om de verspreiding van de geluidsgolf te bestuderen. Want de reflectiecoëfficiënt is het quotiënt:

R = i_R /Yo_of

Waar ik_of Het is de intensiteit van de invallende golf_R Het is de intensiteit van de gereflecteerde golf. Evenzo heb je de transmissiecoëfficiënt:

T = i_T / Yo_of

Nu kan worden aangetoond dat de intensiteit van een vlakke golf evenredig is met de breedte van:

Het kan u van dienst zijn: Durometer: waar is het voor, hoe werkt, onderdelen, typen

I = (1/2) z.Ω² .NAAR²

Waarbij z de akoestische impedantie van het medium is en ω de frequentie van de golf is. Aan de andere kant is de verhouding tussen de overgedragen amplitude en de invallende amplitude:

NAAR_T/NAAR_of = 2z₁/(Z₁ +Z₂))

Die het quotiënt toestaat en_T /Yo_of  Het wordt uitgedrukt in termen van de amplitudes van de invallende golven en verzonden als:

Je_T /Yo_of = Z₂NAAR_T² / Z₁NAAR_of²

Door deze uitdrukkingen worden r en t verkregen in termen van akoestische impedantie z.

Transmissie- en reflectiecoëfficiënten

Het voorste quotiënt is precies de transmissiecoëfficiënt:

T = (z₂/Z₁) [2.Z₁/(Z₁ +Z₂)]² = 4Z₁Z₂ /(Z₁ +Z₂))²

Aangezien verliezen niet worden overwogen, is het vervuld dat de incidentintensiteit de som is van de overgedragen intensiteit en de gereflecteerde intensiteit:

Je_of = I_R + Je_T → (i_R / Yo_of) + (I_T / Yo_of) = 1

Dit stelt ons in staat om een ​​uitdrukking te vinden voor de reflectiecoëfficiënt in termen van de impedanties van de twee media:

R + t = 1 → r = 1 - t

Door wat algebra uit te voeren om de termen te herschikken, is de reflectiecoëfficiënt:

R = 1 - 4Z₁Z₂ /(Z₁ +Z₂))² = (Z₁ - Z₂))²/(Z₁ +Z₂))²

En zoals in de gereflecteerde puls is de informatie met betrekking tot het tweede medium, de reflectiecoëfficiënt is van groot belang.

Dus wanneer de twee media een groot verschil in impedantie hebben, wordt de teller van de vorige uitdrukking groter. Dan is de intensiteit van de gereflecteerde golf hoog en bevat ze goede informatie over het medium.

Wat betreft het deel van de golf die naar dat tweede medium wordt overgedragen, het wordt geleidelijk verzwakt en wordt de energie afgevoerd als warmte.

Toepassingen en oefeningen

Transmissie- en reflectiefenomenen geven aanleiding tot verschillende zeer belangrijke toepassingen, bijvoorbeeld de sonar die tijdens de Tweede Wereldoorlog is ontwikkeld en die dient om objecten te detecteren. Trouwens, sommige zoogdieren zoals vleermuizen en dolfijnen hebben een ingebouwd sonarsysteem.

Deze eigenschappen worden ook op grote schaal gebruikt om het interieur van de aarde te bestuderen in de seismische prospectiemethoden, bij het verkrijgen van medische beelden door echografie, de meting van botdichtheid en het vastleggen van beelden van verschillende structuren op zoek naar mislukkingen en defecten.

Kan u van dienst zijn: Thomson Atomic Model: kenmerken, postulaten, subatomaire deeltjes

Akoestische impedantie is ook een belangrijke parameter bij het evalueren van de geluidsreactie van een muziekinstrument.

- Oefening opgelost 1

De echografie -techniek om biologische weefselbeelden te verkrijgen maakt gebruik van hoogfrequente geluidspulsen. Echo's bevatten informatie over de organen en weefsels die doorgaan, dat software verantwoordelijk is voor het vertalen in een afbeelding.

Een echografie wordt beïnvloed door de vetmusculusinterface. Zoek met de verstrekte gegevens:

a) de akoestische impedantie van elke stof.

b) Het percentage echografie weerspiegeld in het grensvlak tussen vet en spieren.

Vet

• Dichtheid: 952 kg/m³
• Geluidssnelheid: 1450 m/s

Spier

• Dichtheid: 1075 kg/m³
• Geluidssnelheid: 1590 m/s

Oplossing voor

De akoestische impedantie van elk weefsel wordt vervangen in de formule:

Z = ρ.v

Op deze manier:

Z_vet = 952 kg/m³ x 1450 m/s = 1.38 x 10⁶ kg/m².S

Z_spier = 1075 kg/m³ x 1590 m/s = 1.71 x 10⁶  kg/m².S

Oplossing B

Om het percentage intensiteit te vinden dat wordt weerspiegeld in de interface van de twee weefsels, is de reflectiecoëfficiënt gegeven door:

R = (z₁ - Z₂))²/(Z₁ +Z₂))²

Hier z_vet = Z₁ en z_spier = Z_2. De reflectiecoëfficiënt is een positieve hoeveelheid, die wordt gegarandeerd door de vierkanten in de vergelijking.

Vervangen en evalueren:

R = (1.38 x 10⁶ - 1.71 x 10⁶ ))²  / (1.38 x 10⁶ + 1.71 x 10⁶ ))² = 0.0114.

Door met 100 te vermenigvuldigen, hebben we het gereflecteerde percentage: 1.14 % van de incidentintensiteit.

- Oefening opgelost 2

Een geluidsgolf heeft een intensiteitsniveau 100 decibel en beïnvloedt normaal het oppervlak van het water. Bepaal het intensiteitsniveau van de overgedragen golf en dat van de gereflecteerde golf.

Kan u van dienst zijn: viskeuze wrijving (kracht): coëfficiënt en voorbeelden

Gegevens:

Water

• Dichtheid: 1000 kg/m³
• Geluidssnelheid: 1430 m/s

Lucht

• Dichtheid: 1.3 kg/m³
• Geluidssnelheid: 330 m/s

Oplossing

Het niveau van de decibelintensiteit van een geluidsgolf wordt aangeduid als L, is dimensieloos en wordt gegeven door de formule:

L = 10 log (i /10^-12))

Aan beide kanten op 10 stijgen:

10 ^L/10 = I /10^-12

Als l = 100, resulteert in:

I/10^-12 = 10¹⁰

De intensiteitseenheden worden gegeven in termen van stroom per gebiedseenheid. In het internationale systeem zijn ze watt/m². Daarom is de intensiteit van de invallende golf:

Je_of = 10¹⁰ . 10^-12 = 0.01 w/m².

Om de intensiteit van de verzonden golf te vinden, wordt de transmissiecoëfficiënt berekend en vervolgens vermenigvuldigd met de invallende intensiteit.

De respectieve impedanties zijn:

Z_water = 1000 kg/m³ x 1430 m/s = 1.43 x 10⁶ kg/m².S

Z_lucht = 1.3 kg/m³ x 330 m/s = 429 kg/m².S

Vervangen en evalueren in:

T = 4Z₁Z₂ /(Z₁ +Z₂))² = 4 × 1.43 x 10⁶ X 429 / (1.43 x 10⁶ + 429)² = 1.12 x 10^-3

Dus de intensiteit van de overgedragen golf is:

Je_T = 1.12 x 10^-3 X 0.01 w/m² = 1.12 x 10^-5 W/m²

Het intensiteitsniveau van de decibel wordt berekend door:

L_T = 10 log (i_T /10^-12) = 10 log (1.12 x 10^-5 / 10^-12) = 70.3 dB

Van zijn kant is de reflectiecoëfficiënt:

R = 1 - t = 0.99888

Hiermee is de intensiteit van de gereflecteerde golf:

Je_R = 0.99888 x 0.01 w/m² = 9.99 x 10^-3 W/m²

En het niveau van intensiteit is:

L_T = 10 log (i_R /10^-12) = 10 log (9.99 x 10^-3 / 10^-12) = 100 dB

Referenties

1. Andriessen, m. 2003. HSC Physics Course. Jacaranda.
2. Baranek, l. 1969. Akoestiek. Tweede druk. Amerikaans Spaans redactioneel.
3. Kinsler, L. 20000000000000000000. Fundamentals of Acoustics. Wiley en zonen.
4. Lowrie, W. 2007. Fundamentele geofysica. 2e. Editie. Cambridge University Press.
5. Wikipedia. Akoestische impedantie. Opgehaald uit: in.Wikipedia.borg.