Wat is het magnetische moment?

Hij Magnetisch moment Het is een vector die de stroom relateert die een beetje of gesloten lus kruist met het gebied van hetzelfde. De module is gelijk aan het product van de intensiteit van de stroom door het gebied, en de richting en richting worden gegeven door de rechterhandregel, zoals weergegeven in figuur 1.

Deze definitie is ongeacht geldig. Wat betreft de eenheid van het magnetische moment, in het internationale systeem van eenheden als het ampère × m is².

Figuur 1. De magnetische momentvector van een willekeurige stroombinding staat loodrecht op zijn vlak en de richting wordt bepaald door de rechterduimregel. Bron: Wikimedia Commons.

In wiskundige termen, het duidt op het magnetische moment van vector met de Griekse teksten μ (Vetgedrukt omdat het een vector is en zich dus onderscheidt van zijn grootte), wordt het uitgedrukt als:

μ = IA N

Waar ik de intensiteit van de stroom is, is A het gebied dat de lus omsluit en N Het is de eenheidsvector (van module gelijk aan 1) die wijst in de richting loodrecht op het vlak van de spase, en waarvan de betekenis wordt gegeven door de regel van de rechterduim (zie figuur 1).

Deze regel is heel eenvoudig: krul de vier vingers van de rechterhand zodat ze de stroom volgen, de duim geeft richting en richting aan van N en daarom het magnetische moment.

De vorige vergelijking is geldig voor een lus. Als er nougas zijn zoals in een spoel, wordt het magnetische moment vermenigvuldigd met n:

μ = nIA N

[TOC]

Magnetisch moment en magnetisch veld

Het is gemakkelijk om uitdrukkingen te vinden voor het magnetische moment van beurten met gewone geometrische vormen:

-Vierkante kant van zij ℓ ℓ: μ = Iℓ² N

-Zijkanten rechthoekige spiraal naar En B: μ = IAB N

-Radio R. Radio Spira: μ = IπR² N

Kan u van dienst zijn: atoomnummer

Dipolo's magnetische veld

Het magnetische veld geproduceerd door de huidige lus of spase lijkt op dat van een staafmagneet en ook dat van de aarde.

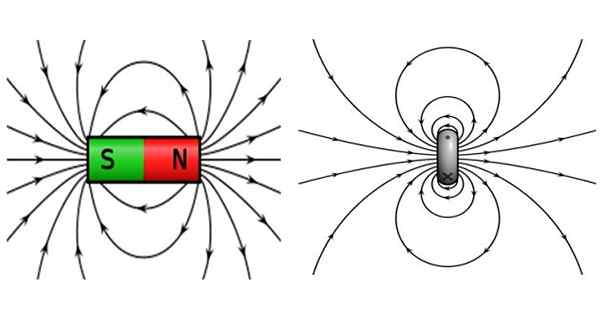Figuur 2. Links links. Bron: Wikimedia Commons.

De barmagneten worden gekenmerkt door Noordpool en Zuidpool te hebben, waar tegengestelde polen worden aangetrokken en dezelfde polen afstoten. De veldlijnen zijn gesloten, verlaten de noordpool en bereiken de zuidpool.

Nu zijn de magnetische polen onafscheidelijk, wat betekent dat als een staafmagneet is verdeeld in twee kleinere magneten, ze hun eigen noord- en zuidpalen blijven hebben. Het is niet mogelijk om de geïsoleerde magnetische polen te hebben, en daarom wordt de staafmagneet genoemd Magnetische dipolo.

Het magnetische veld van een straal R-spiraal r, die een stroom I transporteert, wordt berekend door de biot-savartwet. Voor de punten die behoren tot de symmetrieas (in dit geval de X -as), wordt het veld gegeven door:

Waar μ_of Het is de permeabiliteit van vacuüm. Het veld op punten weg van de spase, waarvoor wordt vervuld dat x >> r, het veld nadert:

Relatie tussen het magnetische veld en het magnetische moment van de dipolo

Inclusief het magnetische moment in de vorige uitdrukking is:

Op deze manier is de intensiteit van het magnetische veld evenredig met het magnetische moment. Merk op dat de intensiteit van het veld afneemt met de afstandskubus.

Deze benadering is van toepassing op elke lus, zolang X groot zijn in vergelijking met de afmetingen.

En aangezien de lijnen van dit veld lijken op die van de barmagneet, is de vergelijking een goed model voor dit magnetische veld en dat van andere systemen waarvan de lijnen vergelijkbaar zijn, zoals: bijvoorbeeld:

Kan u van dienst zijn: absorptie: wat is, voorbeelden en oefeningen opgelost

-Deeltjes in beweging geladen als het elektron.

-Het atoom.

-Aarde en andere planeten en satellieten van het zonnestelsel.

-Sterren.

Effect van een extern veld op de lus

Een zeer belangrijk kenmerk van het magnetische moment is de link naar het koppel dat de luservaring in aanwezigheid van een extern magnetisch veld.

Een elektromotor bevat spoelen waardoor een stroom van veranderende richting doorgaat en dat dankzij de externe veld een turn -effect ervaart. Deze draai zorgt ervoor dat een as bewegen en elektrische energie wordt mechanische energie tijdens het proces.

Koppel op een rechthoekige lus

Stel dat, om de berekeningen te vergemakkelijken, een rechthoekige kanten naar En B, waarvan de normale vector N, uitgaande scherm, aanvankelijk staat het loodrecht op een uniform magnetisch veld B, zoals in figuur 3. De zijkanten van de lus ervaren krachten gegeven door:

F = IL X B

Waar L Het is een magnitude -vector gelijk aan de lengte van het segment en gericht volgens de stroom, en is de intensiteit van dezelfde en B Het is het veld. Kracht staat loodrecht op beide L Zoals het veld, maar niet alle partijen ervaren kracht.

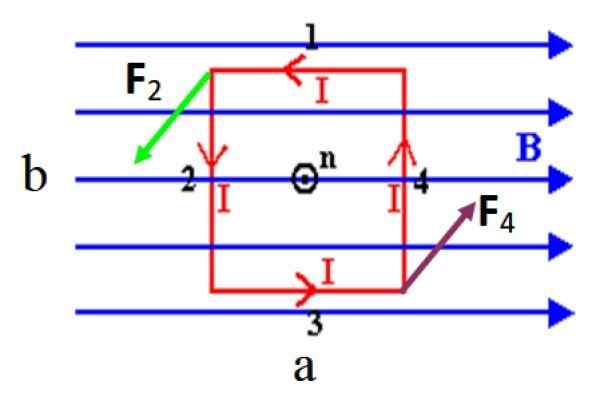figuur 3. Een rechthoekige spiraal die een stroom I in anti -horaire zin transporteert, ervaart een koppel in aanwezigheid van een uniform uniform magnetisch veld. Bron: f. Zapata.

In de getoonde figuur is er geen sterkte aan de korte zijden 1 en 3 voor het parallel aan het veld, onthoud dat het kruisproduct tussen parallelle vectoren nietig is. Lange zijden 2 en 4, die echter loodrecht staan ​​op B, Ze ervaren aangeduidelijke krachten als F₂ En F₄.

Deze krachten vormen zich een paar: Ze hebben dezelfde grootte en richting, maar tegengestelde zintuigen, daarom kunnen ze niet naar de lus in het midden van het veld gaan. Maar ze kunnen het laten roteren, omdat het koppel  τ Dat elke kracht uitoefent, met betrekking tot de verticale as die door het midden van de lus gaat, heeft deze dezelfde richting en betekenis.

Kan u van dienst zijn: cohesiekracht

Volgens de definitie van koppel, waar R Het is de positievector:

τ = R X F

Dus:

τ₂ = τ₄=(A/2) f (+J ))

Individuele knooppunten worden niet geannuleerd, omdat ze dezelfde richting en betekenis hebben, dan worden ze toegevoegd:

τ_netto = τ₂ + τ₄ = A F (+J ))

En als de grootte van de kracht f = ibb, resulteert het:

τ_netto = I⋅a⋅B⋅B (+J ))

Het A⋅B -product is gebied A van de spase, dus IAB is de grootte van het magnetische moment μ. Daarom τ_netto = μ⋅b (+J ))

Het is te zien dat het koppel in het algemeen samenvalt met het vectorproduct tussen de vectoren μ En B:

τ_netto = μ X B

En hoewel deze uitdrukking is afgeleid van een rechthoekige lus, is deze willekeurig geldig voor een platte voet aan de grond.

Het effect van het veld op de lus is een koppel dat de neiging heeft het magnetische moment uit te lijnen met het veld.

Potentiële energie van de magnetische dipool

Om de spiraal of de dipool in het midden van het veld te keren, moet een werk worden uitgevoerd tegen de magnetische kracht, die de potentiële energie van Dipolo verandert. De variatie van energie Δu, wanneer de spiraal draait vanuit de hoek θ_of In de hoek wordt θ gegeven door de integraal:

Als het referentieniveau wordt gekozen als θ_of = π/2:

Δu = -μB cos θ

Die op zijn beurt kunnen worden uitgedrukt als het scalaire product tussen de vectoren B En μ:

Δu = - μ ·B

De minimale potentiële energie in de dipool treedt op wanneer cos θ = 1, wat dat betekent μ En B Ze zijn parallel, de energie is maximaal als ze tegengesteld zijn (θ = π) en is nietig wanneer ze loodrecht zijn (θ = π/2).

Referenties

1. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 5. Elektromagnetisme. Uitgegeven door Douglas Figueroa (USB).
2. Resnick, r. 199999. Fysiek. Vol. 2. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V.
3. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 2. Pearson.
4. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 2. 7e. ED. Cengage leren.
5. Tipler, p. (2006) Natuurkunde voor wetenschap en technologie. 5e ed. Deel 2. Redactioneel teruggekeerd.