Wat is de snij-, stijfheid- of afschuifmodule? (Opgeloste oefeningen)

Hij Module gesneden Beschrijf de reactie van een materiaal op de toepassing van een afschuifinspanning die het vervormt. Andere frequent gebruiksominaties voor de snijmodule zijn afschuiving, schaar, dwarse elasticiteit of tangentiële elasticiteitsmodule.

Wanneer de inspanningen klein zijn, zijn de vervormingen evenredig aan hen, volgens de wet van Hook. Daarom:

Cut -module = snijden/vervorming inspanning

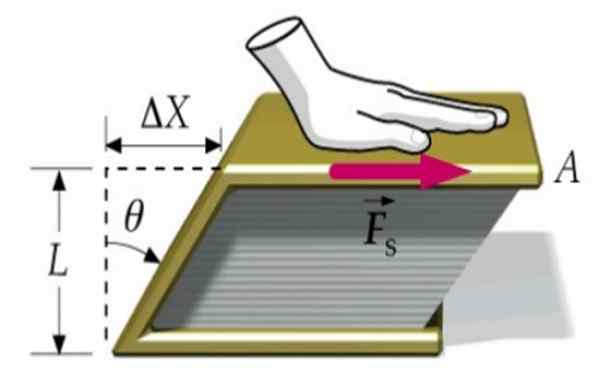
Figuur 1. Een boek is vervormd dankzij de tangentiële kracht FS. Bron: f. Zapata.

Stel dat een kracht wordt uitgeoefend op het deksel van een boek, als de andere gefixeerd op het oppervlak van de tafel. Op deze manier beweegt het boek als geheel niet, maar vervormt het wanneer het bovenste deksel beweegt ten opzichte van de onderste in de hoeveelheid Δx.

Het boek gaat van het hebben van een rechthoekig transversale sectie naar een sectie in de vorm van parallellogram, zoals we in het superieure beeld zien.

Zijn:

τ = f/a

De inspanning of het snijden van spanning, zijnde F de omvang van de uitgeoefende kracht en NAAR Het gebied waarop het handelt.

De veroorzaakte vervorming wordt gegeven door het quotiënt:

Δ = Δx / l

Daarom is de snijmodule, die we als G zullen aangeven,:

Op deze manier is de snijmodule verantwoordelijk voor het meten van de weerstand van de binnenvlakken van het object die evenwijdig zijn aan de toegepaste inspanning.

En omdat Δx / L dimensies mist, zijn de eenheden van G dezelfde als die van de snijspoging, wat de reden is tussen de kracht en het gebied.

In het internationale systeem van eenheden zijn deze eenheden Newton/Square Metro of Pascal, afgekort PA. En in Anglo -saxon -eenheden is het pond /vierkante inch, afgekort psi.

[TOC]

Kan u van dienst zijn: uniforme rechtlijnige beweging: kenmerken, formules, oefeningen

Snijd module voor verschillende materialen

Onder de werking van snijkrachten zoals beschreven, bieden objecten een weerstand vergelijkbaar met die van het boek, waarin de binnenlagen glijden. Dit type vervorming kan alleen optreden in vaste lichamen, die voldoende stijfheid hebben om te verzetten tegen vervormd zijn.

Aan de andere kant bieden vloeistoffen dit soort weerstand niet, maar ze kunnen volume -vervormingen ervaren.

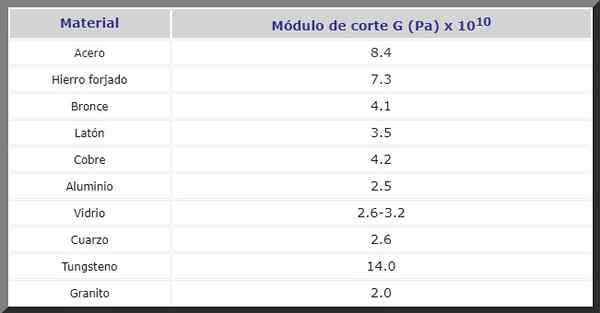
Figuur 2. Bouten in structuren zijn onderhevig aan het snijden van inspanningen. Bron: Pixnio.

Vervolgens hebt u de G -Cut -module in P voor verschillende materialen die vaak worden gebruikt in aanbouw en bij de productie van allerlei machines en reserveonderdelen:

Experimentele maat van de snijmodule

Om de waarde van de snijmodule te vinden, moet u monsters van elk materiaal testen en uw reactie op de toepassing van een snijspoging onderzoeken.

Het monster is een staaf gemaakt met het materiaal, met radio R en lengte L Bekend, dat aan de ene kant wordt vastgesteld, terwijl de andere verbindt met de as van een vrije poelie.

De poelie heeft een touw vastgebonden, aan wiens vrije einde wordt een weeg opgehangen dat een kracht uitoefent F Op de stang door het touw. En deze kracht produceert op zijn beurt een moment M In de staaf, die vervolgens een kleine hoek θ draait.

Een assemblageschema is te zien in de volgende figuur:

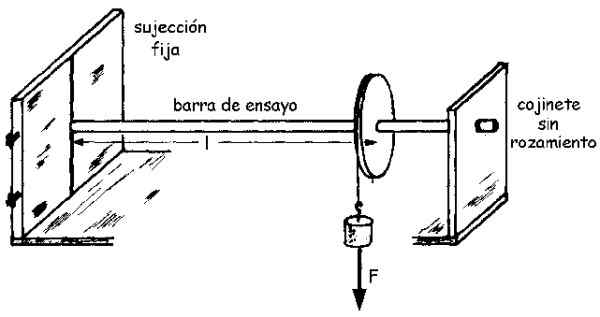figuur 3.- Experimentele assemblage om de afschuifmodule te bepalen of een dunne testbalk te snijden. Bron: Universiteit van Valladolid.

De omvang van het moment M, die we aangeven als M (Zonder BOLD) is gerelateerd aan de hoek die θ is gedraaid door de gesneden module G volgens de volgende vergelijking (deze wordt afgeleid door een eenvoudige integraal):

Omdat de grootte van het moment gelijk is aan het product van de kracht F -module door de straal van de poelie r_P:

Het kan u van dienst zijn: Torricelli Experiment: Atmosferische drukmaatregelen, belang

M = F.R_P

En kracht is het gewicht dat hangt W, Dus:

M = W.R_P

Vervangen in de vergelijking van de grootte van het moment:

Je hebt de relatie tussen gewicht en hoek:

Hoe G te vinden G?

Deze relatie tussen variabelen W En θ Het is lineair, dus de verschillende geproduceerde hoeken worden verschillende gewichten gemeten.

De paren van gewicht en hoek zijn grafieken op een millimeter papier, de beste lijn die door de experimentele punten gaat, wordt aangepast en de helling wordt berekend M van genoemde lijn.

 Van daaruit volgt dat:

Oefeningen met oplossing

- Oefening 1

Een 2 staaf.5 meter lang en radio 4.5 mm is aan één uiteinde gefixeerd. De andere verbindt zich met een 75 cm radiopoelie met een gewicht van 1 1.3 kg. De gedraaide hoek is 9.5e.

Met deze gegevens wordt gevraagd om de snijmodule G van de staaf te berekenen.

Oplossing

Uit de vergelijking:

Gasses G:

En de waarden die in de verklaring worden gegeven, worden vervangen, waardoor alle gegevens in het internationale systeem van eenheden worden uitgesproken als:

R = 4.5 mm = 4.5 x 10 ^-3 M

R_P = 75 cm = 0.075

Om van kilogrammen te gaan (ze zijn eigenlijk kilogrammen - kracht) naar Newton Multiples met 9.8:

W = 1.3 kg-force = 1.3 x 9.8 n = 12.74 n

En ten slotte moeten de graden op radialen zijn:

9.5e = 9.5 x2π /360 radialen = 0.1658 radianen.

Met dit alles heb je:

= 2.237 x 10¹⁰ vader

- Oefening 2

Een gelbube is 30 cm kant. Een van de gezichten is vastgesteld, maar tegelijkertijd wordt een parallelle kracht van 1 N toegepast op het tegenovergestelde gezicht, die dankzij deze beweegt 1 cm (zie het voorbeeld van het boek in figuur 1).

Het kan u van dienst zijn: magnetisatie: orbitaal en spin magnetisch moment, voorbeelden

Er wordt gevraagd om met deze gegevens te berekenen:

a) de omvang van de schuifspanning

b) Unitaire vervorming δ

c) De waarde van de snijmodule

Oplossing voor

De omvang van de schuifspanning is:

τ = f/a

Met:

A = zijde² = (30 x 10^-2 cm)² = 0.09 m²

Daarom:

τ = 1 n / 0.09 m² = 11.1 PA

Oplossing B

Unitaire vervorming is niemand minder dan de waarde van 8, gegeven door:

Δ = Δx / l

De verplaatsing van het gezicht dat aan de kracht wordt onderworpen, is dan 1 cm, dan:

Δ = 1/30 = 0.0333

Oplossing C

De snijmodule en het quotiënt tussen de snijspoging en de vervorming van de eenheid:

G = Snijden/vervorming inspanning

Daarom:

G = 11.1 PA /0.033 = 336.4 PA

Referenties

1. Bier, f. 2010. Materiaalmechanica. McGraw Hill. 5e. Editie.
2. Franco Garcia, aan. Rigide vast. Hoor modulemeting. Opgehaald uit: SC.Ehu.is.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Resnick, r. (1999). Fysiek. Vol. 1. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V.
5. Universiteit van Valladolid. Afdeling natuurkunde van gecondenseerde materie. Selectie van problemen. Hersteld van: www4.druif.is.