Cartografische conische projectiekenmerken, voordelen, nadelen

De Cartografische conische projectie Het wordt gekenmerkt door de punten van een sferisch oppervlak op het oppervlak van een kegel te projecteren, waarvan het hoekpunt zich op de as bevindt die door de polen gaat en raakt of drogen naar de bol. De kegel is een oppervlak dat in een vlak kan worden geopend, waardoor een hoeksector wordt gevormd en zonder de geprojecteerde lijnen erop te vervormen.

De wiskundige Johann Heinrich Lambert (1728 - 1777) was degene die deze projectie heeft bedacht en voor het eerst in zijn boek verscheen Freye perspectief (1759), waar hij verschillende theorieën en reflecties over projecties verzamelde.  

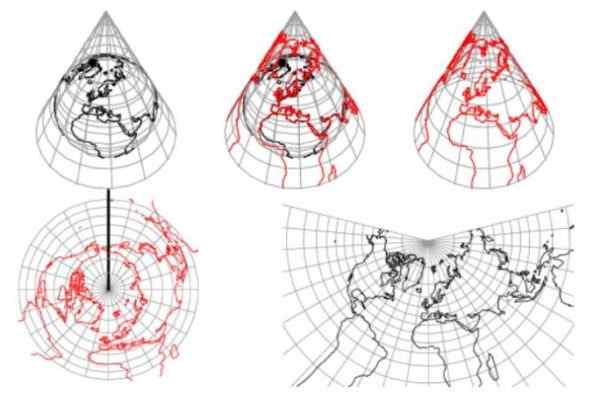
Figuur 1. Conische projectie. Bron: Weisstein, Eric W. “Kona -projectie.”Van Mathworld-a Wolfram Web Resource.

In de conische projecties van het aardoppervlak worden de meridianen radiale lijnen gericht op het hoekpunt, met dezelfde hoekafstand en worden de terrestrische parallellen concentrische cirkelvormige bogen met de hoekpunt.

Figuur 1 laat zien dat de conische projectie niet toestaat dat beide hemisferen worden weergegeven. Bovendien wordt duidelijk opgemerkt dat afstanden worden vervormd van parallellen die de kegel onderscheppen. 

Vanwege deze redenen wordt dit type projectie gebruikt om middelgrote breedtegebieden te vertegenwoordigen, uitgebreid van oost naar west en kleiner noord-zuid. Dat is het geval van de continentale regio van de Verenigde Staten.

[TOC]

Voordelen

De aarde kan een radiosfeer van 6378 km benaderen, gezien het feit dat alle terrestrische en watermassa op die grote sfeer zijn. Het gaat over het omzetten van dit oppervlak, dat een object bedekt in drie dimensies, zoals een bol, in een ander object in twee dimensies: een platte kaart. Dit brengt het ongemak dat het gebogen oppervlak vervormd is en het in het vliegtuig wil projecteren.

Kan je van dienst zijn: Júcar River

Cartografische projecties, zoals conische projectie, proberen dit probleem op te lossen met het lagere mogelijke verlies van nauwkeurigheid. Daarom zijn er verschillende opties om een ​​projectie te maken, volgens de kenmerken die worden benadrukt.

Onder deze belangrijke kenmerken zijn afstanden, oppervlak, hoeken en meer. De beste manier om ze allemaal te houden, is het land op schaal vertegenwoordigen. Maar dit is niet altijd praktisch.

Overal een wereldbol transport is niet eenvoudig, omdat deze volume bezet. Noch kan het hele aardoppervlak tegelijkertijd worden gezien en het is onmogelijk om alle details in een schaalmodel te reproduceren.

We kunnen ons voorstellen dat de planeet een sinaasappel is, de sinaasappel schillen en de schil op de tafel spreiden, in een poging het beeld van het oranje oppervlak opnieuw op te bouwen. Het is duidelijk dat er in het proces veel informatie zal verloren gaan.

De projectieopties zijn als volgt:

- Projecteren op een vliegtuig of

- Op een cilinder, die kan worden ontwikkeld als een rechthoekig vlak.

- Eindelijk over een kegel.

Het conische projectiesysteem heeft het voordeel dat nauwkeurig is ten opzichte van de parallellen die zijn gekozen om de projectiekegel te onderscheppen.

Bovendien handhaaft het vrijwel intacte oriëntatie in de meridianen, hoewel het de schaal een beetje overal kan vervormen voor de breedtegraden van standaard- of referentie -parallellen. Daarom is het gepast om zeer uitgebreide of continentlanden te vertegenwoordigen.

De opeenvolgende conische projectie

Het is het conische projectiesysteem dat oorspronkelijk werd gebruikt door Ptolemy, een Griekse geograaf die tussen 100 en 170 d jaar leefde. C. Vervolgens werd het in 1745 verbeterd.

Het kan je van dienst zijn: Western Cordillera de Colombia

Het wordt vaak gebruikt in de atlas van de gebieden met tussenliggende breedtegraden. Het is geschikt om gebieden te tonen met een paar graden van breedtegraad, en die behoren tot een van de equatoriale hemisferen.

In deze projectie zijn de afstanden waar in de meridianen en in de twee standaard parallellen, dat wil zeggen de parallellen die zijn gekozen om te onderscheppen met de projectiekegel. 

In de opeenvolgende conische projectie strekt zich een punt op de bol radiaal uit tot zijn kruising met de raaklijn of secant kegel, die als een projectiecentrum het midden van de bol neemt.

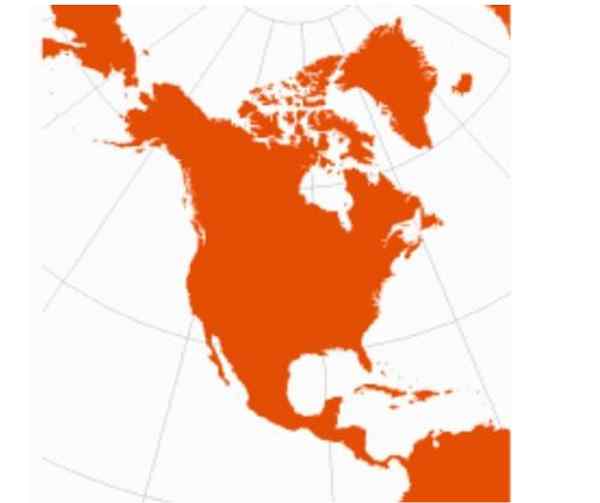Figuur 2. Noord -Amerika met een gelijke conische projectie. Bron: radicale cartografie.

Nadelen

Het belangrijkste nadeel van conische projectie is dat het niet van toepassing is op equatoriale regio's.

Bovendien is conische projectie niet geschikt om grote regio's in kaart te brengen, maar eerder bepaalde gebieden, zoals Noord -Amerika.

Albert's conische projectie

Gebruik twee standaard parallellen en bewaar het gebied, hoewel niet de schaal en vorm. Dit type conische projectie werd gepresenteerd door h. C. Albers in 1805.

Alle gebieden op de kaart zijn evenredig met de overeenkomstige op aarde. In beperkte regio's zijn adressen relatief nauwkeurig. De afstanden komen overeen met die van het sferische oppervlak op de standaard parallel.

In de Verenigde Staten wordt dit projectiesysteem voor kaarten die de limieten van de staten van de Unie laten zien, gebruikt, waarvoor ze worden gekozen als standaard parallellen op 29,5º N en 45,5º N resulterend als maximale fout van schaal 1, 25%.

Kaarten die met deze projectie zijn gemaakt, behouden niet de hoeken die overeenkomen met die van de bol, noch behouden het perspectief of de equidistance.

Kan u van dienst zijn: Petrology

Conische projectie volgens Lambert

Het werd in 1772 voorgesteld door de wiskundige en Zwitserse geograaf met dezelfde naam. Het belangrijkste kenmerk is dat het een raaklijn of secant kegel op de sfeer gebruikt en de projectie de invariant van de hoeken behoudt. Deze kwaliteiten maken het erg nuttig in navigatie luchtvaartbrieven. 

De Geological Service (USGS) van de Verenigde Staten maakt gebruik van de conische projectie van Lambert. In deze projectie zijn de afstanden waar gedurende de standaard parallellen waar.

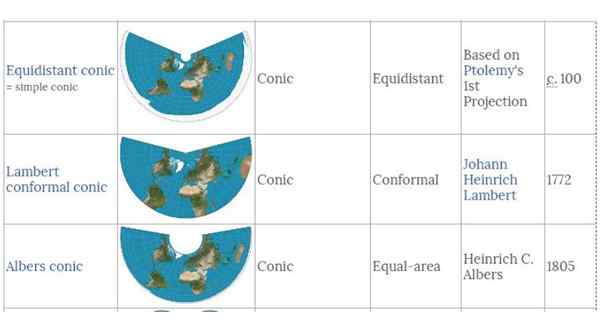figuur 3. Verschillende conische projecties van het noordelijk halfrond, aan de rechterkant, de scheppingsdatum. Bron: Wikimedia Commons.

In de conische projectie van Lambert blijven de adressen redelijk nauwkeurig. De gebieden en vormen zijn weinig vervormd in posities in de buurt van standaard parallellen, maar de wijziging van de vorm en het gebied neemt toe met scheiding daarop. 

Omdat het doel van deze projectie is om aanwijzingen en hoeken te handhaven die gelijk zijn aan de originelen op de bol of ellipsoïde, is er geen geometrische methode om het te verkrijgen, in tegenstelling tot de opeenvolgende Ptolemy -projectie.

Het is eerder een analytische projectiemethode, gebaseerd op wiskundige formules.

De USGS -basiskaarten voor de 48 continentale verklaringen gebruiken standaard 33ºN en 45ºN parallellen, waardoor een maximale fout in de 2,5% kaarten wordt gooit.

Voor navigatiekaarten in Alaska zijn de gebruikte basisparallellen 55ºN en 65ºN. Aan de andere kant, de National Atlas of Canada USA 49ºN en 77ºN.

Referenties

1. Geohunter. Het Lambert Conformal Conic Project. Hersteld van: Geo.Jager.Cuny.Edu
2. Gisgografie. Conische projectie: Lambert, Albers en Polykonic. Hersteld van: gisgeografie.com
3. Gisgografie. Wat zijn kaartprojecties? Hersteld van: gisgeografie.com
4. USGS. Kaartprojecties. Hersteld van: ICSM.Gov.Au
5. Weisstein, Eric W. “Albers gelijk AEA Conic Project.”Hersteld van: Mathworld.Wolfraam.com
6. Weisstein, Eric W. "Conic Projection" hersteld van: Mathworld.Wolfraam.com
7. Weisstein, Eric W. "Lambert Conformal Conic Project" hersteld van: Mathworld.Wolfraam.com
8. Wikipedia. Lijst met kaartprojecties. Opgehaald uit: in.Wikipedia.com