Startpagina
Wiskunde
Beperk eigenschappen (met voorbeelden)

Wiskunde

Beperk eigenschappen (met voorbeelden)

1284
350
Irving McClure I

De Beperk eigenschappen Ze zijn de set van algebraïsche regels en procedures die worden gebruikt om ze te bepalen. Het limietconcept is essentieel voor de berekening en het vinden van de waarde ervan hoeft geen gecompliceerde taak te zijn, op voorwaarde dat de eigenschappen ervan gemakkelijk worden behandeld.

Hieronder is een lijst met de belangrijkste, vergezeld van voorbeelden van toepassingen.

De limieten en de eigenschappen zijn de basis van de berekening. Een zeer speciale limiet wordt weergegeven in de figuur: de afgeleide van een F (x) -functie

Laat B, C, N, A en B reële getallen, en F En G Dergelijke functies die het volgende verifiëren:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Dan heb je de volgende eigenschappen:

1. Directe vervangingslimiet

In eerste instantie kan de limiet van een functie f wanneer x → c direct wordt berekend ter vervanging van x = c in de functie. Als de functie bestaat bij x = c, is de limiet:

$\lim_x \rightarrow c f(x)=f(c)$ Maar niet noodzakelijkerwijs moet de functie worden gedefinieerd bij x = c zodat de limiet bestaat. Het idee is om zoveel te benaderen als u wilt bij de waarde van x = c en te zien wat er gebeurt met de functie in dat geval.

Voorbeeld

Zoek de limiet van f (x) = x² Wanneer x → 4

Oplossing

De limiet lost eenvoudig op door x = 4 te vervangen in f (x) = x², Omdat er geen ongemak is bij het uitvoeren van de operatie:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Uniekheid van de limiet

Als de limiet van een functie f (x) wanneer x → c bestaat en L is, is de limiet uniek.

Daarom zijn de laterale limieten, die zijn die wanneer x → c^- (Lees "x neigt naar C van links") en wanneer x → c⁺(Het luidt: "X heeft de neiging C aan de rechterkant"), beide bestaan en hebben dezelfde waarde L, zelfs als de functie niet is gedefinieerd in x = c.

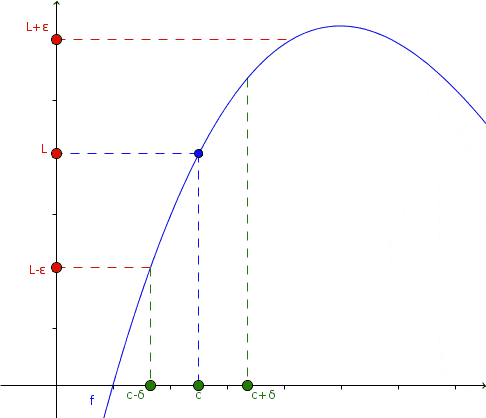In deze animatie wordt het concept van limiet gepresenteerd: wanneer X de neiging heeft om een bepaalde waarde C te hebben, zowel aan de linkerkant als rechts nadert, heeft de waarde van de functie de neiging L. Niet noodzakelijkerwijs wordt de functie gedefinieerd in x = c. Bron: Wikimedia Commons.

In de animatie wordt deze aanpak waargenomen en wat er in dat geval met de functie gebeurt: of deze aan de linkerkant en rechts naar X = C nadert, de waarde van de functie is op zijn beurt dicht bij L.

Kan u van dienst zijn: minimale vierkanten

Wiskundig drukt op deze manier uit:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ De laterale limieten staan toe om te weten wanneer een limiet bestaat of niet, want als ze niet bestaan of als ze verschillen, is het zeker dat de limiet van de functie wanneer x → c niet bestaat.

Voorbeeld

Bereken de limiet van f (x) wanneer x → 1 als deze bestaat, waarbij f (x) wordt gegeven door:

Oplossing

Dit is een functie door onderdelen of gedefinieerd in stukken, die bestaat uit regel 4 -x voor de waarden van x < 1 y en la parábola 4 - x² Wanneer x gelijk is aan 1 of groter dan 1.

We kunnen X = 1 van links benaderen, in dit geval is het deel van de functie die geldig is voor X genomen<1:

Aangezien de laterale limieten hetzelfde zijn, volgt hieruit dat de limiet van de functie wanneer x → 1 bestaat en 3 waard is.

3. Constante

De limiet van een constante is de waarde van genoemde constante, ongeacht de waarde waartoe de variabele neigt:

$\lim_x\rightarrow cb=b .$

Voorbeeld

Berekenen:

$\lim_x\rightarrow 1\pi$ Oplossing

$\lim_x\rightarrow 1\pi= \pi$

4. Identiteitsfunctielimiet

Als f (x) = x, is het altijd vervuld dat:

$\lim_x\rightarrow cx=c$

Voorbeeld

Berekenen:

$\lim_x\rightarrow 2x$ Oplossing

$\lim_x\rightarrow 2x=2$

5. Productlimiet van een constante door een functie

In dit geval gaat de constante uit de limiet en gaat het om het te vermenigvuldigen, zoals deze:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Voorbeeld

Bereken, als het bestaat, de volgende limiet:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Oplossing

De constante 5 is buiten het vermenigvuldigen tot de limiet en de vervangingseigenschap wordt toegepast:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Somlimiet

De limiet van de som van twee functies F En G Het is de som van de limieten:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Voorbeeld

Zoek de volgende limiet als deze bestaat:

Kan u van dienst zijn: theorie instellen: kenmerken, elementen, voorbeelden, oefeningen

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Oplossing

De eigenschap van de som van de limieten wordt eerst toegepast en vervolgens die van directe vervanging, omdat de bewerkingen geen moeilijkheid hebben:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Aftrekkingslimiet

In het geval van de limiet van de aftrekking van twee functies, ga op een analoge manier die voor de som: de limiet van de aftrekken is de aftrekking van de limieten:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Voorbeeld

Bereken de volgende limiet:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Oplossing

De eigenschap van de aftrekklimiet van twee functies wordt toegepast en vervolgens de directe vervanging, omdat alle bewerkingen zonder probleem kunnen worden uitgevoerd:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Productlimiet

De productlimiet van twee functies F En G Het is het product van de limieten:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Voorbeeld

Bereken deze limiet:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Oplossing

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Verhouding van het quotiënt

De limiet van de verhouding van twee functies F En G Het is het quotiënt van de limieten, op voorwaarde dat de limiet van g (x) wanneer x → c verschilt van 0, omdat de divisie door 0 niet is gedefinieerd. Dus:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Voorbeeld

Bereken, als het bestaat, de waarde van de volgende limiet:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Oplossing

In eerste instantie wordt de eigenschap Property Limit toegepast om het quotiënt van de limieten te verkrijgen:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

De vervangingseigenschap wordt nu toegepast om elke limiet te vinden:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

En omdat b ≠ 0 is de gezochte limiet het quotiënt A/B:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Begrenzing

De limiet van een kracht van exponent n is gelijkwaardig aan de limiet die wordt verhoogd tot genoemde macht, als volgt:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Case 1: Limiet van een X -stroom

Als u bijvoorbeeld de limiet van een X -vermogen hebt, resulteert dan:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

Volgens eigenschap 4 is deze limiet:

Kan u van dienst zijn: numerieke analogieën: typen, toepassingen en oefeningen

$\lim_x \rightarrow c x^n=c^n$

Case 2: Root Limit

Een n-deze wortel kan worden geschreven in de vorm van een fractionele exponent, vandaar:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Belangrijk: Als de root -index gelijk is, is het noodzakelijk dat de limiet van f (x) wanneer x → c groter is dan of gelijk is aan 0, omdat er geen echte paren van negatieve hoeveelheden zijn.

Voorbeelden

Bepaal, het toepassen van de vorige eigenschappen, de volgende limieten als ze bestaan:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Oplossing voor

Door eigendom van de limiet van een bevoegdheid en directe substitutie wordt deze verkregen:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Oplossing B

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

elf. Begrenzing

Om de limiet van een basis exponentiële B en exponent f (x) te vinden, moet de basis van de functie van de functie f (x) als volgt worden verhoogd:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Voorbeeld

Zoek of er de volgende limiet is:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Oplossing

In deze limiet is de basis het nummer E en de functie f (x) = x², Daarom moet u eerst de X -limiet berekenen² Wanneer X neigt naar 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Vervolgens wordt de eigenschap van de exponentiële limiet toegepast:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Exponentiële potentiële functielimiet

De limiet wanneer x → c van een functie f (x), die op zijn beurt is verhoogd tot een andere functie g (x) wordt uitgedrukt door:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Voorbeeld

Bereken de volgende limiet, als deze bestaat:

$\lim_x \rightarrow -1 (x-1)^^2x$

Oplossing

Om de vorige eigenschap toe te passen, worden ze eerst geïdentificeerd f (x) = x-1 en g (x) = 2x en vervolgens worden de respectieve limieten berekend:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Eindelijk:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referenties

Ayres, f. 20000000000000000000. Berekening. 5ed. MC Graw Hill.
Leithold, l. 1992. Berekening met analytische geometrie. Harla, s.NAAR.
Gratis wiskundeteksten. Grenzen. Hersteld van: wiskunde.Liibretexts.borg.
Mathemovil. Wetten en beperken eigenschappen. Hersteld van: Matemovil.com.
Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
Purcell, E. J., Varberg, D., & Rigdon, s. EN. (2007). Berekening. Mexico: Pearson Education.
Universe -formules. Beperk eigenschappen. Hersteld van: UniversOFormulas.com

Beperk eigenschappen (met voorbeelden)

1. Directe vervangingslimiet

Voorbeeld

Oplossing

2. Uniekheid van de limiet

Voorbeeld

Oplossing

3. Constante

Voorbeeld

Oplossing

4. Identiteitsfunctielimiet

Voorbeeld

Oplossing

5. Productlimiet van een constante door een functie

Voorbeeld

Oplossing

6. Somlimiet

Voorbeeld

Oplossing

7. Aftrekkingslimiet

Voorbeeld

Oplossing

8. Productlimiet

Voorbeeld

Oplossing

9. Verhouding van het quotiënt

Voorbeeld

Oplossing

10. Begrenzing

Case 1: Limiet van een X -stroom

Case 2: Root Limit

Voorbeelden

Oplossing voor

Oplossing B

elf. Begrenzing

Voorbeeld

Oplossing

12. Exponentiële potentiële functielimiet

Voorbeeld

Oplossing

Referenties

Beste artikelen

Welke studies logica?

Logica studies hoe redeneren en argumenten kunnen evalueren. Stelt het gebruik van redelijke of corr...

Welke studies ornithologie?

Welke studies ornithologie? Ornithologie is de wetenschap die wordt beoefend door die geliefden en v...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Uniekheid van de limiet

$\lim_x\rightarrow 1\pi$ Oplossing

$\lim_x\rightarrow 2x$ Oplossing

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Voorbeeld

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Oplossing

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Oplossing

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Oplossing

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Voorbeeld

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Oplossing

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Case 1: Limiet van een X -stroom

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Oplossing

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referenties