Niet -lineaire programmeermethoden en oefeningen

De Niet -lineair programmeren Het is het proces van het optimaliseren van een functie die afhankelijk is van verschillende onafhankelijke variabelen, die op hun beurt zijn onderworpen aan beperkingen.

Als een of meer van de beperkingen, of als de functie te maximaliseren of te minimaliseren (opgeroepen Objectieve functie), wordt niet uitgedrukt als een lineaire combinatie van de variabelen, dus er is een niet -lineair programmeringsprobleem.

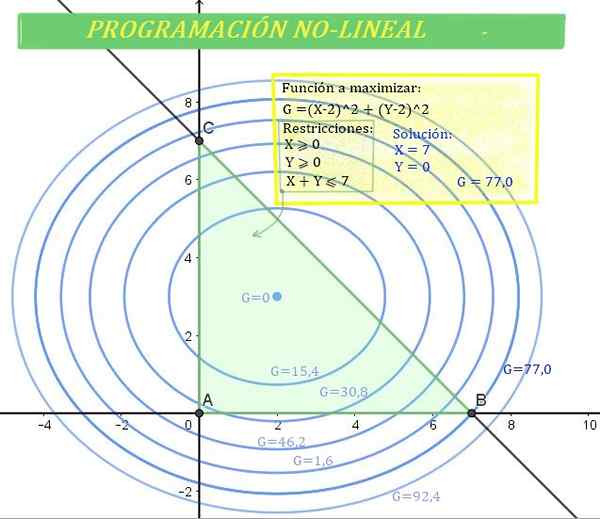
Figuur 1. Niet -lineair programmeringsprobleem (NLP). waarin G de functie (niet-lineair) is om te optimaliseren in het groene gebied, bepaald door de beperkingen. Bron: f. Zapata.

En daarom kunnen de procedures en methoden voor lineair programmeren niet worden gebruikt.

De goed bekende methode kan bijvoorbeeld niet worden gebruikt Simplex, die alleen van toepassing is wanneer de objectieve functie en beperkingen allemaal lineaire combinatie zijn van de variabelen van het probleem.

[TOC]

Lineaire programmeermethoden

Voor niet-lineair programmeren zijn de belangrijkste methoden die moeten worden gebruikt: 

1.- Grafische methoden.

2.- Lagrange -vermenigvuldigers om de grens van het oplossingsgebied te verkennen.

3.- Gradiëntberekening om de uiteinden van de objectieve functie te verkennen.

4.- De dalende stappenmethode, om de nul gradiëntpunten te vinden.

5.- Gemodificeerde methode van Lagrange-multiplicatoren (met de toestand van Karush-Kuhn-Tucker).

Voorbeeld van oplossing met grafische methode

Een voorbeeld van een oplossing met de grafische methode is wat te zien is in figuur 2:

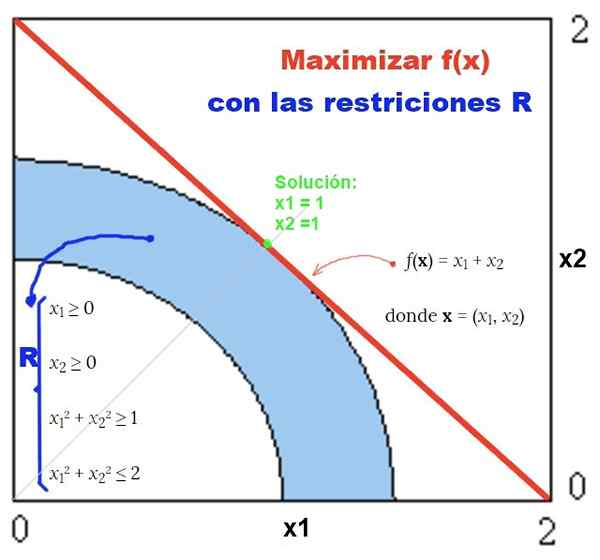Figuur 2. Voorbeeld van niet-lineair probleem met niet-lineale beperkingen en zijn grafische oplossing. Bron: f. Zapata.

Opdrachten

- Oefening 1 (grafische methode)

De winst G van een bepaald bedrijf is afhankelijk van het verkochte bedrag van product X en het verkochte bedrag van het product en bovendien wordt de winst bepaald door de volgende formule:

Kan u van dienst zijn: geconjugeerd binomiaal: hoe het is opgelost, voorbeelden, oefeningen

G = 2 (x - 2)² + 3 (en - 3)²

Het is bekend dat de hoeveelheden X en Y de volgende beperkingen hebben:

X≥0; Y≥0 en x + en ≤ 7

Bepaal de waarden van X en Y die de maximale versterking produceren.

figuur 3. De winst van het bedrijf kan wiskundig worden gemodelleerd om de maximale winst te vinden door niet -lineair programmeren. Bron: Pixabay.

Oplossing 

In dit probleem is de objectieve functie niet -lineair, terwijl de ongelijkheden die de beperkingen definiëren zijn. Het is een probleem van Niet -lineair programmeren.

Voor de oplossing van dit probleem zal de grafische methode worden gekozen.

Ten eerste zal het oplossingsgebied worden bepaald, dat wordt gegeven door de beperkingen.

Als x≥0; Y≥0, de oplossing moet in het eerste kwadrant van het XY -vlak zoeken, maar zoals bovendien moet worden vervuld dat x + y ≤ 7, de oplossing is in de onderste semiplane van de lijn x + y = 7.

Het oplossingsgebied is de kruising van het eerste kwadrant met de onderste semiplane van de lijn, die aanleiding geeft tot een driehoekig gebied waar de oplossing zich bevindt. Is hetzelfde als aangegeven in figuur 1.

Aan de andere kant kan Gain G ook worden weergegeven in het Cartesiaanse vlak, omdat de vergelijking die van een ellips met centrum is (2,3).

De ellips wordt getoond in figuur 1 voor verschillende G -waarden. Een hogere waarde van G, grotere winst.

Er zijn oplossingen die tot de regio behoren, maar niet de maximale waarde G geven, terwijl anderen, zoals G = 92.4, zijn uit de groene zone, dat wil zeggen de oplossingszone.

Vervolgens komt de maximale waarde van G, zodat x e y behoort tot het oplossingsgebied overeen met: 

Kan u van dienst zijn: theoretische waarschijnlijkheid: hoe u het uit kunt krijgen, voorbeelden, oefeningen

G = 77 (maximale versterking), die optreedt voor x = 7 e y = 0. 

Interessant is dat de maximale winst optreedt wanneer de hoeveelheid productverkoop is en nietig is, terwijl de hoeveelheid product X de grootst mogelijke waarde bereikt.

- Oefening 2 (analytische methode: Lagrange -multiplicatoren) 

Zoek de oplossing (x, y) die de functie f (x, y) = x maakt² + 2 en² maximaal zijn in regio g (x, y) = x² + En² - 1 = 0.

Oplossing

Het is duidelijk een niet-lineair programmeerprobleem, omdat zowel de objectieve functie f (x, y) als de beperking g (x, y) = 0, geen lineaire combinatie zijn van de variabelen x en y.

De methode LaGrange Multipliers zal worden gebruikt, die eerst de functie van LaGrange L (X, Y, λ) moet definiëren:

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 en² - λ (x² + En² - 1) 

Waarbij λ een parameter wordt genoemd Lagrange -multiplier.

Om de extreme waarden van de objectieve functie f te bepalen, in het oplossingsgebied gegeven door de beperking G (x, y) = 0, worden deze stappen gevolgd:

-Zoek de gedeeltelijke derivaten van de functie van LaGrange L, met betrekking tot X, Y, λ.

-Nul elke afgeleide.

Hier de volgorde van deze bewerkingen:

1. ∂l/∂x = 2x - 2λx = 0
2. ∂l/∂y = 4y - 2λy = 0
3. ∂l/∂λ = -(x² + En² - 1) = 0

Mogelijke systeemoplossingen

Een mogelijke oplossing van dit systeem is λ = 1 om te voldoen aan de eerste vergelijking, in welk geval y = 0 om de tweede te ontmoeten.

Deze oplossing impliceert dat x = 1 of x = -1 zodat aan de derde vergelijking is voldaan. Op deze manier zijn twee S1- en S2 -oplossingen verkregen:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Het andere alternatief is dat λ = 2 voor de tweede vergelijking moet worden voldaan, ongeacht de waarde en.

Het kan u van dienst zijn: Fermat Limit: wat bestaat en oefeningen opgelost

In dit geval is de enige manier om aan de eerste vergelijking te voldoen, dat x = 0. Gezien de derde vergelijking, zijn er slechts twee mogelijke oplossingen, die we S3 en S4 zullen noemen:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

Om te weten welke of welke van deze oplossingen de objectieve functie maximaliseren, gaat u verder met vervangen in f (x, y):

S1: F (1, 0) = 1² + 2.0² = 1

S2: F (-1, 0) = (-1)² + 2.0² = 1

S3: F (0, 1) = 0² + 2.1² = 2

S4: F (0, -1) = 0² + eenentwintig)² = 2

We concluderen dat de oplossingen die F maximaliseren, wanneer x en y behoren tot de omtrek G (x, y) = 0 S3 en S4 zijn.

De paren van waarden (x = 0, y = 1) y (x = 0, y = -1) maximaliseren f (x, y) in het oplossingsgebied G (x, y) = 0.

- Oefening 3 (NULL DIRECT)

Zoek oplossingen (x, y) voor de objectieve functie:

f (x, y) = x² + 2 en²

Maximaal zijn in regio g (x, y) = x² + En² - 1 ≤ 0.

Oplossing

Deze oefening is vergelijkbaar met Oefening 2, maar het oplossingsgebied (of beperking) strekt zich uit tot het binnengebied van de omtrek g (x, y) = 0, dat wil zeggen de cirkel g (x, y) ≤ 0. Dit omvat de omtrek en de innerlijke regio.

De grensoplossing was al bepaald in Oefening 2, maar het is noodzakelijk om de binnenregio te verkennen.

Om dit te doen, moet de gradiënt van de functie f (x, y) worden berekend en gelijk aan nul, om te zoeken naar extreme waarden in het oplossingsgebied. Dit is gelijk aan het berekenen van de gedeeltelijke derivaten van F ten opzichte van X en respectievelijk en het egaliseren van nul:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Dit vergelijkingssysteem heeft de enige oplossing (x = 0, y = 0) die behoort tot cirkel g (x, y) ≤ 0.

Deze waarde vervangen in functie F Resultaten:

f (0, 0) = 0

Concluderend, de maximale waarde die de functie in het oplossingsgebied neemt, is 2 en treedt op op de rand van het oplossingsgebied, voor waarden (x = 0, y = 1) y (x = 0, y = -1).

 Referenties

1. Avriel, m. 2003. Niet -lineaire programmering. Dover publiceren.
2. Bazara's. 1979. Niet -lineaire programmering. John Wiley & Sons.
3. Bertsekas, D. 199999. Niet -lineaire programmering: 2e editie. Athena wetenschappelijk.
4. Nocedal, J. 199999. Numerieke optimalisatie. Springer-Verlag.
5. Wikipedia. Niet -lineair programmeren. Hersteld van: is.Wikipedia.com