Opmerkelijke producten

Wat zijn opmerkelijke producten?

Opmerkelijke producten zijn algebraïsche bewerkingen, waar vermenigvuldigingen van polynomen worden uitgedrukt, die niet traditioneel hoeven te worden opgelost, maar met behulp van bepaalde regels kunnen de resultaten van hetzelfde worden gevonden.

Polynomen worden vermenigvuldigd met of het daarom mogelijk is dat ze veel termen en variabelen hebben. Om het proces kort te maken, worden de regels van de opmerkelijke producten gebruikt, die vermenigvuldigingen mogelijk maken zonder de term voor termijn te gaan.

Opmerkelijke producten en voorbeelden

Elk opmerkelijk product is een formule die het gevolg is van een factorisatie, samengesteld uit polynomen van verschillende termen zoals binomials of trinomials, factoren genoemd.

De factoren vormen de basis van een kracht en hebben een exponent. Wanneer de factoren zich vermenigvuldigen, moeten de exponenten worden toegevoegd.

Er zijn verschillende opmerkelijke productformules, sommige worden meer gebruikt dan andere, afhankelijk van polynomen, en zijn de volgende:

Vierkant binomiaal

Het is de vermenigvuldiging van een binomiaal op zichzelf, uitgedrukt in de vorm van macht, waar de termen worden toegevoegd of afgetrokken:

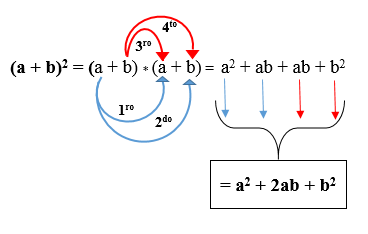
naar. Vierkante som binomiaal: Het is gelijk aan het vierkant van de eerste term, plus het dubbele van het product van de voorwaarden, plus het kwadraat van de tweede termijn. Het wordt als volgt uitgedrukt:

(A + B)² = (a + b) _* (A + B).

In de volgende figuur kunt u zien hoe het product is ontwikkeld volgens de bovengenoemde regel. Het resultaat wordt Trinomial van een perfect vierkant genoemd.

voorbeeld 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Voorbeeld 2

(4a + 2b) = (4a)² + 2 (4e _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

B. Binomiale van een vierkante aftrekking: Dezelfde regel van het binomiale van een bedrag wordt toegepast, alleen dat in dit geval de tweede termijn negatief is. De formule is als volgt:

(A - b)² = [(a) + (- b)]²

Kan u van dienst zijn: numerieke analogieën: typen, toepassingen en oefeningen

(A - b)² = a² +2e _* (-b) + (-b)²

(A - b)²   = A² - 2AB + B².

voorbeeld 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Geconjugeerde binomialsproduct

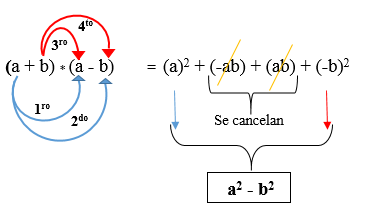
Twee binomials zijn geconjugeerd wanneer de tweede voorwaarden van elk verschillende tekenen zijn, dat wil zeggen, die van de eerste is positief en die van de tweede negatieve of vice versa. Het wordt opgelost door elk monomiaal kwadraat te verhogen en afgetrokken. De formule is als volgt:

(A + B) _* (A - b)

In de volgende figuur wordt het product van twee geconjugeerde binomials ontwikkeld, waar wordt opgemerkt dat het resultaat een verschil van vierkanten is.

voorbeeld 1

(2a + 3b) (2a - 3b) = 4a² + (-6ab) + (6 ab) + (-9b²))

(2a + 3b) (2a - 3b) = 4a² - 9B².

Product van twee binomials met een gemeenschappelijke term

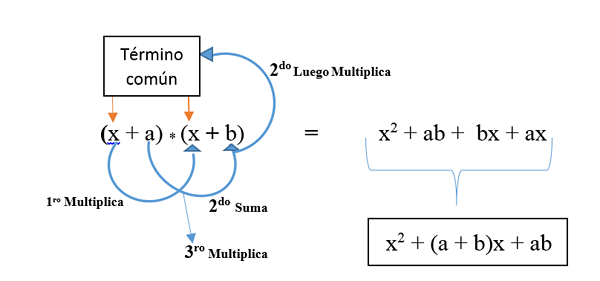
Het is een van de meest complexe en weinig gebruikte opmerkelijke producten omdat het een vermenigvuldiging is van twee binomials met een gemeenschappelijke term. De regel geeft het volgende aan:

• Het vierkant van de gemeenschappelijke term.
• Plus de som de termen die niet gebruikelijk zijn en vermenigvuldig ze vervolgens met de gemeenschappelijke term.
• Plus de som van de vermenigvuldiging van de termen die niet gebruikelijk zijn.

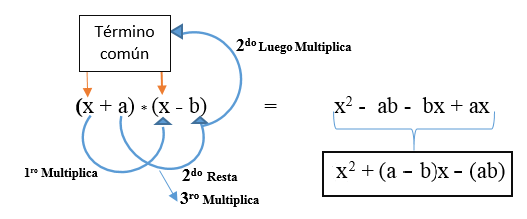
Het wordt weergegeven in de formule: (x + a) _* (x + b) en wordt ontwikkeld zoals weergegeven in de afbeelding. Het resultaat is een niet -perfect vierkant trinomiaal.

voorbeeld 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Er is de mogelijkheid dat de tweede term (de verschillende term) negatief is en de formule als volgt is: (x + a) _* (x - b).

Voorbeeld 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Het kan ook het geval zijn dat beide verschillende termen negatief zijn. Uw formule zal zijn: (x - a) _* (x - b).

Kan u van dienst zijn: Lamy Stelling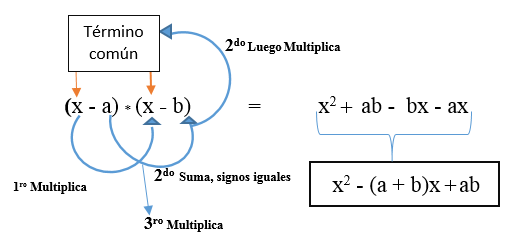

Voorbeeld 3

(3B - 6) _* (3B - 5) = (3B _* 3B) + (-6 - 5)_* (3B) + (-6 _* -5)

(3B - 6) _* (3B - 5) = 9B² + (-elf) _* (3B) + (30)

(3B - 6) _* (3B - 5) = 9B² - 33B + 30.

Vierkant polynoom

In dit geval zijn er meer dan twee termen en om het te ontwikkelen, wordt elk gesneden en worden ze samen met twee keer de vermenigvuldiging van de ene term met de andere; De formule is: (A + B + C)² En het resultaat van de operatie is een trinomiaal kwadraat.

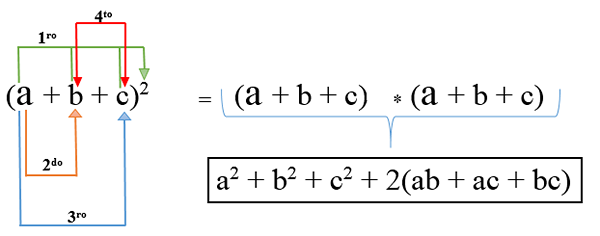
voorbeeld 1

(3x + 2y + 4z)² = (3x)² + (2 en)² + (4Z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16Z² + 12xy + 24xz + 16yz.

Kubus binomiaal

Het is een complex opmerkelijk product. Om het te ontwikkelen, wordt de binomiale als volgt vermenigvuldigd met zijn vierkant:

naar. Voor binomiaal naar de kubus van een som:

• De eerste term Cube, plus drievoudig het vierkant van de eerste termijn met de tweede.
• Plus drievoudig de eerste termijn, door de tweede kwadraat.
• Plus de kubus van de tweede termijn.

(A + B)³ = (a + b) _* (A + B)²

(A + B)³ = (a + b) _* (naar² + 2AB + B²))

(A + B)³ = A³ + 2e²B + AB² + ba² + 2AB² + B³

(A + B)³ = a³ + 3e²B + 3AB² + B³.

voorbeeld 1

(A + 3)³ = A³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = A³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = A³ + 9 a² + 27a + 27.

B. Voor de binomiale naar de kubus van een aftrekking:

• De kubus van de eerste termijn, behalve het drievoudige van het vierkant van de eerste termijn door de tweede.
• Plus drievoudig de eerste termijn, door de tweede kwadraat.
• Minder de kubus van de tweede termijn.

(A - b)³ = (a - b) _* (A - b)²

(A - b)³ = (a - b) _* (naar² - 2AB + B²))

(A - b)³ = A³ - 2e²B + AB² - ba² + 2AB² - B³

(A - b)³ = naar³ - 3e²B + 3AB² - B³.

Voorbeeld 2

(B - 5)³ = B³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = B³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Kan u van dienst zijn: niet -groepen gegevens: voorbeelden en oefening opgelost

(B - 5)³ = B³ - 15B² +75B - 125.

Trinomiale kubus

Het ontwikkelt het vermenigvuldigen met zijn vierkant. Het is een zeer uitgebreid opmerkelijk product omdat er 3 termen naar de kubus zijn verhoogd, plus de drievoudige van elke vierkante termijn, vermenigvuldigd door elk van de voorwaarden, plus zes keer het product van de drie termen. In een betere vorm gezien:

(A + B + C)³ = (A + b + c) _* (A + B + C)²

(A + B + C)³ = (A + b + c) _* (naar² + B² + C² + 2ab + 2ac + 2bc)

(A + B + C)³ = A³ + B³ + C³ + 3e²B + 3AB² + 3e²C + 3AC² + 3B²C + 3BC² + 6ABC.

voorbeeld 1

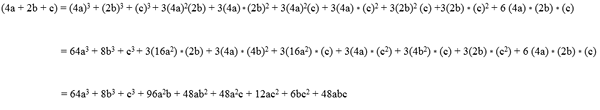
Opgeloste oefeningen van opmerkelijke producten

Oefening 1

Ontwikkel de volgende binomiale naar de kubus: (4x - 6)³.

Oplossing

Herinnerend dat een binomiale naar de kubus gelijk is aan de eerste term die aan de kubus is verhoogd, behalve de drievoudige van het vierkant van de eerste termijn door de tweede; Plus drievoudig de eerste termijn, door de tweede kwadraat, behalve de kubus van de tweede termijn.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288X² + 432x - 36.

Oefening 2

Ontwikkel de volgende binomiale: (x + 3) (x + 8).

Oplossing

Je hebt een binomiale waar er een gemeenschappelijke term is, die X is en de tweede term is positief. Om het te ontwikkelen, hoeft alleen de gemeenschappelijke term te worden verhoogd, plus de som van de termen die niet gebruikelijk zijn (3 en 8) en vermenigvuldig ze vervolgens met de gemeenschappelijke term, plus de som van de vermenigvuldiging van de termen die niet gebruikelijk zijn.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Referenties

1. Engel, een. R. (2007). Elementaire algebra. Pearson Education,.
2. Arthur Goodman, L. H. ( 1996). Algebra en trigonometrie met analytische geometrie. Pearson Education.
3. Das, s. (S.F.)). Wiskunde plus 8. Verenigd Koninkrijk: Sagar Ratna.
4. Jerome E. Kaufmann, K. L. (2011). Elementaire en tussenliggende algebra: een gecombineerde aanpak. Florida: Cengage Learning.
5. Pérez, c. D. (2010). Pearson Education.