Pentagonale prisma -kenmerken, delen, hoekpunten, randen, volume

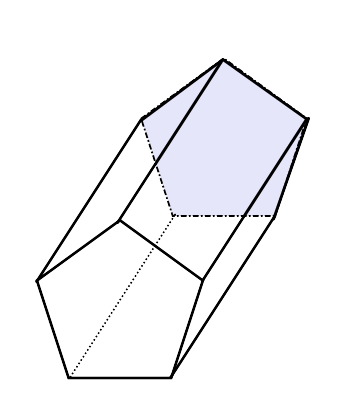
A Pentagonal Prism Het is een drie -dimensionale geometrische figuur wiens bases, identiek, een Pentagon -vorm hebben en ook in totaal 5 -sides heeft in de vorm van parallellogram.

Als de gezichten rechthoekig zijn, wordt gezegd dat het een Rechte Pentagonal Prism, Terwijl als de randen geneigd zijn naar de bases, dan een schuin Pentagonal Prism. In de volgende afbeelding is er een voorbeeld van elk.

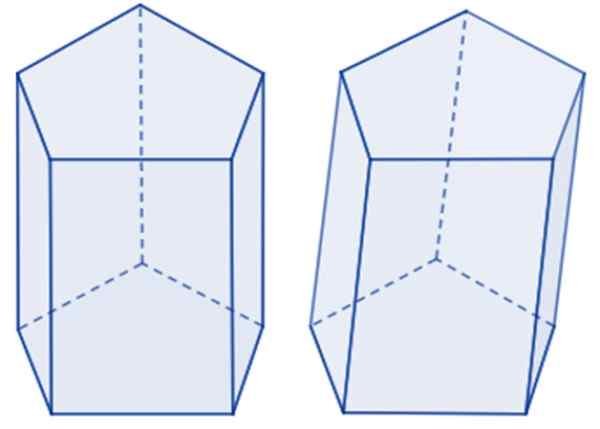Pentagonaal prisma links en schuin rechts. Bron: Wikimedia Commons.

De basis Pentagon kan regelmatig zijn als de vijf kanten dezelfde maatregel hebben, evenals interne hoeken, anders is het een onregelmatig Pentagon. Als de prisma -basis regelmatig is, gaat het erom Regelmatig Pentagonal Prism. Anders is een prisma onregelmatig pentagonaal.

Onregelmatige basistagonale prisma's die worden gebruikt in de moderne constructie. Bron: Wallpaper Flare.

Pentagonal prisma is een harmonieuze structuur die wordt gebruikt bij de architectuur en het ontwerp van objecten, zoals het moderne gebouw dat in de bovenste figuur wordt getoond. De vormige ramen van het onregelmatige Pentagon vormen de basis van de prisma's.

[TOC]

Pentagonale prisma -kenmerken

-Het is een drie -dimensionale geometrische figuur, de oppervlakken waaruit het samenstelt, bevatten een bepaald volume.

-Hun bases zijn pentagons en hun zijgezichten kunnen rechthoeken of parallellogrammen zijn.

-Het heeft hoekpunten -de hoeken van de prisma -en randen -bordes of kusten-.

-Als de randen die de basen verenigen loodrecht op hen staan, is het prisma recht en als ze geneigd zijn, is het prisma schuin.

-Wanneer de basis een Pentagon is waarvan de interne hoeken minder zijn dan 180º, is het prisma convex, Maar als een of meer interne hoeken groter zijn dan 180º, is het een prisma concaaf.

Pentagonale prisma -elementen

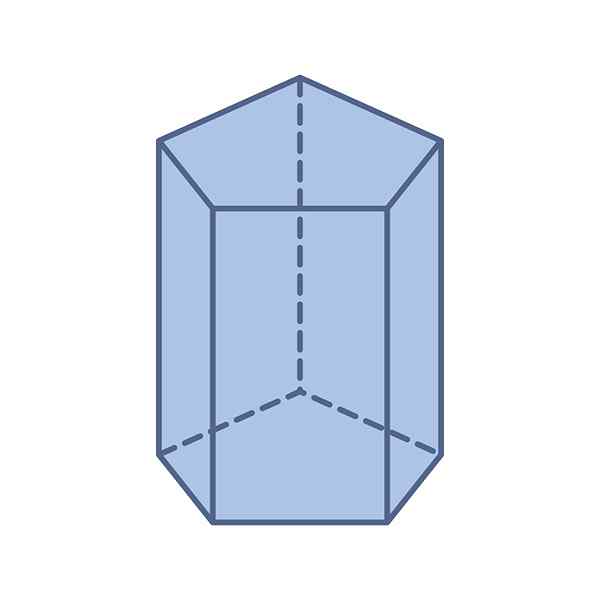
-Honken: Het heeft twee Pentagonal en congruente bases -hun metingen zijn hetzelfde -hetzij regelmatig of onregelmatig.

Kan u van dienst zijn: algemene formule: kwadratische vergelijkingen, voorbeelden, oefeningen

-Gezichten: Een Pentagonal Prism heeft in totaal 7 gezichten: de twee Pentagonal Bases en de vijf parallellogrammen die de zijkanten vormen.

-Rand: segment dat samenkomt.

-Hoogte: Afstand tussen de gezichten. Als het prisma recht is, valt deze afstand samen met de grootte van de rand.

-Hoekpunt: gemeenschappelijk punt tussen een basis en twee zijzijden.

De onderste figuur toont een regulier base pentagonaal prisma, waarin de segmenten die de basis vormen gelijke maatregel, genoemd, genoemd naar.

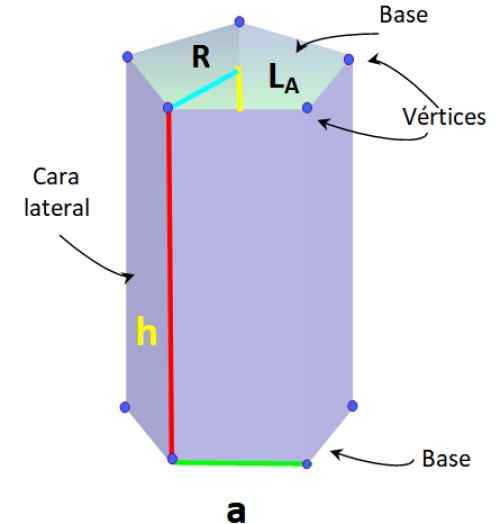 Regelmatige vijfhoekige prisma -elementen. Bron: f. Zapata.

Dit type prisma heeft ook de volgende elementen, typerend voor de reguliere Pentagon:

-Radio R: Afstand tussen het centrum van het Pentagon en een van de hoekpunten.

-Apothem l_NAAR: Segment dat zich bij het midden voegt met het middelpunt van een van de zijden van het Pentagon.

Hoeveel hoekpunten heeft een vijfhoekig prisma?

In een Pentagon zijn er 5 hoekpunten en omdat het vijfhoekige prisma twee pentagons als basen heeft, heeft dit lichaam in totaal 10 hoekpunten.

Hoeveel randen heeft een vijfhoekig prisma?

U kunt het aantal randen berekenen voor geometrische lichamen met vlakke gezichten, zoals prisma's, met behulp van de Euler Stelling Voor convexe polyhedros. Leonhard Euler (1707-1783) is een van de grootste wiskundigen en fysiek in de geschiedenis.

De stelling vestigt een relatie tussen het aantal gezichten, dat we C, de hoeveelheid hoekpunten V en de totale randen A als volgt zullen noemen:

C+v = a+2

Voor het Pentagonal Prism hebben we: C = 7 en V = 10. Opruimen van het aantal randen:

Het kan u van dienst zijn: bijjectieve functie: wat is het, hoe wordt het gedaan, voorbeelden, oefeningen

A = C+V-2

Waarden vervangen:

A = 7 + 10 - 2 = 15

Een vijfhoekig prisma heeft 15 randen.

Hoe u het volume van een vijfhoekige prisma kunt krijgen?

Het volume van het Pentagonal Prism meet de ruimte die wordt vergrendeld door de zijkanten en de bases. Het is een positief bedrag dat wordt berekend door de volgende eigenschap:

Elk vlak dat tot prisma loodrecht op zijn randen snijdt, genereert een kruising op dezelfde manier als de basis, dat wil zeggen een Pentagon van dezelfde afmetingen.

Daarom is het volume van het vijfhoekige prisma het product van het basisgebied en de hoogte van het prisma.

Zijn NAAR_B het vijfhoekige basisgebied en H De hoogte van het prisma, dan het volume V is:

V = a_B X H

Deze formule is algemeen, is geldig voor elk prisma, regelmatig of onregelmatig, recht of schuin.

Het volume van een prisma komt altijd in eenheden van lengte hoog voor de kubus. Als de lengte van de zijkanten en de hoogte van het prisma in meters worden gegeven, dan wordt het volume uitgedrukt in m³, dat "kubieke meter" wordt gelezen. Andere eenheden zijn CM³, km³, inches³ en meer.

- Regelmatig Pentagonal Prism Volume

In het Pentagonal Prism Regelmatig zijn de bases reguliere pentagons, wat betekent dat de zij- en interne hoeken hetzelfde zijn. Gezien de symmetrie van het lichaam, het Pentagon -gebied en daarom wordt het volume op verschillende manieren gemakkelijk berekend:

De hoogte en meting van de zijkant kennen

Zijn naar De maat van de vijfhoekige basiszijde. In dat geval wordt het gebied berekend door:

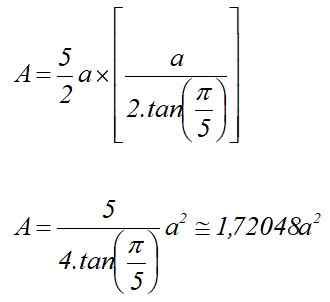
Daarom is het volume van het reguliere pentagonale prisma van hoogte H H:

Kan u van dienst zijn: denkbeeldige getallen: eigenschappen, toepassingen, voorbeelden

V = 1.72048 A²⋅ h

De hoogte en de maat van de radio kennen

Wanneer de Radio R Van de Pentagonal -basis kan deze andere vergelijking worden gebruikt voor het basisgebied:

A = (5/2) r²⋅ Sen 72º

Op deze manier wordt het volume van het vijfhoekige prisma gegeven door:

V = (5/2) r² ⋅ H ⋅ Sen 72º

Waar H Het is de hoogte van het prisma

De hoogte kennen, maat voor apotheme en perimeterwaarde

Het pentagonale basisgebied kan worden berekend als de perimeter P bekend is, wat gewoon de som van de zijkanten is, evenals de maat van de apothem l l l l l_NAAR:

A = P. L_NAAR / 2

Deze uitdrukking vermenigvuldigen met de hoogte van hoogte H, We hebben het volume van het prisma:

V = P. L_NAAR .H / 2

- Onregelmatig pentagonaal prisma -volume

De in het begin gegeven formule is zelfs geldig wanneer de basis van het prisma een onregelmatige Pentagon is:

V = a_B X H

Om het basisgebied te berekenen, worden verschillende methoden bijvoorbeeld gebruikt:

-Triangulatiemethode, die bestaat uit het verdelen van het Pentagon in driehoeken en vierhuizen, waarvan de respectieve gebieden gemakkelijk kunnen worden berekend. Het Pentagon -gebied zal de som zijn van de gebieden van deze eenvoudigere figuren.

-Gauss Determinants -methode, waarvoor u de hoekpunten van de figuur moet kennen.

Zodra de waarde van het gebied is bepaald, wordt deze vermenigvuldigd met de hoogte van het prisma om het volume te verkrijgen.

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Math Open Referentie. Polygoongebied. Hersteld van: Mathpenref.com.
3. Universe -formules. Euler -stelling voor polyhedros. Hersteld van: UniversOFormulas.com.
4. Universe -formules. Gebied van een gewone Pentagon. Hersteld van: UniversOFormulas.com.
5. Wikipedia. Prisma. Hersteld van: is.Wikipedia.com.
6. Wikipedia. Pentagonal Prism. Hersteld van: is.Wikipedia.com.