Manometrische drukverklaring, formules, vergelijkingen, voorbeelden

De buikdruk P_M Het is er een die wordt gemeten in relatie tot een referentiedruk, die in de meeste gevallen wordt gekozen als de atmosferische druk p p_Geldautomaat op zeeniveau. Het is dan een Relatieve druk, een andere term waarvoor het ook bekend is.

De andere manier waarop de druk meestal wordt gemeten, is het vergelijken met de absolute leegte, waarvan de druk altijd nul is. In dit geval is er sprake van de absolute druk, waaraan we zullen aangeven hoe P_naar.

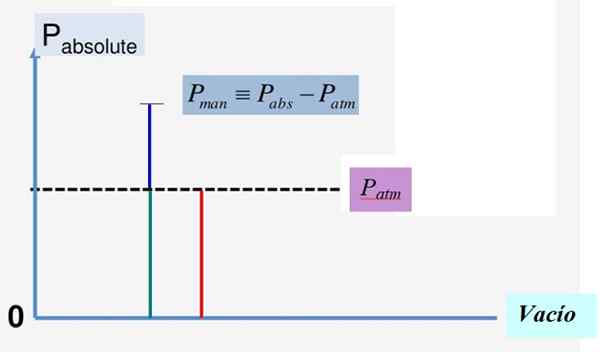
Figuur 1. Absolute druk en manometrische druk. Bron: f. Zapata.

De wiskundige relatie tussen deze drie hoeveelheden is:

P_naar = P_Geldautomaat + P_M

Daarom:

P_M = P_naar - P_Geldautomaat

Figuur 1 illustreert deze relatie handig. Omdat de vacuümdruk 0 is, is de absolute druk altijd positief en hetzelfde geldt voor atmosferische druk p p_Geldautomaat.

Manometrische druk wordt meestal gebruikt om drukken boven de atmosferische druk aan te duiden, zoals die van de banden of die op de bodem van de zee of een zwembad, dat wordt uitgeoefend door het gewicht van de waterkolom. In deze gevallen p_M > 0, sinds P_naar > P_Geldautomaat.

Er zijn echter absolute drukken onder p_Geldautomaat. In deze gevallen p_M < 0 y recibe el nombre de vacuümdruk En het moet niet worden verward met de druk van het reeds beschreven vacuüm, wat de afwezigheid is van deeltjes die in staat zijn om druk uit te oefenen.

[TOC]

Formules en vergelijkingen

De druk in een vloeistof -vloeistof of gas -is een van de belangrijkste variabelen in zijn studie. In een stationaire vloeistof is de druk op alle punten hetzelfde op dezelfde diepte, ongeacht de oriëntatie, terwijl de beweging van vloeistoffen in de leidingen wordt veroorzaakt door drukveranderingen.

De gemiddelde druk wordt gedefinieerd als het quotiënt tussen de kracht loodrecht op een oppervlak F_⊥ en het gebied van genoemde oppervlak A, dat wiskundig als volgt wordt uitgedrukt:

P = f_⊥ /NAAR

De druk is een scalaire hoeveelheid, waarvan de afmetingen van kracht zijn per eenheid van het gebied. De eenheden van uw maatregel in het International Units System (SI) zijn Newton/M², Pascal genoemd en afgekort als PA, ter ere van Blaise Pascal (1623-1662).

Veelvouden zoals kilo (10³) En mega (10⁶) Ze worden vaak gebruikt, omdat de atmosferische druk meestal in het bereik van 90 ligt.000 - 102.000 PA, die gelijk is aan: 90 - 102 kPa. De druk van de volgorde van de Mega Pascals is niet zeldzaam, dus het is belangrijk om vertrouwd te raken met de voorvoegsels.

In Anglo -Saxon -eenheden wordt de druk gemeten in ponden/voet², Het algemene ding moet echter worden gedaan in ponden/inch² of psi (Pond-force per vierkante inch)).

Kan u van dienst zijn: Warmtoverdracht: wetten, transmissievormen, voorbeelden

Variatie van druk met diepte

Hoe meer we onszelf onderdompelen in het water van een zwembad of in de zee, hoe meer druk we ervaren. Integendeel, toenemende hoogte, neemt de atmosferische druk af.

De gemiddelde atmosferische druk op zeeniveau is vastgesteld in 101300 PA of 101.3 kPa, terwijl in de Mariana -put in de westelijke Stille Oceaan - de grootste diepte die bekend is - het is ongeveer 1000 keer hoger en aan de top van Everest is slechts 34 kPa.

Het is duidelijk dat druk en diepte (of hoogte) gerelateerd zijn. Om te weten in het geval van een rustvloeistof (statische balans) wordt het beschouwd als een vloeistofgedeelte met schijfvormige vloeistof, beperkt in een container (zie figuur 2). De schijf heeft een dwarsdoorsnede NAAR, gewicht DW en lengte Dy.

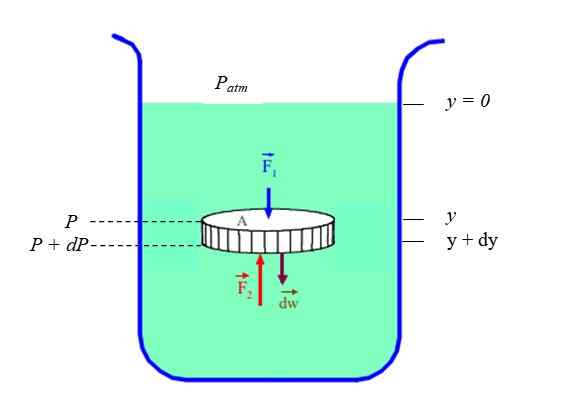Figuur 2. Differentiaal element van statische evenwichtsvloeistof. Bron: Fanny Zapata.

We zullen bellen P bij de druk die diepgaand bestaat "En" En P + DP bij de druk die diepgaand bestaat (en + dy)). Aangezien de dichtheid ρ van de vloeistof de reden is tussen zijn massa DM en het volume Dv, Je moet:

ρ = DM/ DV ⇒ DM = ρ.Dv

Daarom het gewicht DW van het element is:

DW = G. Dm = ρ.G.Dv

En nu is de tweede wet van Newton van toepassing:

Σ f_En = F₂ - F₁ - DW = 0

(P + DP).A - P.NAAR - ρ.G.Dv = 0

(P + DP).A - P.NAAR - ρ.G. NAAR. DY = 0

Dp = ρ.G.Dy

Differentiaalvergelijkingsoplossing 

Beide kanten integreren en die dichtheid overwegen ρ, evenals zwaartekracht G Ze zijn constant, er is de gezochte uitdrukking:

P₂ - P₁ = ΔP = ρ.G.(En₂ - En₁))

Δp = ρ.G. ΔEn

Als het in de vorige uitdrukking wordt gekozen P₁ zoals atmosferische druk en En₁ Zoals het oppervlak van de vloeistof dan En₂ Het bevindt zich op een diepte H En Δp = p₂ - P_Geldautomaat Het is de manometrische druk, afhankelijk van de diepte:

P_M = ρ.G.H

Als u de absolute drukwaarde nodig hebt, wordt de atmosferische druk eenvoudig toegevoegd aan het vorige resultaat.

Voorbeelden

Voor manometrische drukmaat wordt een apparaat gebruikt druk meter, die over het algemeen drukverschillen bieden. Uiteindelijk zal het werkingsprincipe van een U - -Shared -drukmanometer worden beschreven, maar laten we nu enkele belangrijke voorbeelden en gevolgen zien van de eerder afgetrokken vergelijking.

Het Pascal -principe

De vergelijking ΔP = ρ.G.(En₂ - En₁)) Het kan worden geschreven als  P = PO + ρ.G.H, waar P is de druk op diepte H, terwijl P_of Het is meestal de druk op het vloeistofoppervlak P_Geldautomaat.

Het is duidelijk dat elke keer dat je toeneemt Po, verhoogt P in dezelfde hoeveelheid, zolang het een vloeistof is waarvan de dichtheid constant is. Het is precies wat er moest overwegen ρ constant en plaats het buiten de integraal opgelost in de vorige sectie.

Kan u van dienst zijn: eenvoudige harmonische beweging

Het Pascal -principe stelt dat elke toename van de druk van een vloeistof beperkt in evenwicht, wordt overgedragen zonder enige variatie naar alle punten van genoemde vloeistof. Door deze eigenschap is het mogelijk om kracht te vermenigvuldigen F₁ toegepast op het kleine links van links, en verkrijgen F₂ aan de rechterkant.

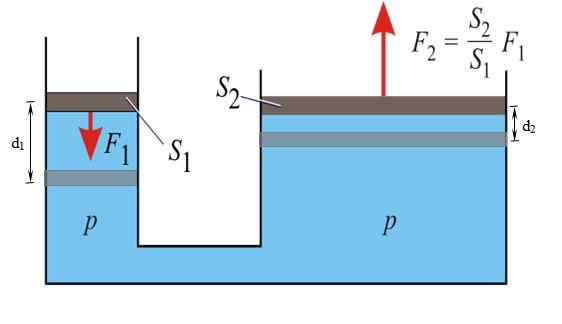figuur 3. In de hydraulische pers wordt het Pascal -principe toegepast. Bron: Wikimedia Commons.

Automobile remmen werken onder dit principe: een relatief kleine kracht wordt uitgeoefend op het pedaal, dat een belangrijke kracht wordt op de remcilinder op elk wiel, dankzij de vloeistof die in het systeem wordt gebruikt.

Stevin's hydrostatische paradox

De hydrostatische paradox stelt dat de kracht als gevolg van de druk van een vloeistof aan de onderkant van een container gelijk kan zijn, groter of minder dan het gewicht van de vloeistof zelf. Maar bij het plaatsen van de container op de schaal, registreert deze normaal gesproken het gewicht van de vloeistof (plus die van de container natuurlijk). Hoe u deze paradox uitlegt?

We beginnen met het feit dat de druk aan de onderkant van de container uitsluitend afhankelijk is van de diepte en onafhankelijk is van de vorm, zoals afgeleid in de voorgaande sectie.

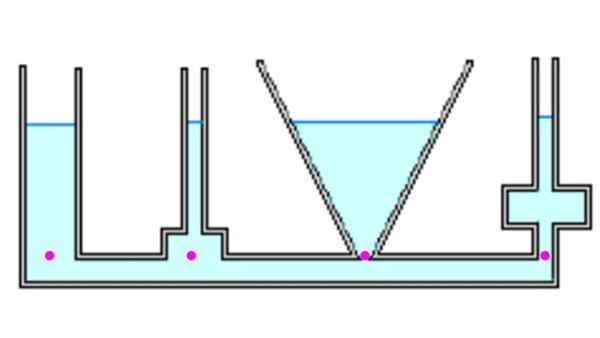Figuur 4. De vloeistof bereikt dezelfde hoogte in alle containers en de druk op de achtergrond is hetzelfde. Bron: f. Zapata.

Laten we eens kijken naar enkele verschillende containers. Wanneer ze worden gecommuniceerd, wanneer ze gevuld zijn met vloeistof, bereikt iedereen dezelfde hoogte H. De prominente punten zijn onder dezelfde druk, omdat ze op dezelfde diepte zijn. De kracht als gevolg van de druk op elk punt kan echter verschillen van het gewicht (zie voorbeeld 1 hieronder).

Opdrachten

Oefening 1

Vergelijk de kracht die wordt uitgeoefend door de druk op de bodem van elk van de containers met het gewicht van de vloeistof en leg uit waarom van de verschillen, als er een.

Container 1 

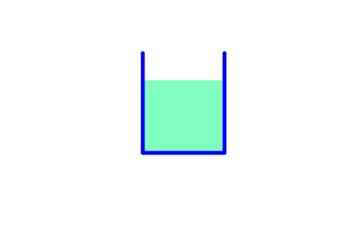Figuur 5. De druk op de achtergrond is in grootte hetzelfde als het gewicht van de vloeistof. Bron: Fanny Zapata.

In deze container is het basisgebied daarom een:

Vloeistofgewicht: mg = ρ.V.G = ρ . NAAR .H . G

Druk op de bodem: ρ. G. H

Kracht door druk: f = p.A = ρ. G. H. NAAR

Het gewicht en de kracht als gevolg van de druk zijn gelijk.

Container 2 

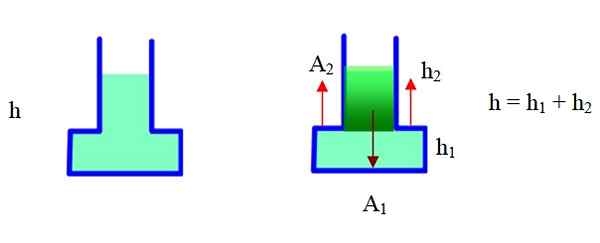Figuur 6. De kracht als gevolg van de druk in deze container is groter dan het gewicht. Bron: f. Zapata.

De container heeft een smal deel en een breed deel. In het juiste schema is het in twee delen verdeeld en zal de geometrie gebruiken om het totale volume te vinden. Het gebied a₂ is extern voor de container, h₂ Het is de hoogte van het smalle deel, h₁ Het is de hoogte van het brede deel (basis).

Kan u van dienst zijn: Pleiaden: geschiedenis, oorsprong en compositie

Het volledige volume is het volume van de basis + het volume van het smalle deel. Met deze gegevens heeft u:

Vloeistofgewicht: m . G = ρ . G. V = ρ . G. [NAAR₁ .H₁+ (NAAR₁ -NAAR₂)) .H₂] =

= ρ . G (a₁.Ha₂H₂) = ρ . G . NAAR₁.H - ρ . G . NAAR._. H₂ (Gebruik van h = H₁ +H₂))

Druk op de onderkant: p = ρ. G. H

Kracht op de bodem vanwege druk: f = p. NAAR₁ = ρ. G. H. NAAR₁

Het vergelijken van het gewicht van de vloeistof met de kracht vanwege de druk wordt opgemerkt dat dit groter is dan het gewicht.

Wat er gebeurt, is dat de vloeistof ook de sterkte uitoefent van de stap van de stap in de container (zie de rode pijlen van de figuur) die zijn opgenomen in de vorige berekening. Deze tegenwerkkracht voor degenen die zijn uitgeoefend en het gewicht dat door de schaal is geregistreerd, is het resultaat hiervan. Volgens dit is de omvang van het gewicht:

W = kracht op de achtergrond - sterkte op het gespreide deel = ρ . G . NAAR₁.H - ρ . G . NAAR._. H₂

Oefening 2

De figuur toont een open buisdrukmeter. Het bestaat uit een U -buis, waarin een van de uiteinden in atmosferische druk is en de andere verbindt met S, het systeem waarvan de druk zal worden gemeten.

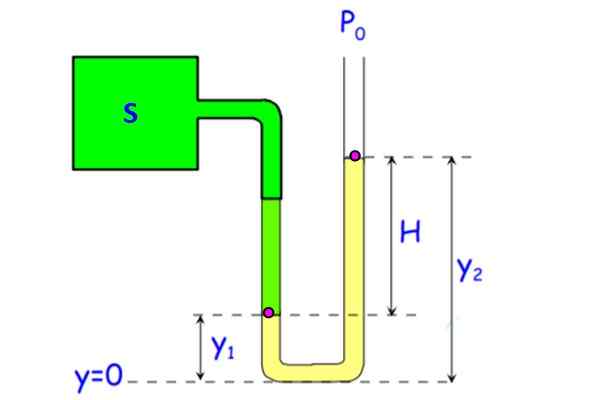Figuur 7. Open de buisdrukmeter. Bron: f. Zapata.

De vloeistof in de buis (in geel in de figuur) kan water zijn, hoewel kwik wordt gebruikt om de grootte van het apparaat te verminderen. (Een verschil van 1 atmosfeer of 101.3 kPa vereist een 10 waterkolom.3 meter, niets draagbaars).

Er wordt gevraagd om de manometrische druk te vinden P_M In het S -systeem, afhankelijk van de hoogte h van de vloeistofkolom.

Oplossing

De druk op de achtergrond voor beide takken van de buis is hetzelfde, omdat hij in dezelfde diepte zit. Laat P_NAAR De druk op punt A, gelegen in en₁ En P_B die van punt B die op de hoogte is en₂. Omdat punt B zich in het vloeistof- en luchtinterface bevindt, is de druk daar P_of. In deze tak van de drukmeter is de druk aan de onderkant:

PO + ρ.G.En₂

Van zijn kant is de druk aan de onderkant voor de tak van de linkerkant:

P + ρ.G.En₁

Waarbij p de absolute druk van het systeem is en ρ de dichtheid van de vloeistof is. Gelijk aan beide drukken:

PO + ρ.G.En₂ = P +ρ.G.En₁

Opruiming P:

P = PO + ρ.G.En₂ - ρ.G.En₁ = PO + ρ.g (en₂ - En₁) = PO + ρ.G. H

Daarom manometrische druk P_M Het wordt gegeven door P - P_of = ρ.G. H En om zijn waarde te hebben, is het voldoende om de hoogte te meten waarop de manometrische vloeistof stijgt en deze vermenigvuldigen met de waarde van G en vloeistofdichtheid.

Referenties

1. Cimbala, c. 2006. Mechanica van vloeistoffen, basisprincipes en toepassingen. MC. Graw Hill. 66-74.
2. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 4. Vloeistoffen en thermodynamica. Uitgegeven door Douglas Figueroa (USB). 3-25.
3. Mott, r. 2006. Vloeistofmechanica. 4e. Editie. Pearson Education. 53-70.
4. Shaugnessy, E. 2005. Inleiding tot vloeistofmechanica.Oxford Universiteit krant. 51 - 60.
5. Stylianos, v. 2016. Tot eenvoudige uitleg van de klassieke hydrostatische paradox. Hersteld van: Haimgaifman.Bestanden.WordPress.com