Cartesiaans vlak

Wat is het Cartesiaanse vliegtuig?

Hij Cartesiaans vlak Het bestaat uit een paar rechte lijnen loodrecht op elkaar en dat snijdt op een bepaald punt. Een van de lijnen is verticaal en de andere horizontaal en neemt naar het snijpunt als de oorsprong van het systeem.

Het doel is om gemakkelijk elk plat punt door een paar waarden te vinden: coördineren. Om dit te doen, op elk van de lijnen wordt een schaal met hele getallen geconstrueerd, de positieve worden in de ene richting geschreven en de negatieven in de andere, zoals weergegeven in de volgende figuur:

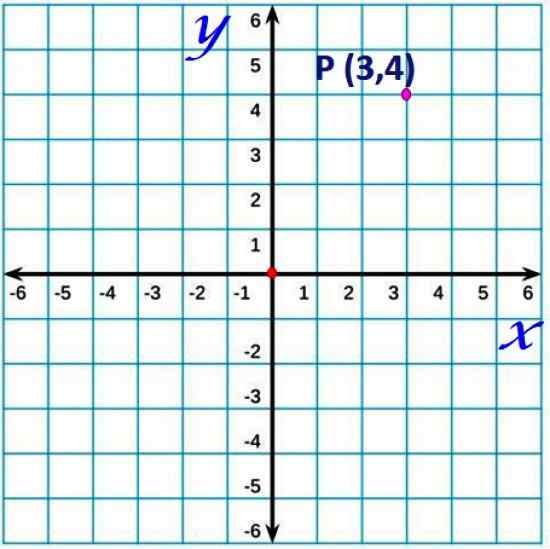
Figuur 1. Een punt in het Cartesiaanse vlak. Bron: f. Zapata.

Volgens de conventie wordt de horizontale as meestal X en verticale as genoemd als as en.

Een elk punt van het vlak heeft coördinaten die zijn gespecificeerd door een ordelijk paar (X, y). Bijvoorbeeld, het punt P van coördinaat (3,4), 3 eenheden rechts van de oorsprong en 4 eenheden omhoog, in de bovenste figuur. Het is vergelijkbaar met een kaart, die de breedtegraad en lengte van een bepaalde locatie aangeeft.

Omdat twee coördinaten nodig zijn, wordt gezegd dat het vlak twee -dimensionaal is, maar het concept wordt gemakkelijk uitgebreid tot drie dimensies, waardoor een meer coördinaatas wordt toegevoegd, die meestal wordt aangeduid als Z -as. In dit geval krijgen coördinaten vorm (X en Z).

Het Cartesiaanse vliegtuig ontvangt zijn naam aan de Franse wetenschapper René Descartes (1596-1650), die het in zijn werk formaliseerde Method Speech van 1637, hoewel er een geschiedenis is in de werken van Apollonius van Perga (262-190 AC), de wiskundige die de conische curven ontdekte: omtrek, ellips, gelijkenis en hyperbool.

Kan u van dienst zijn: Cubes Differention: Formules, Vergelijkingen, Voorbeelden, oefeningen

Kenmerken van het Cartesiaanse vlak

- Zoals hij X Axis Als de As y Ze strekken zich oneindig uit aan beide uiteinden en kruisen elkaar loodrecht op elkaar (onder een hoek van 90 graden). Deze functie wordt orthogonaliteit genoemd.

- Het punt waar beide assen elkaar kruisen, staat bekend als oorsprong of nul punt.

- Het coördinatensysteem verdeelt het vlak in vier gebieden die kwadranten worden genoemd.

- Locaties in het coördinaatvlak worden beschreven als geordende paren.

- Elk punt op het Cartesiaanse vlak wordt geassocieerd met een unieke X -coördinaat en een coördinaat en uniek.

Elementen van het Cartesiaanse vlak

De elementen van het Cartesiaanse vlak zijn de volgende:

-De numerieke lijnen of Coördinaatassen X en Y, Als het het vliegtuig is. De as En Ontvang de asnaam van de ordinaten, terwijl de as X Het is de as van abscis. Als het op ruimte aankomt, wordt de as toegevoegd Z, in staat om zowel hoogte als diepte te vertegenwoordigen.

-Hij oorsprong, dat is het punt van snijpunt van de assen.

-De kwadranten, die de gebieden zijn die de coördinaatassen op het vlak bepalen en in de tegenovergestelde richting van de klokken worden geteld, beginnend met het eerste kwadrant. Ze zijn als volgt gedefinieerd:

• Eerste kwadrant: assen X En En positief.
• Tweede kwadrant: overeenkomend met de negatieve X -as en de en positieve as.
• Derde kwadrant: het heeft beide negatieve assen.
• Vierde kwadrant: met de positieve X -as en de en negatieve as.

Over het algemeen worden kwadranten aangeduid met Romeinse nummers, zoals deze:

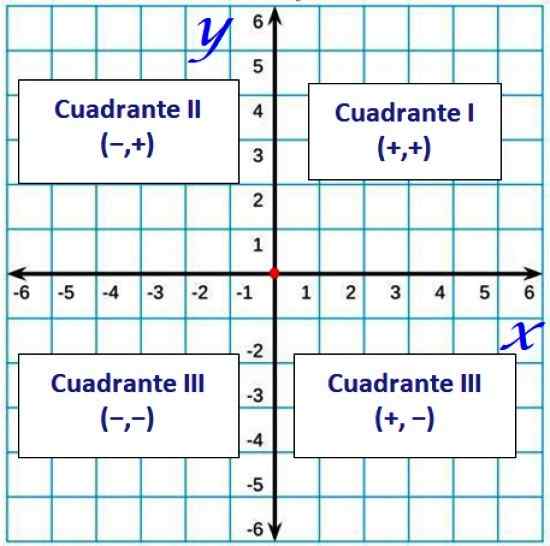Figuur 2. Cuadrants in het Cartesiaanse vlak. Bron: f. Zapata.

Bestelde paren en afstand tussen twee punten

De geordende paren zijn de coördinaten van elk punt, waarin de X -coördinaat altijd eerst wordt geplaatst, zoals in het voorbeeld van figuur 1. Coördinaten (3,4) van punt P geven dat aan X = 3 En y = 4.

In deze andere figuur hieronder behoort punt P tot het IV -kwadrant en heeft coördinaten (2; −1.5). Merk op dat door lijnen van de coördinaatassen naar het punt P een rechthoek vormt. Dit is de reden waarom Cartesiaanse coördinaten ook worden genoemd rechthoekige coördinaten.

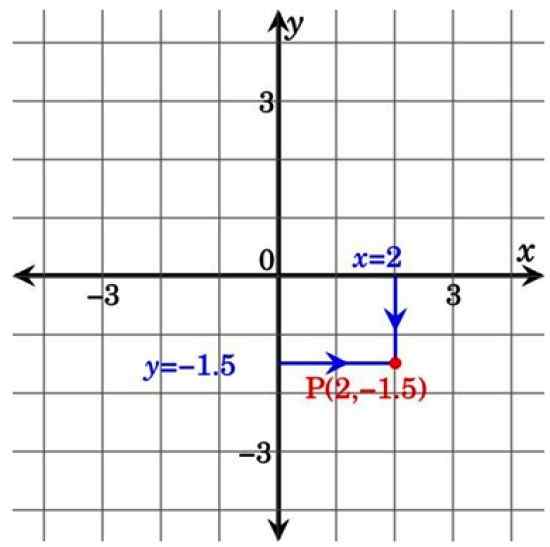figuur 3. Wijs op het Cartesiaanse vlak. Bron: Wikimedia Commons.

Cartesiaanse vlakke toepassingen

Het Cartesiaanse vlak heeft veel toepassingen op veel gebieden. Aanvankelijk introduceerde Descartes het in grafische curven van krommen in het vlak, daarom wordt het beschouwd als de vader van analytische geometrie.

Kan u van dienst zijn: Cruz -product

Het gebruik ervan strekt zich echter uit om alle soorten relaties en functies te verwerken, zoals:

-Volg het traject van een lichaam met parabolische, cirkelvormige of kromlijnige beweging in het algemeen.

-Bepaal grafisch de manier waarop twee variabelen gerelateerd zijn via een functie.

-Zoek punten op plat land om metingen op hen te vergemakkelijken.

Referenties

1. Wiskunde is leuk. Cartesiaanse coördinaten. Hersteld van: MathsisFun.com/data/cartesiaans-coördinaten.
2. Het Cartesiaanse vlak. Opgehaald van: DL.UNCW.Edu.