Pentadecágono -elementen, classificatie, kenmerken, oefening

A Pentadecantagon Het is een platte figuur gebouwd met vijftien rechte segmenten en dichtbij. Dit soort figuren worden genoemd veelhoek en ze worden genoemd volgens de hoeveelheid kanten die hebben.

De driehoek, met drie zijden en de vierhoek, van vier, zijn voorbeelden van zeer bekende polygonen, maar de polygonen hebben misschien meer kanten.

Figuur 1.  Regelmatig Pentagon met rode hoekpunten. Bron: Wikimedia Commons.

De basiselementen van de Pentadecágono zijn dezelfde als elke polygoon, ongeacht de hoeveelheid zijden die het bezit. Deze elementen zijn:

-Zijkanten, die de segmenten zijn die de Pentadecágono vormen voor een totaal van 15.

-Hoekpunten, ook 15, die de uiteinden van de aangrenzende kanten zijn.

-Interne hoeken, Degenen die worden gevormd in de Pentadecágono tussen twee aangrenzende kanten.

-Externe hoeken, gevormd tussen één kant en de verlenging van een van de opeenvolgende kanten.

-Diagonalen, De lijnsegmenten die zich aansluiten bij twee niet -adjacent hoekpunten.

[TOC]

Classificatie

Een pentadecágono kan zijn normaal of onregelmatig, Afhankelijk van de grootte van hun zijkanten en de maat voor zijn interne hoeken. Als u alle zijden en de gelijke interne hoeken hebt - QUILátero en Equiaggle - is het regelmatig, zoals weergegeven in figuur 1, anders is het onregelmatig.

Het kan ook worden geclassificeerd als convex of concaaf. Een concave Pentagon heeft een of meer interne hoeken groter dan 180º, terwijl één altijd convex interne hoeken heeft minder dan 180º. Het gewone Pentagon is convex.

Een andere classificatiecriteria wordt overwogen als de niet -opeenvolgende kanten - of hun uitbreidingen - zijn gesneden of niet. Wanneer ze niet worden gesneden, zoals in het geval van figuur 1, wordt gezegd dat het een eenvoudige pentadecágon is. En als ze worden gesneden, is het complex.

Het kan u van dienst zijn: analytische geometrie

Het gewone Pentagon

De reguliere Pentagon, wiens zijden en interne hoeken dezelfde maatregel hebben, is een figuur van grote symmetrie, omdat de volgende aanvullende elementen worden gedefinieerd voor die eerder beschreven:

-Centrum: Het punt dat equidista van de hoekpunten en de zijkanten.

-Radio: De afstand van het midden tot een van de reguliere hoekpunten van het Pentagon.

-Centrale hoek: Degene die zijn hoekpunt in het midden van de figuur heeft en zijn zijkanten passeren twee aangrenzende hoekpunten.

-Apothem, Het is het loodrechte segment dat bij het midden van de figuur het midden van één kant verbindt.

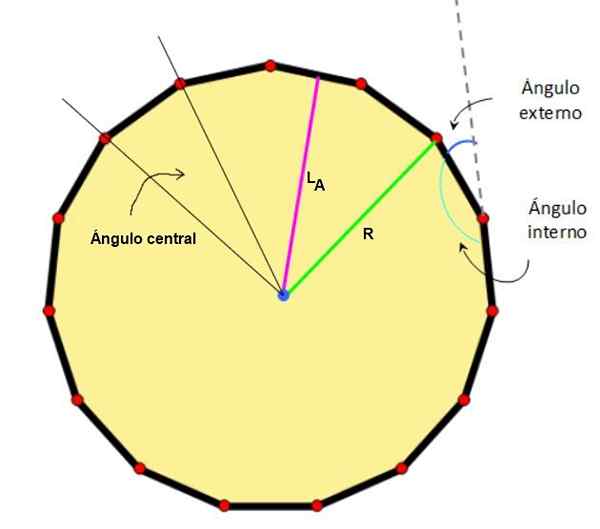Figuur 2. Midden, apothem, radio en opmerkelijke hoeken van een pentadecágono. Bron: Wikimedia Commons/F. Zapata.

- Kenmerken van het gewone Pentagon

Interne hoeken

De volgende formule wordt gebruikt om maat I te berekenen van de interne hoeken van elke gewone polygoon, waar N Het is het aantal zijden:

In deze formule, de maatregel die ik in graden komt, om het in radianen uit te drukken, wordt deze vermenigvuldigd met de π/180 -factor. Laten we eens kijken wat de maat is van de interne hoeken van de reguliere Pentagon, ter vervanging van n = 15:

I = [(15-2) × 180º]/15 = 156º

Gelijk aan 13π/15 radialen. Omdat de interne hoeken van het gewone Pentagon minder zijn dan 180º, is het een bolle polygoon.

Som van interne hoeken

Het is mogelijk om de som van de interne hoeken te berekenen door de volgende formule:

S = (N-2) x 180º

Zoals altijd vertegenwoordigt N het aantal kanten. Deze formule is geldig voor n = 3, 4, 5 .. .

N = 15 doen, krijgen we:

S = (15 - 2) x 180º = 2340º

Externe hoeken

Een interne hoek en een externe hoek zijn aanvullend, dat wil zeggen, de som is 180º, zoals opgemerkt in figuur 2. Daarom meet een externe hoek van de Pentadecágono:

Kan u van dienst zijn: geconjugeerd binomiaal: hoe het is opgelost, voorbeelden, oefeningen

180 º - 156º = 24º.

Perimeter en gebied

De perimeter is de maat van de polygooncontour en voegt gemakkelijk alle kanten toe. Ja naar Het is de lengte van de zijkant, het is voldoende om zich te vermenigvuldigen N, Het aantal kanten.

Voor een normale Pentagon van zij A is de omtrek P:

P = 15a

Als het een onregelmatige figuur is, waarbij de maat van de zijkanten verschilt, voegt de omtrek de lengte van al zijn zijden toe.

Wat het gebied betreft, we kunnen het op verschillende manieren berekenen. We hebben bijvoorbeeld de formule waarmee u deze kunt verkrijgen die de lengte A van zijn zijkanten kent:

Het uitvoeren van de aangegeven bewerkingen, het blijft ongeveer:

A = 17.6426⋅A²

Er is een andere optie, van toepassing op reguliere polygonen. Het gaat erom ze te verdelen in basis driehoeken gelijk aan de polygoon. De hoogte van de driehoek is de lengte van de apothem l_NAAR, hierboven gedefinieerd.

Het gebied van genoemde driehoek wordt berekend met de goed bekende formule: basis x hoogte /2. Op deze manier is het enkele driehoekige gebied:

Gebied = a. L_NAAR /2

Om de totale oppervlakte van de polygoon te hebben, is het voldoende om te vermenigvuldigen met het aantal zijden N, dat in dit geval 15 is:

A = 15⋅A⋅ L_NAAR /2

En omdat de omtrek van de figuur p = 15⋅A is, dan:

A = P⋅ L_NAAR /2

Diagonalen

De diagonalen zijn de segmenten die twee niet -opeenvolgende hoekpunten verenigen, zoals hierboven vermeld. Om te weten hoeveel diagonalen een gewone polygoon heeft N Kides, inclusief Pentadecágono, er is de volgende formule:

Waar D het aantal diagonalen is.

Nu vervangen we n = 15 om de totale diagonalen te verkrijgen:

Kan u van dienst zijn: reguliere polygonen: eigenschappen, elementen, hoeken, voorbeelden

D = [15 × (15-3)]/2 = 90 diagonalen.

Constructie met regel en kompas

Pentadecágono is gebouwd met regel en kompas dat begint bij een omtrek. De 360º moet worden verdeeld in 15 gelijke delen van elk 24º. Eerst worden de hulpconstructies aangegeven in de animatie uitgevoerd om een ​​hoek van 60º te verkrijgen, die op zijn beurt wordt verdeeld in 36º en 24º.

figuur 3. Constructie met heerschappij en kompas van een gewone Pentagon. Bron: Wikimedia Commons.

Oefening opgelost

Als de omtrek van een Pentadecágono geregistreerd in een cirkel van straal R 12,56 cm is. Berekenen:

a) de radio.

b) Uw gebied.

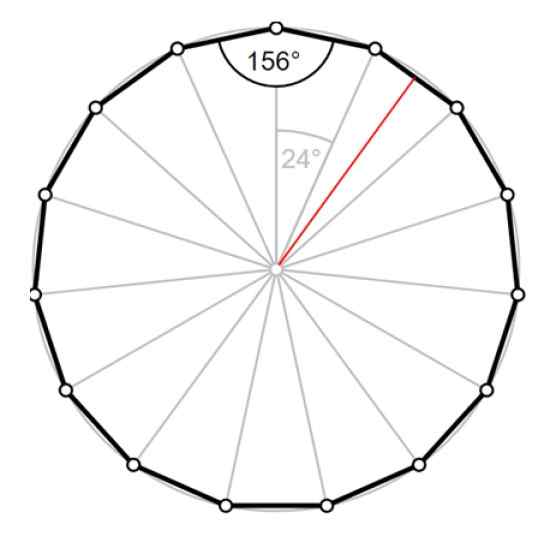Figuur 4. Pentadecágono: Centrale hoek, interne hoek en rood apothema. Bron: Wikimedia Commons/F. Zapata.

Oplossing voor

De perimeter is p = 15⋅a = 12.56 cm daarom de kant van Pentadecágono is 0.8373 cm. De radio We kunnen het berekenen met behulp van een van de driehoeken in figuur 4.

De apothem l_NAAR komt overeen met de hoogte van de driehoek, in rood getrokken, die de hoek van 24º in twee hoeken van elk 12º verdeelt elk.

Er zijn twee rechtse driehoeken met een interne hoek van elk 12º, en op een van hen kunnen we trigonometrie toepassen om de hypotenuse te vinden, die de lengte R van de straal is.

Op deze manier:

Sen 12º = (a /2) /r

R = (a /2) /sen 12º = (0.8373 cm / 2) / sen12º = 2.01 cm.

Oplossing B

We kunnen het Pentadecágono -gebied berekenen met behulp van de formule:

A = P⋅ L_NAAR /2

We kennen de perimeter P = 12 al.56 cm, en de lengte van de apothem wordt berekend door de raaklijn of de 12º cosinus:

Cos 12º = l_NAAR / R

L_NAAR = R. Cos 12 º = 2.01 cm. Cos 12 º = 1.97 cm

Vervangen:

A = 12.56 cm⋅ 1.97 cm /2 = 12.35 cm²

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Leer wiskunde. Geometrische figuren. Hersteld van: Rodrigoanchorena.Wixsite.com.
3. Sangaku -wiskunde. Elementen van een polygoon en zijn classificatie. Hersteld van: Sangakoo.com.
4. Wikipedia. Pentadecágono. Hersteld van: is.Wikipedia.borg.
5. Wolfram Math World. Pentadecagon. Hersteld van: Mathworld.Wolfraam.com.