Parallellepipedum

De parallellepipeds zijn zes -zijdige geometrische figuren, waar tegenstellingen parallel aan elkaar zijn. Voorbeeld: een baksteen, een schoenendoos, een emmer, enz.

Wat is een parallellepiped?

A parallellepipedum Het is een geometrisch lichaam gevormd door zes gezichten, wiens hoofdkenmerk is dat al zijn gezichten parallellogrammen zijn en ook de tegenovergestelde gezichten parallel aan elkaar zijn. Het is een veel voorkomende polyhedron in ons dagelijks leven, omdat we het in schoenendozen kunnen vinden, de vorm van een baksteen, de vorm van een magnetron, enz.

Als een polyhedron, bevat de parallellepiped een eindig volume en al zijn gezichten zijn plat. Het maakt deel uit van de groep prisma's, die die polyhedra zijn waarin alle hoekpunten zijn opgenomen in twee parallelle vlakken.

Elementen van de parallellepiped

Gezichten

Het zijn elk van de regio's gevormd door parallellogrammen die de parallellepiped beperken. Een parallellepiped heeft zes gezichten, waarbij elk gezicht vier aangrenzende gezichten heeft en een tegenovergestelde. Bovendien is elk gezicht parallel met zijn tegenovergestelde.

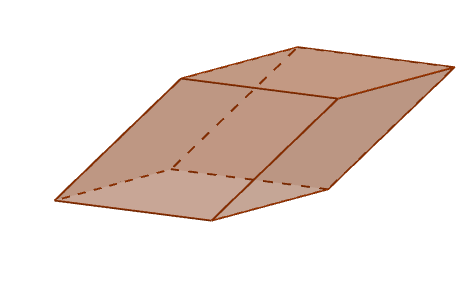Perspectief van een parallellepiped

Randen

Ze zijn de gemeenschappelijke kant van twee gezichten. In totaal heeft een parallellepiped twaalf randen.

Hoekpunt

Het is het gemeenschappelijke punt van drie gezichten die twee tot twee aangrenzen. Een parallellepiped heeft acht hoekpunten.

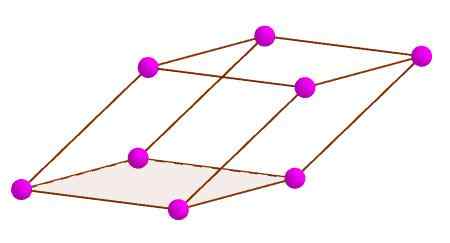Hoekpunten van een parallellepiped

Diagonaal

Gegeven twee gezichten van een parallellepiped tegenover elkaar, kunnen we een lijnsegment tekenen dat van het hoekpunt van het ene gezicht naar het tegenovergestelde hoekpunt van het andere gaat.

Dit segment staat bekend als de parallellepiped diagonaal. Elke parallellepiped heeft vier diagonalen.

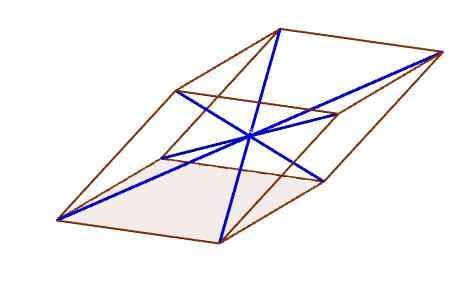Diagonalen van een parallellepiped

Centrum

Het is het punt waarop alle diagonalen kruisen.

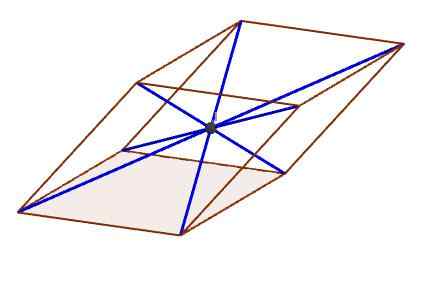Het punt in de figuur geeft het midden aan, waar alle diagonalen kruisen

Kenmerken van de parallellepiped

Zoals we al zeiden, heeft dit geometrische lichaam twaalf randen, zes gezichten en acht hoekpunten.

In een parallellepiped kunnen drie sets gevormd door vier randen worden geïdentificeerd, die parallel aan elkaar zijn. Bovendien voldoen de randen van deze sets ook aan de eigenschap van dezelfde lengte.

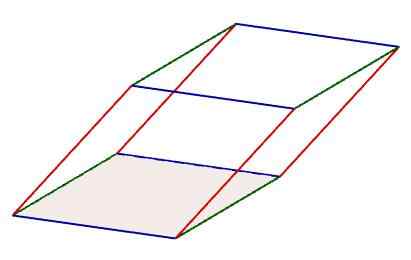Kenmerken van de parallellepiped

Een ander eigendom stelde.

Bovendien voldoen de parallellepipeds, zijnde convexe polyhedros, voldoen aan de stelling van Euler voor polyhedros, die ons een relatie geeft tussen het aantal gezichten, het aantal randen en het aantal hoekpunten. Deze relatie wordt gegeven in de vorm van de volgende vergelijking:

C + v = a + 2

Deze functie staat bekend als het kenmerk van Euler. Waarbij C het aantal gezichten is en het aantal hoekpunten en het aantal randen.

Soorten paralleepípedos

We kunnen de parallellepípedos classificeren op basis van hun gezichten, op de volgende typen:

Ortoedro

Zij zijn de parallellepípedos waar hun gezichten bestaan ​​uit zes rechthoeken. Elke rechthoek staat loodrecht op die waarmee hij rand deelt. Ze zijn de meest voorkomende in ons dagelijks leven, dit is de gebruikelijke vorm van schoenen en bakstenen dozen.

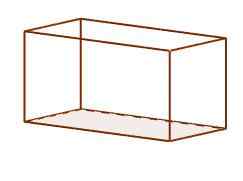Orthoedro parallelpiped

Gewone kubus of hexaedro

Dit is een bepaald geval van de vorige, waarbij elk van de gezichten een vierkant is.

Kan u van dienst zijn: ellipsGewone kubus of hexaedro

De kubus maakt ook deel uit van de geometrische lichamen die platonische vaste stoffen worden genoemd. Een platonische vaste stof is een convexe polyhedron, zodat zowel zijn gezichten als zijn interne hoeken gelijk zijn aan elkaar.

Romboedro

Het is een parallellepiped die een rhombus heeft. Deze rhombussen zijn allemaal gelijk aan elkaar, omdat ze randen delen.

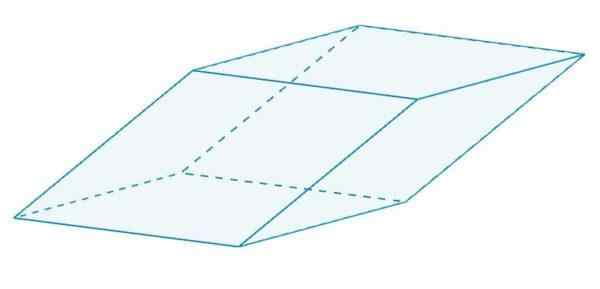Een romboor

Romboiedro

Zijn zes gezichten zijn rhomboid. Bedenk dat een rhomboid een vierzijdige polygoon is en vier hoeken die gelijk zijn aan twee tot twee. De rhomboids zijn de parallellogrammen die noch vierkant, noch rechthoeken, noch rhombuses zijn.

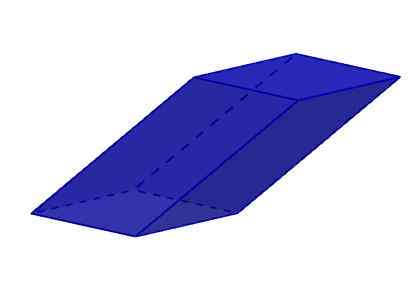Romboiedro

Aan de andere kant zijn de schuine parallellepipeds die waarin ten minste één hoogte niet overeenkomt met de rand. In deze classificatie kunnen we rhomboedros en rhomboiedros opnemen.

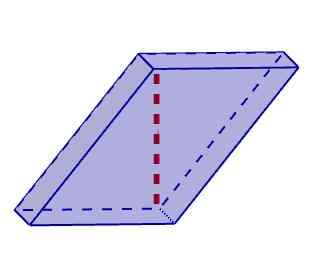Schuin parallelpiped

Diagonale berekening

Om de diagonaal van een orthoedro te berekenen, kunnen we de Pythagoras -stelling voor r gebruiken³.

Bedenk dat een orthoedro het kenmerk heeft dat elke partij loodrecht staat op de zijkanten die rand deelt. Uit dit feit kunnen we afleiden dat elke rand loodrecht is met die welke hoekpunt deelt.

Om de lengte van een diagonaal van een orthoedro te berekenen, gaan we als volgt verder:

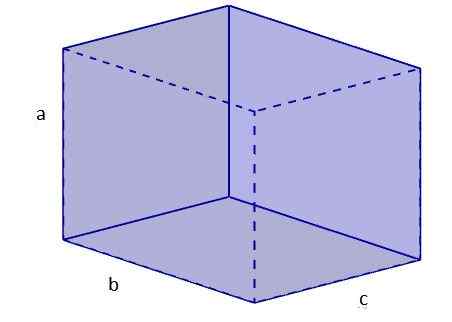
1. We berekenen de diagonaal van een van de gezichten, die we aan de basis zullen plaatsen. Hiervoor gebruiken we Pythagoras Stelling. Laten we die diagonale D noemen_B.

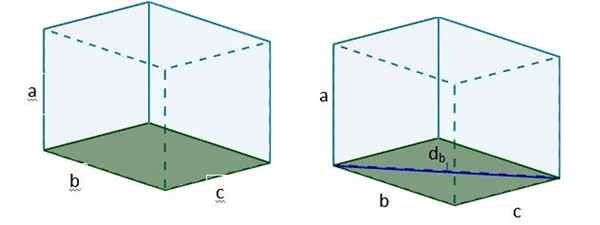
2. Dan met D_B We kunnen een nieuwe rechthoekige driehoek vormen, zodat de hypotenusa van deze driehoek de gevraagde diagonale D is.

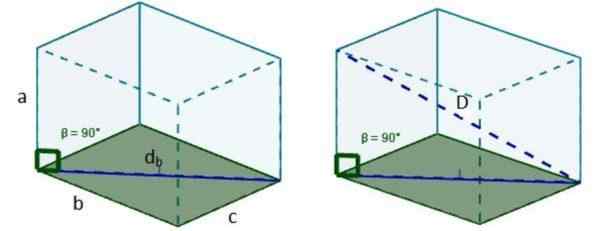
3. We gebruiken de stelling van Pythagoras opnieuw en we hebben dat de lengte van die diagonaal is:

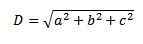
Een andere manier om diagonaal op een meer grafische manier te berekenen, is met de som van vrije vectoren.

Bedenk dat twee vrije vectoren A en B worden toegevoegd door de staart van vector B te plaatsen met de punt van de vector a.

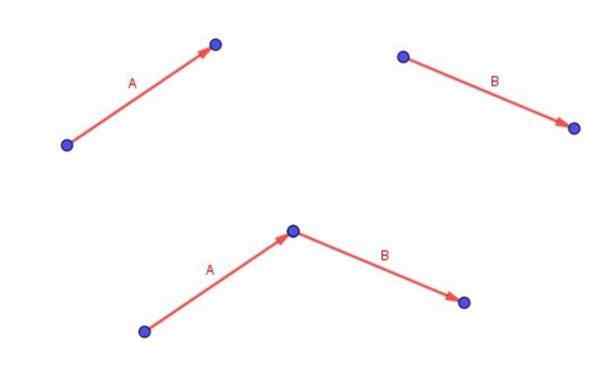
De vector (A + B) is degene die begint in de staart van A en eindigt op het puntje van B.

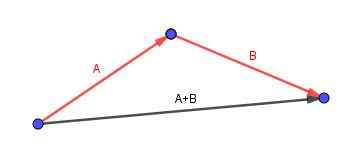
Overweeg een parallellepiped waarnaar we een diagonaal willen berekenen. We identificeren de randen met handige georiënteerde vectoren.

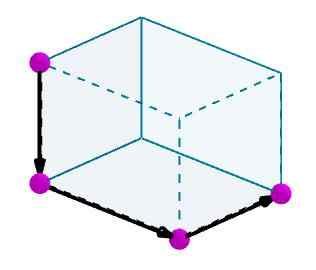
Vervolgens voegen we deze vectoren toe en de resulterende vector zal de diagonaal van de parallelpiped zijn.

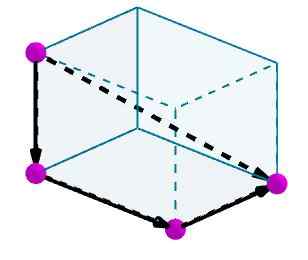
Gebied van een parallellepiped

Het gebied van een parallellepiped wordt gegeven door de som van elk van de delen van zijn gezichten.

Als we een van de zijkanten als basis bepalen,

NAAR_L + 2e_B = Totaal gebied

Waarheen_L Het is gelijk aan de som van de gebieden van alle kanten grenzend aan de basis, het zijgebied genoemd en aan_B Het is het basisgebied.

Afhankelijk van het type parallellepiped waarmee we werken, kunnen we de formule herschrijven.

Gebied van een orthoedro

Wordt gegeven door de formule

A = 2 (AB + BC + CA).

voorbeeld 1

Gegeven de volgende orthoedro, met zijkanten A = 6 cm, B = 8 cm en C = 10 cm, bereken het parallellepiped gebied en de lengte van de diagonaal.

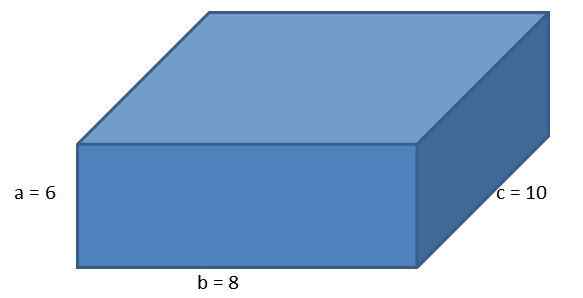
Met behulp van de formule voor het gebied van een orthoedro moeten we

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Merk op dat als een orthoedro de lengte van een van zijn vier diagonalen is, hetzelfde is.

Het kan u van dienst zijn: onbepaalde integrale: eigenschappen, toepassingen, berekening (voorbeelden)

Met behulp van de Pythagoras -stelling voor ruimte die we moeten

D = (6² + 8² + 10²))^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Kubusgebied

Omdat elke rand dezelfde lengte heeft, hebben we die a = b en a = c. Vervangen in de vorige formule die we hebben

A = 2 (aa + aa + aa) = 2 (3a²) = 6a²

A = 6A²

Voorbeeld 2

De doos van een spelconsole heeft de vorm van een kubus. Als we deze doos met geschenkpapier willen inpakken, hoeveel papier zou we dan besteden te weten dat de lengte van de randen van de kubus 45 cm is?

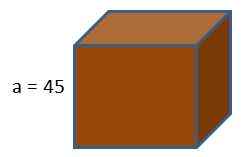
Met behulp van de formule van het kubusgebied krijgen we dat

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Gebied van een rhomboedro

Omdat al zijn gezichten hetzelfde zijn, is het voldoende om het gebied van een van hen te berekenen en het met zes te vermenigvuldigen.

We hebben dat het gebied van een rhombus kan worden berekend door de diagonalen met de volgende formule

NAAR_R = (DD)/2

Met behulp van deze formule volgt hieruit dat de totale oppervlakte van de rhomboedro is

NAAR_T = 6 (dd)/2 = 3DD.

Voorbeeld 3

De gezichten van de volgende rhomboedro worden gevormd door een rhombus waarvan de diagonaal d = 7 cm en d = 4 cm zijn. Uw gebied zal zijn

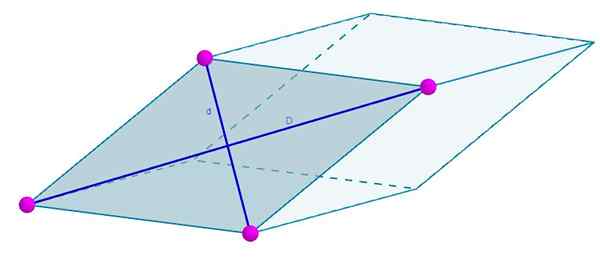
A = 3 (7 cm) (4 cm) = 84 cm².

Gebied van een rhomboiedro

Om het gebied van een rhomboiedro te berekenen, moeten we het gebied van de rhomboids berekenen die het samenstellen. Terwijl de parallellepipeds het eigendom vervullen dat de tegenoverliggende zijden hetzelfde gebied hebben, kunnen we de zijkanten in drie collega's associëren.

Op deze manier hebben we dat uw gebied zal zijn

NAAR_T = 2B₁H₁ + 2B₂H₂ + 2B₃H₃

Waar B_Je zijn de bases geassocieerd met de zijkanten en h_Je De relatieve hoogte die overeenkomt met genoemde bases.

Voorbeeld 4

Overweeg de volgende parallellepiped,

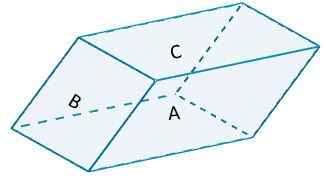
Waar zij A en zijde A '(hun tegenovergestelde zijde) gebaseerd zijn op B = 10 en per hoogte H = 6. Het gemarkeerde gebied zal een waarde hebben van

NAAR₁ = 2 (10) (6) = 120

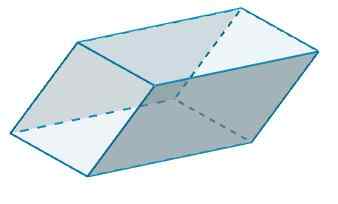
B en B 'hebben dan B = 4 en H = 6, dan

NAAR₂ = 2 (4) (6) = 48

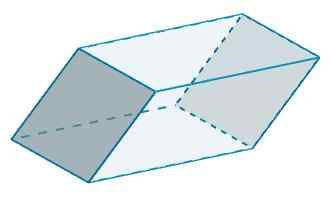
En C en C 'hebben ook B = 10 en H = 5

NAAR₃ = 2 (10) (5) = 100

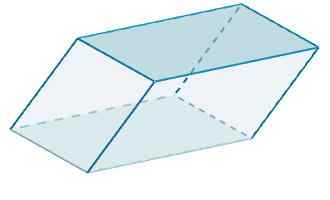
Eindelijk is het Rhomboiedro -gebied

A = 120 + 48 + 100 = 268.

Volume van een parallellepiped

De formule die ons het volume van een parallellepiped geeft, is het product van het gebied van een van zijn gezichten vanwege de hoogte die overeenkomt met dat gezicht.

V = a_CH_C

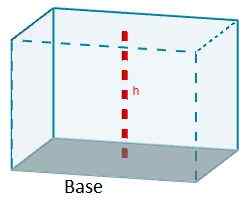
Afhankelijk van het type parallellepiped, kan deze formule worden vereenvoudigd.

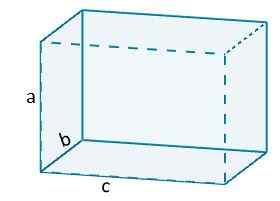
We hebben dus bijvoorbeeld dat het volume van een orthoedro zou worden gegeven door

V = ABC.

Waarbij a, b en c de lengte van de orthoedroranden vertegenwoordigen.

En in het specifieke geval van de kubus is

V = a³

voorbeeld 1

Er zijn drie verschillende modellen voor cookieboxen en je wilt.

De eerste is een kubus waarvan de rand een lengte van a = 10 cm heeft.

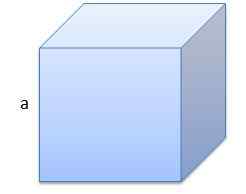
Het volume zal V = 1000 cm zijn³

De tweede is b = 17 cm, c = 5 cm, d = 9 cm.

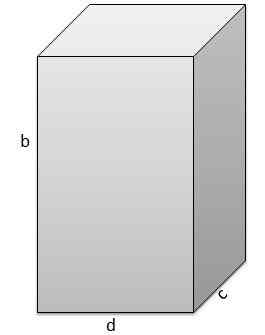
En daarom is het volume V = 765 cm³

En de derde heeft E = 9 cm, F = 9 cm en g = 13 cm.

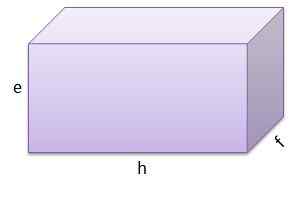
En het volume is V = 1053 cm³

Kan u van dienst zijn: soorten hoeken, kenmerken en voorbeelden

Daarom is de doos met het grootste volume de derde.

Een andere methode om het volume van een parallellepiped te verkrijgen, is om hun toevlucht te nemen tot vectoralgebra. In het bijzonder het drievoudige scalaire product.

Een van de geometrische interpretaties van het drievoudige scalaire product is dat van het volume van de parallellepiped, waarvan de randen drie vectoren zijn die hetzelfde hoekpunt delen als een startpunt.

Op deze manier, als we een parallellepiped hebben en we willen weten wat het volume ervan is, is het voldoende om het weer te geven in een coördinatensysteem in r³ samenvallen van een van zijn hoekpunten met de oorsprong.

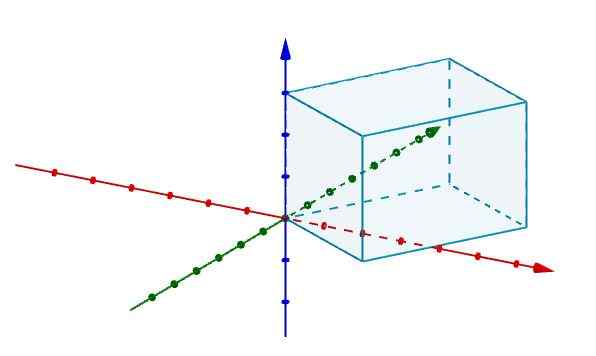
Vervolgens vertegenwoordigen we de randen die overeenkomen met de oorsprong met vectoren, zoals weergegeven in de figuur.

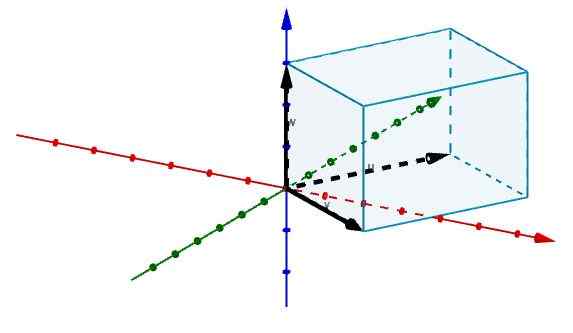
En op deze manier hebben we dat het aantal genoemde parallellepiped wordt gegeven door

V = | Axb ∙ C |

Of gelijkwaardig, het volume is de bepalende factor van de 3 × 3 -matrix, gevormd door de componenten van de randvectoren.

Voorbeeld 2

Door de volgende parallellepiped in r te vertegenwoordigen³ We kunnen zien dat de vectoren die het bepalen de volgende zijn

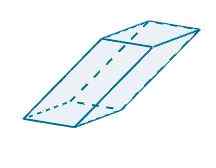
u = (-1, -3.0), v = (5, 0, 0) en w = (-0.25, -4, 4)

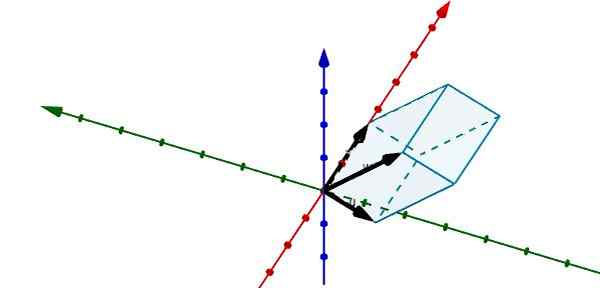
Met behulp van het drievoudige scalaire product dat we hebben

V = | (Uxv) ∙ w |

Uxv = (-1, -3.0) x (5, 0, 0) = (0.0, -15)

(Uxv) ∙ w = (0.0,- 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

Dit concludeert dat v = 60

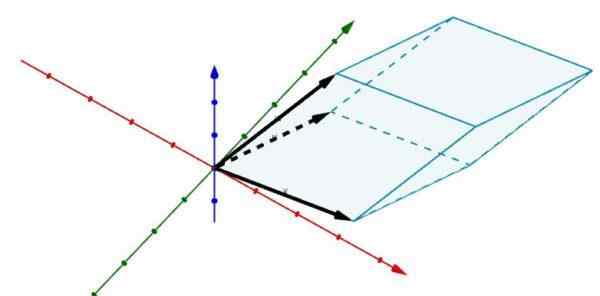
Beschouw nu de volgende parallellepiped in r³ wiens randen worden bepaald door de vectoren

A = (2, 5, 0), B = (6, 1, 0) en C = (3, 4, 4)

Het gebruik van determinanten geeft ons dat

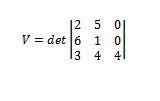
We hebben dus dat het volume van genoemde parallellepiped 112 is.

Beide zijn equivalente manieren om het volume te berekenen.

Perfect parallellepiped

Het staat bekend als Euler Brick (of Euler Block) tot een orthoedro die de eigenschap vervult dat zowel de lengte van de randen als de lengte van de diagonalen van elk van zijn gezichten hele getallen zijn.

Terwijl Euler niet de eerste wetenschapper was die de orthoeders bestudeerde die die eigendom ontmoeten, vond hij wel interessante resultaten over hen.

De kleinste Euler-baksteen werd ontdekt door Paul Halcke (1662-1731) en de lengte van de randen zijn a = 44, b = 117 en c = 240.

Een open probleem in getallen theorie is als volgt:

Zijn er perfecte orthoeder?

Op dit moment heeft deze vraag nog steeds geen antwoord, omdat het niet mogelijk is geweest om te bewijzen dat er geen lichamen zijn, maar er is niemand gevonden.

Wat tot nu toe is aangetoond, is dat het perfecte parallellepiped doet. De eerste die wordt ontdekt heeft als lengte van zijn randen de waarden 103, 106 en 271.

Referenties

1. Man, r. (1981). Onopgeloste problemen in getallentheorie. Springer.
2. Landaverde, f. D. (1997). Geometrie. Voortgang.
3. Leithold, l. (1992). De berekening met analytische geometrie. Harla, s.NAAR.
4. Rendon, een. (2004). Technische tekening: activiteiten notebook 3 2e baccalaureaat. Tebar.
5. Resnick, r., Halliday, D., & Krane, K. (2001). Vol -fysica. 1. Mexico: continentaal.