Besteld paar

Wat is een geordend paar?

Een geordend paar of duo Het is een set van twee elementen die zijn geschreven volgens de bestelling die door een bepaald criterium is vastgesteld. De criteria hebben gespecificeerd welke van de twee elementen het eerst verloopt en welke erna gaat.

Het geordende paar wordt aangeduid als (x, y), waarbij "x" het eerste element van het paar is en "y" het tweede is, ook wel genoemd Componenten. Over het algemeen (x, y) is het niet hetzelfde nette koppel (y, x). En naast de volgorde is een ander belangrijk kenmerk van de geordende paren gelijkheid: twee geordende paren (a, b) en (c, d) zijn alleen hetzelfde als a = c en b = d.

Figuur 1.- Dankzij de nette paren weet de puppy dat de botten op de locaties zijn begraven (3,1) en (-4,2), terwijl zijn huis zich bevindt (0.0). Bron: f. Zapata.

Voorbeelden van geordende paren zouden die zijn die zijn samengesteld uit leeftijd en het gewicht van een cursus wiskundestudenten. Het geordende paar (15, 62) komt overeen met een student van 15 jaar, anders dan het onwaarschijnlijke paar (62,15).

Het concept van een geordend koppel is erg belangrijk op verschillende wiskundegebieden, zoals het Cartesiaanse vlak, breuken, vectoren in het vlak, relaties en functies. Een belangrijk aspect is dat hun elementen niet noodzakelijkerwijs numeriek hebben, bijvoorbeeld, ze kunnen worden besteld met:

• Plattelandsstad
• Naam achternaam
• Vrouw echtgenoot

En vele andere combinaties.

Voorbeelden van geordende paren

Breuk

Een breuk wordt weergegeven als het quotiënt van twee P/Q -gehele getallen, bijvoorbeeld de fractie ½, die gelijkwaardig is aan het decimale nummer 0.5.

Deze fractie is echter niet de enige die het decimaal 0 vertegenwoordigt.5, ook het volgende:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2) ..

Op deze manier kan elke fractie worden weergegeven als een geordend paar (P, Q), waarbij P en Q heel zijn, waarbij P de positie van de teller bezet en Q die van de noemer. Er is een belangrijke beperking en dat Q (de noemer) anders moet zijn dan 0, omdat de fracties van de P/0 -vorm niet zijn gedefinieerd.

Kan u van dienst zijn: eindige set: eigenschappen, voorbeelden, opgeloste oefeningen

En een andere belangrijke voorwaarde is dat twee breuken A/B en C/D gelijk zijn zolang het wordt vervuld dat:

A ∙ D = B ∙ C

Functies en zijn grafieken

Een functie kan worden uitgedrukt als een set opgeruimde paren. Door bijvoorbeeld een functie in het Cartesiaanse vlak te grafieken, wordt het eerste element de positie van de onafhankelijke variabele toegewezen, terwijl de tweede de afhankelijke variabele wordt toegewezen. Dit is een geordend paar.

Voor de functie y = f (x) kan het nette koppel worden uitgedrukt als [x, f (x)]]. Overweeg bijvoorbeeld de startset:

A = 1, 2, 3, 4

In deze set zijn er de eerste componenten van een geordend paar volgens de Y = X -functie². De set van de tweede componenten is:

B = 1, 4, 9, 16

En de geordende paren worden gevormd zijn:

(1,1); (2,4); (3, 9); (4; 16)

Groet.

Vectoren in het vliegtuig

Vectoren kunnen in het Cartesiaanse vlak worden weergegeven door geordende paren, waarbij het eerste element de horizontale component "x" vertegenwoordigt en de tweede de verticale component "y". Om de vectoren te onderscheiden van de punten in het vlak, worden ze aangeduid met vetgedrukte letters en worden de vierkante haakjes gebruikt in plaats van de haakjes, zoals deze:

v =

Bijvoorbeeld de vector v = heeft een horizontale component gelijk aan 4 en verticale component gelijk aan 7. De grafiek is:

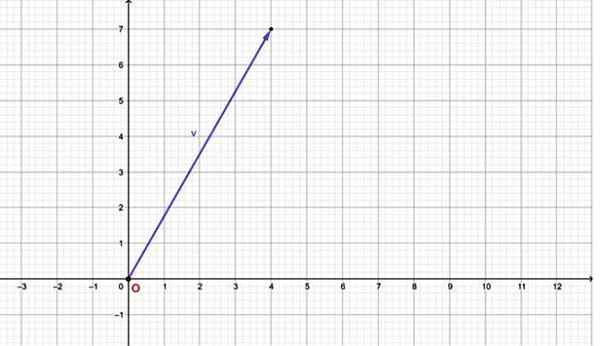Figuur 2.- Een vliegtuigvector kan worden uitgedrukt via een geordend paar. Bron: f. Zapata.

Merk op dat deze vector zijn oorsprong samenvalt met de oorsprong van het coördinatensysteem (0.0). Als de vector op elk ander punt zijn oorsprong heeft, kan deze ook worden uitgedrukt in de vorm van een geordend koppel via een ordelijke paren, om dit te doen, zie de volgende secties.

Kan u van dienst zijn: hiërarchie van operaties

Bestelde Pares -activiteiten

Toevoeging

Laat de doelen (a, b) en (c, d) paren zijn (d). Een nieuw koppel wordt verkregen door middel van zijn som volgens:

(a, b)+(c, d) = (a+c, b+d)

Neutraal element

Het neutrale element van de toevoeging van geordende paren is het koppel (0,0), omdat wanneer het bijdraagt ​​aan het geordende paar (a, b), de som is het laatste:

(a, b) + (0.0) = (a, b)

Som van het tegenovergestelde

Door een geordend paar (a, b) toe te voegen aan zijn tegenovergestelde (-a, -b) wordt het geordende koppel (0,0) verkregen:

(a, b) + (-a, -b) = (0.0)

Commutativiteit

De volgorde van de toevoegingen verandert de som niet:

(a, b) + (c, d) = (c, d) + (a, b)

Associativiteit

Het resultaat van het toevoegen van drie geordende paren wordt niet gewijzigd wanneer gegroepeerd om de bewerking uit te voeren:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Aftrekken van geordende paren

Laat de doelen (a, b) en (c, d) zijn, de aftrekking wordt als volgt uitgevoerd:

(A, B)-(C, D) = (A-C, B-D)

Product

In het product zijn er twee opties: i) vermenigvuldig een koppel dat wordt besteld door een constante en ii) vermenigvuldig twee (of meer) tuimelen.

Vermenigvuldiging door een constante

Laat K een constante en het geordende koppel (A, B) zijn, het product tussen de constante en het koppel is:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Vermenigvuldiging van geordende paren

Het product tussen de geordende paren (a, b) en (c, d) wordt als volgt uitgevoerd:

(A, B) X (C, D) = (AC - BD, BC+AD)

Neutraal element

Het neutrale element van vermenigvuldiging is (1.0), omdat door een koppel te vermenigvuldigen dat door dit is geordend, volgens de hierboven beschreven regel, het oorspronkelijke koppel is:

(a, b) x (1.0) = (a - 0, b + 0) = (a, b)

Kan u van dienst zijn: multiplicatief inverse: uitleg, voorbeelden, opgeloste oefeningen

Associativiteit

Aangezien de volgorde van de factoren het product niet verandert, kan het op verschillende manieren worden gegroepeerd om drie of meer nette paren te vermenigvuldigen en het resultaat is hetzelfde:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Opgeloste oefeningen

Oefening 1

Je hebt paren besteld (x², X-2) = (16, 2). Dat is de waarde van x?

Oplossing

Het toepassen van de gelijkheid van geordende paren wordt eerst verkregen:

X² = 16 ⇒ x₁ = 4, x₂ = -4

Om te weten welke van de twee waarden kiezen, gebruik van:

X-2 = 2

x = 2 + 2 = 4

Daarom is de gevraagde waarde van X 4.

Oefening 2

Express als een ordelijk paren de vector die van punt (1, 3) naar het punt (7, 11) gaat en deze grafisch weergeeft.

Oplossing

Zijn v De vector zocht. Om het geordende paar te bepalen dat het vertegenwoordigt, en dat zijn coördinaten bevat, worden de coördinaten van het aankomstpunt en het punt van oorsprong in die volgorde afgetrokken. Dus:

v = = =

De vector wordt vervolgens weergegeven v als degene die van (1.3) naar (7, 11) en de apparatuur gaat v waarvan de oorsprong is vastgesteld op de oorsprong van het coördinatensysteem (0.0). Zoals je kunt zien, hebben ze dezelfde richting en betekenis.

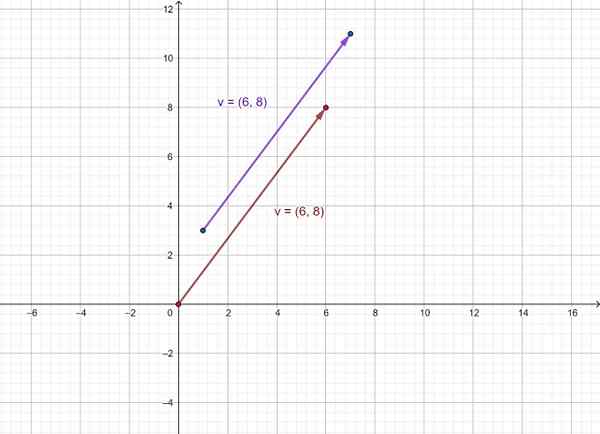figuur 3. Weergave van een vector als een ordelijk paar. Bron: f. Zapata.

Referenties

1. Diep. Besteld paar. Hersteld van: Deepai.borg.
2. Mathemovil. Cartesiaanse weergave van een vector door een geordend paar. Hersteld van: Matemovil.com.
3. Varsity tutorrs. Besteld paar. Opgehaald uit: WarsityTorm.com
4. Piestri, Juan. Relaties en functies. Faculteit Ingenieurswetenschappen. Afdeling Wiskunde. Buenos Aires 'University. Opgehaald uit: onderwerpen.fi.UBA.AR.
5. Universiteit van Denver. Relaties. Hersteld van: wiskunde.Ucdenver.Edu.