Papomudas

Wat is de papomudas?

Hij Papomudas Het is een procedure voor het oplossen van algebraïsche uitdrukkingen. Het acroniem geeft de volgorde van prioriteit van bewerkingen aan: haakjes, bevoegdheden, vermenigvuldiging, divisie, toevoeging en aftrekking. Met behulp van dit woord kunt u eenvoudig de volgorde onthouden waarin een uitdrukking uit verschillende bewerkingen moet worden opgelost.

Over het algemeen kunt u in numerieke uitdrukkingen verschillende rekenkundige bewerkingen samen vinden, zoals bedragen, aftrekking, vermenigvuldigingen en divisies, die ook fracties, krachten en wortels kunnen zijn. Om ze op te lossen, is het noodzakelijk om een ​​procedure te volgen die garandeert dat de resultaten correct zullen zijn.

Een rekenkundige uitdrukking die bestaat uit een combinatie van deze bewerkingen moet worden opgelost volgens de prioriteit van de orde, ook bekend als de hiërarchie van operaties, lang geleden opgericht in universele conventies. Aldus kunnen alle mensen dezelfde procedure volgen en hetzelfde resultaat verkrijgen.

Kenmerken

De Papomudas is een standaardprocedure die de volgorde vaststelt die moet worden gevolgd wanneer een uitdrukking moet worden gegeven, die is samengesteld uit een combinatie van bewerkingen zoals aftrekkingssom, vermenigvuldiging en verdeling.

Deze procedure bepaalt de volgorde van prioriteit van een bewerking met betrekking tot de anderen op het moment dat zij zullen zijn; dat wil zeggen, elke bewerking heeft een hiërarchische verschuiving of niveau om op te lossen.

De volgorde waarin de verschillende bewerkingen van een uitdrukking moeten worden opgelost, wordt gegeven door elk acroniem van het woord papomudas. Op deze manier moet je:

1. PA: haakjes, vierkante beugels of sleutels.
2. PO: Powers and Roots.
3. MU: vermenigvuldigingen.
4. D: Divisies.
5. A: toevoegingen of bedragen.
6. S: Aftrekkingen of aftrekking.

Deze procedure wordt ook in het Engels genoemd als PEMDAS; Om gemakkelijk te onthouden dat dit woord wordt geassocieerd met de uitdrukking: "Excuseer alstublieft mijn beste tante Sally”, Waarbij elke initiële letter overeenkomt met een rekenkundige bewerking, op dezelfde manier als de Papomudas.

Hoe ze op te lossen?

Gebaseerd op de hiërarchie die Papomudas heeft vastgesteld om de bewerkingen van een uitdrukking op te lossen, is het noodzakelijk om de volgende volgorde te vervullen:

• Ten eerste moeten alle bewerkingen die binnen de groeperingssymbolen zijn, zoals haakjes, sleutels, beugels en breukrepen worden opgelost. Wanneer er groepssymbolen binnen anderen zijn, moet u beginnen te berekenen van binnenuit.

Kan u van dienst zijn: kwadratische opvolgingen: voorbeelden, regel en oefeningen opgelost

Deze symbolen worden gebruikt om de volgorde te wijzigen waarin bewerkingen worden opgelost, omdat wat er altijd binnen is, altijd moet worden opgelost.

• Dan worden de krachten en wortels opgelost.
• Op de derde plaats worden vermenigvuldigingen en divisies opgelost. Deze hebben dezelfde volgorde van prioriteit; Daarom, wanneer deze twee bewerkingen in een uitdrukking worden gevonden, moet degene die eerst verschijnt, worden opgelost, waarbij de uitdrukking van links naar rechts wordt gelezen.
• Uiteindelijk worden de bedragen en aftrekken opgelost, die ook dezelfde volgorde van prioriteit hebben en daarom wordt het opgelost dat eerst in de uitdrukking verschijnt, van links naar rechts gelezen.
• Bewerkingen mogen nooit worden gemengd als u van links naar rechts wordt gelezen, moet u altijd de volgorde van prioriteit of hiërarchie volgen die door de Papomudas is vastgesteld.

Het is belangrijk om te onthouden dat het resultaat van elke bewerking in dezelfde volgorde moet worden geplaatst in relatie tot anderen, en alle tussenliggende stappen moeten worden gescheiden door een teken tot het bereiken van het eindresultaat.

Sollicitatie

Papomudas -procedure wordt gebruikt wanneer u een combinatie van verschillende bewerkingen hebt. Rekening houdend met hoe ze worden opgelost, kan dit worden toegepast in:

Uitdrukkingen die bedragen en aftrekkingen bevatten

Het is een van de eenvoudigste bewerkingen, omdat beide dezelfde volgorde van prioriteit hebben, zodat deze moet worden opgelost vanaf links naar rechts in de uitdrukking; Bijvoorbeeld:

22 -15 + 8 +6 = 21.

Uitdrukkingen die bedragen, aftrekking en vermenigvuldigingen bevatten

In dit geval is de werking van de hoogste prioriteit vermenigvuldiging, waarna de bedragen en aftrekken worden opgelost (degene die eerst in de uitdrukking is). Bijvoorbeeld:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24 -10 + 48 - 16 + 60

= 106.

Uitdrukkingen die som, aftrekvermenigvuldiging en divisie bevatten

In dit geval is er een combinatie van alle bewerkingen. Het begint met het oplossen van de vermenigvuldiging en verdeling met een superieure prioriteit, dan de bedragen en aftrekking. Het lezen van de uitdrukking van links naar rechts, deze wordt opgelost volgens zijn hiërarchie en positie binnen de uitdrukking; Bijvoorbeeld:

Kan je van dienst zijn: mumm

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Uitdrukkingen met som, aftrekking, vermenigvuldiging, verdeling en bevoegdheden

In dit geval is een van de getallen verhoogd tot een vermogen, die binnen het prioriteitsniveau eerst moet worden opgelost, en vervolgens vermenigvuldiging en divisies oplossen, en ten slotte de bedragen en de aftrekking:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

Net als de machten hebben de wortels ook de tweede orde van prioriteit; Daarom moeten ze in uitdrukkingen die ze bevatten, eerst worden opgelost dan vermenigvuldigingen, divisies, bedragen en aftrekken:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Uitdrukkingen die groeperingssymbolen gebruiken

Wanneer borden worden gebruikt zoals haakjes, sleutels, beugels en breuken, die hierin zijn, worden eerst opgelost, ongeacht de volgorde van prioriteit van de bewerkingen die het bevat met betrekking tot degenen die hierbuiten zijn, alsof het met een afzonderlijke uitdrukking:

14 ÷ 2 - (8 - 5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

Als er hierin verschillende bewerkingen zijn, moeten deze worden opgelost door hiërarchische volgorde. Vervolgens worden de andere bewerkingen die de uitdrukking vormen opgelost; Bijvoorbeeld:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

In sommige uitdrukkingen worden groeperingssymbolen binnen andere gebruikt, zoals wanneer het nodig is om het teken van een bewerking te wijzigen. In die gevallen moet het beginnen met het oplossen van binnenuit; dat wil zeggen, het vereenvoudigen van de groeperingssymbolen die zich in het midden van een uitdrukking bevinden.

Over het algemeen is de volgorde om bewerkingen in deze symbolen op te lossen: eerst oplossen wat tussen haakjes is (), vervolgens beugels [] en ten slotte de toetsen .

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Kan u van dienst zijn: theoretische waarschijnlijkheid: hoe u het uit kunt krijgen, voorbeelden, oefeningen

= 90 - 3 _* 24

= 90 - 72

= 18.

Opdrachten

Eerste oefening

Zoek de waarde van de volgende uitdrukking:

twintig² + √225 - 155 + 130.

Oplossing

Door de papomudas toe te passen, moeten de krachten en wortels eerst worden opgelost, en vervolgens toevoegen en aftrekken. In dit geval behoren de eerste twee bewerkingen tot dezelfde volgorde, dus degene die eerst is opgelost, beginnend van links naar rechts:

twintig² + √225 - 155 + 130

= 400 + 15 -155 + 130.

Voeg vervolgens toe en aftrekken, ook aan de linkerkant beginnen:

400 + 15 -155 + 130

= 390.

Tweede oefening

Zoek de waarde van de volgende uitdrukking:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Oplossing

Het begint met het oplossen van de bewerkingen die zich binnen de haakjes bevinden, volgens de hiërarchische volgorde die ze bezitten volgens de Papomudas.

Eerst worden de krachten van de eerste haakjes opgelost, waarna de bewerkingen van de tweede haakjes worden opgelost. Omdat ze tot dezelfde volgorde behoren, wordt de eerste bewerking van de uitdrukking opgelost:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216- 729) ÷ (8 _* 6 ÷ 16)]

= [ - (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Aangezien operaties binnen haakjes al zijn opgelost, wordt nu de divisie met de grootste hiërarchie voortgezet:

[- (-513) ÷ (3)] = [- (-171)]].

Ten slotte geeft de haakjes die het minus (-) -teken van het resultaat scheidt, dat in dit geval negatief is, aangeeft dat een vermenigvuldiging van deze tekenen moet worden gemaakt. Het resultaat van de uitdrukking is dus:

[- (-171)] = 171.

Derde oefening

Zoek de waarde van de volgende uitdrukking:

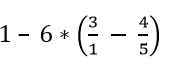
Oplossing

De breuken die zich binnen de haakjes bevinden, zijn opgelost:

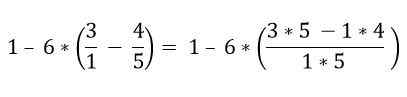
Binnen de haakjes zijn er verschillende bewerkingen. De vermenigvuldiging wordt eerst opgelost en vervolgens de aftrekkingen; In dit geval wordt de breukbalk beschouwd als een groeperingssymbool en niet als een divisie, dus de bewerkingen van het bovenste en onderste deel moeten worden opgelost:

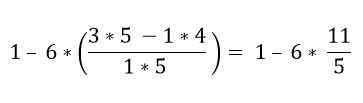
Bij hiërarchische volgorde moet vermenigvuldiging worden opgelost:

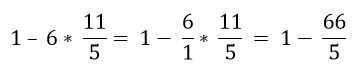
Ten slotte is de aftrekking opgelost: