Senoïde golfkenmerken, onderdelen, berekening, voorbeelden

De sinusgolven Het zijn golfpatronen die wiskundig kunnen worden beschreven door de sinus- en cosinusfuncties. Ze beschrijven terecht natuurlijke gebeurtenissen en variabele tekenen in de tijd, zoals spanningen gegenereerd door elektrische planten en vervolgens gebruikt in huizen, industrieën en straten.

Elektrische elementen zoals weerstanden, condensatoren en inductanties, die verbinden met sinusvormige spanningsingangen, produceren ook antwoorden ook sinusoïdaal. Wiskunde die in hun beschrijving worden gebruikt, zijn relatief eenvoudig en zijn grondig bestudeerd.

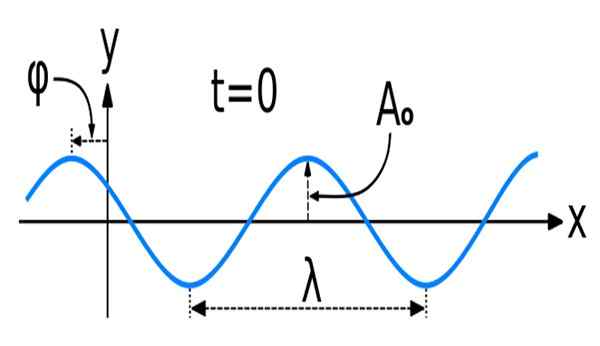
Figuur 1. Een sinusgolf met enkele van zijn belangrijkste ruimtelijke kenmerken: amplitude, golflengte en fase. Bron: Wikimedia Commons. Wave_new_sine.SVG: KraaiNestoriginally gemaakt als een cosinusgolf, door gebruiker: Pelegs, als bestand: Wave_New.Svgderivative Work: Dave3457 [CC BY-SA 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)]

De wiskunde van de sinusvormige of sinusvormige golven, zoals ze ook bekend zijn, is die van de sinus- en cosinusfuncties.

Dit zijn repetitieve functies, wat periodiciteit betekent. Beide hebben op dezelfde manier, met het voorbehoud dat de cosinus naar links is verplaatst ten opzichte van de borst in een fietsperruimte. Het wordt waargenomen in figuur 2:

Figuur 2. Sen X en Cos X -functies zijn ontheemd met betrekking tot de ander. Bron: f. Zapata.

Dan cos x = sin (x + π/2). Met behulp van deze functies wordt een sinusgolf weergegeven. Om dit te doen, wordt de grootte in kwestie op de verticale as geplaatst, terwijl in de horizontale as de tijd is gevonden.

De repetitieve kwaliteit van deze functies wordt ook op de bovenstaande grafiek gewaardeerd: het patroon wordt continu en regelmatig herhaald. Dankzij deze functies kunt u spanningen en stromen van het sinian -type in de loop van de tijd uitdrukken, waarbij u op de verticale as wordt geplaatst in plaats van de En, A v of een Je om spanning of stroom weer te geven, en op de horizontale as in plaats van de X, De T weer.

De meest algemene manier om een ​​sinusgolf uit te drukken is:

v (t) = v_M Sin (ωt+φ))

Dan zullen we de betekenis van deze uitdrukking verdiepen, wat enkele basisvoorwaarden definiëren om de sinusgolf te karakteriseren.

[TOC]

Partijen

Periode, amplitude, frequentie, cyclus en fase zijn concepten van toepassing op periodieke of repetitieve golven en zijn belangrijk om ze goed te karakteriseren.

Periode

Een periodieke functie zoals genoemde, die met regelmatige tussenpozen wordt herhaald, voldoet altijd aan de volgende eigenschap:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) =… .

Waar T Het is een bedrag dat wordt genoemd golf, En het is de tijd die nodig is om een ​​fase van hetzelfde te herhalen. In internationale systeemeenheden wordt de periode in seconden gemeten.

Amplitude

Volgens de algemene uitdrukking van de senoïde golf v (t) = v_M sin (ωt+φ), v_M Het is de maximale waarde van de functie, die optreedt wanneer sin (ωt+φ) = 1 (Onthouden dat de grootste waarde die de sinus- en cosinusfunctie beide toelaat, 1 is). Deze maximale waarde is precies de Golfamplitude, ook gekend als piekamplitude.

In het geval van een spanning wordt gemeten in volt en als het een stroom is, is deze in versterkers. In de sinusgolf is de breedte constant, maar in andere soorten golf kan de amplitude variëren.

Kan u van dienst zijn: Weerstandsthermometer: kenmerken, werking, gebruik

Fiets

Het is een deel van de golf in een periode. In de vorige figuur werd de periode genomen door deze te meten uit twee opeenvolgende pieken of richels, maar deze kan worden gemeten uit andere delen van de golf, terwijl ze worden beperkt door een periode.

Opmerking in de volgende figuur als de ene cyclus van het ene punt naar het andere bedekt met dezelfde waarde (hoogte) en dezelfde helling (helling).

figuur 3. In een sinusgolf vindt er altijd een cyclus plaats voor een periode. Het belangrijkste is dat het startpunt en het einde op dezelfde hoogte zijn. Bron: Boylestad. Inleiding tot circuitanalyse. Pearson.

Frequentie

Het is de hoeveelheid cycli die in 1 seconde plaatsvindt en is gekoppeld aan het argument van de sinusfunctie: ωt. De frequentie wordt aangeduid als F En het wordt gemeten in cycli per seconde of Hertz (Hz) in het internationale systeem.

De frequentie is daarom de omgekeerde hoeveelheid van de periode:

F = 1/t

Terwijl de frequentie F is gerelateerd aan de Hoekfrequentie ω (pulsatie) als:

Ω = 2πF

De hoekfrequentie wordt uitgedrukt in radianen /tweede in het internationale systeem, maar de radialen zijn dimensieloos, dus de frequentie F en hoekfrequentie Ω Ze hebben dezelfde dimensies. Merk op dat het product ωt geeft hierdoor radialen en moet rekening worden gehouden bij het gebruik van de rekenmachine om de waarde van te verkrijgen Sen ωt.

Fase

Het komt overeen met de horizontale verplaatsing die de golf ervaart, met betrekking tot een tijd die als referentie is genomen.

In de volgende figuur wordt de groene golf in een tijdstip naar voren gebracht ten opzichte van het rood T_D. Er zijn twee sinusvormige golven binnen fase Wanneer uw frequentie en fase hetzelfde zijn. Als de fase verschilt, zijn ze in gat. Figuur 2 golven zijn ook verouderd.

Figuur 4. Sinusidale golven pelied. Bron: Wikimedia Commons. Geen machine-leesbare auteur verstrekt. Kanjo ~ commonswiki veronderstelde (op basis van copyrightclaims). [Publiek domein].

Als de frequentie van de golven anders is, zijn ze in fase wanneer de fase ωt+φ Wees hetzelfde in beide golven op bepaalde momenten.

Senoidal Wave Generator

Er zijn veel manieren om een ​​sinusvormige signaal te verkrijgen. Zelfgemaakte looptjes bieden hen.

Toepassing van de wet van Faraday

Een vrij eenvoudige manier om een ​​sinussignaal te verkrijgen, is door de wet van Faraday te gebruiken. Dit geeft aan dat in een gesloten stroomcircuit, bijvoorbeeld een lus, geplaatst in het midden van een magnetisch veld, een geïnduceerde stroom wordt gegenereerd wanneer het magnetische veld erdoorheen stroomt. Bijgevolg a Geïnduceerde spanning of geïnduceerde FEM.

De stroom van het magnetische veld varieert als de lus wordt gedraaid met constante hoeksnelheid in het midden van het veld gecreëerd tussen de polen n en s van de in de figuur getoonde magneet.

Kan je van dienst zijn: Neptune (planeet)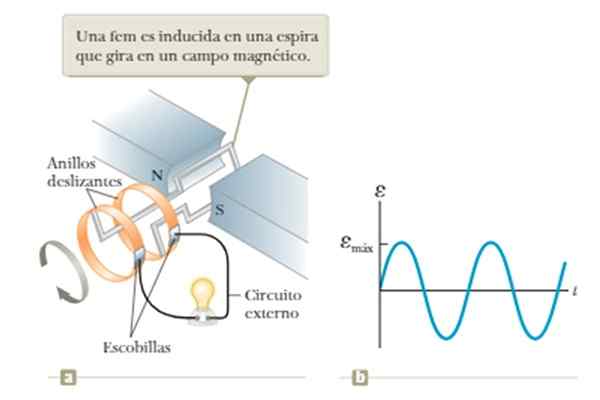Figuur 5. Golfgenerator op basis van de inductierecht van Faraday. Bron: Bron: Raymond A. Serway, Jonh W. Jewett [CC BY-SA 4.0 (https: // creativeCommons.Org/licenties/by-sa/4.0)].

De beperking van deze operatie is de afhankelijkheid van de spanning verkregen met de rotatiefrequentie van de lus, zoals in meer detail te zien is in voorbeeld 1 van de voorbeelden -sectie later.

Wien -oscillator

Een andere manier om een ​​sinusgolf te verkrijgen, dit keer met elektron. Op deze manier worden sinusgolven verkregen waarvan de frequentie en amplitude de gebruiker kan wijzigen op basis van hun gemak, door middel van schakelaanpassing.

De figuur toont een sinus -signaalgenerator, waarmee andere golfvormen ook kunnen worden verkregen: onder andere driehoekige en vierkanten.

Figuur 6. Een signaalgenerator. Bron: Bron: Wikimedia Commons. Opgrege bij Engelse Wikipedia [CC BY-SA 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)].

Hoe sinusgolven te berekenen?

Om berekeningen uit te voeren waarbij sinusgolven betrokken zijn, wordt een wetenschappelijke calculator gebruikt die de sinus- en cosinus -trigonometrische functies heeft, evenals zijn inverse. Deze rekenmachines hebben modi om de hoeken te werken, hetzij in graden of radianen, en het is gemakkelijk om de ene manier naar de andere te converteren. De conversiefactor is:

180 º = π Radianen.

Volgens het calculatiemodel moet u navigeren via de modus -toets om de optie op basis van de graad te vinden, waarmee u kunt werken aan trigonometrische functies in graden, of de RAD -optie, om de hoeken in radianen rechtstreeks te werken.

Bijvoorbeeld sin 25 º = 0.4226 met de calculator in de deg -modus. Door 25 º om te zetten in radianen krijg je 0.4363 radianen en sen 0.4363 rad = 0.425889 ≈ 0.4226.

De oscilloscoop

De oscilloscoop is een apparaat dat het mogelijk maakt om te visualiseren op een schermtekens van spanningen en stromen zowel afwisselend als direct. Het heeft knoppen om de grootte van het signaal op een rooster aan te passen zoals weergegeven in de volgende figuur:

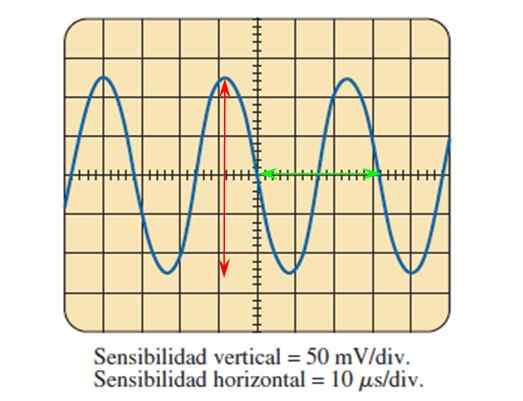Figuur 7. Een sinusvormig signaal gemeten met een oscilloscoop. Bron: Boylestad.

Door de afbeelding van de oscilloscoop en de aanpassing van de gevoeligheid in beide assen weten, is het mogelijk om de hierboven beschreven golfparameters te berekenen.

Kan u van dienst zijn: elliptische sterrenstelsels: vorming, kenmerken, typen, voorbeelden

De figuur toont het sinusspanningssignaal als een functie van de tijd, waarin elke verdeling van de verticale as 50 millivolt waard is, terwijl in de horizontale as elke divisie 10 microseconden waard is.

De piek naar piekamplitude is het tellen van de divisies die de golf verticaal omvat, helpt bij de rode pijl:

5 divisies worden geteld met behulp van de rode pijl, dus de piekpicospanning is:

V_PP = 5 divisies x 50 mV/divisie = 250 mV.

Spanning V_P Het wordt gemeten vanuit de horizontale as, die 125 mV is.

Om de periode te vinden die een cyclus wordt gemeten, bijvoorbeeld die van de groene pijl, die bedekt met 3.2 divisies, dan is de periode:

T = 3.2 divisies x 10 microseconden/divisie = 32 microseconden = 32 μs

Voorbeelden

voorbeeld 1

Voor de generator in figuur 3, demonstreer uit de wet van Faraday dat de geïnduceerde spanning sine heeft. Neem aan dat de lus bestaat uit N -bochten in plaats van één, allemaal met hetzelfde gebied A en draait met constante hoekige snelheid ω in het midden van een magnetisch veld B uniform.

Oplossing

De wet van Faraday zegt dat de geïnduceerde FEM ε is:

ε = -n (dφ_B /dt)

Waar Φ_B Het is de stroom van het magnetische veld, dat variabel zal zijn, omdat het afhangt van hoe de lus elk moment aan het veld wordt blootgesteld. Het negatieve teken beschrijft eenvoudig het feit dat deze FEM zich verzet tegen de oorzaak die het produceert (de wet van Lenz). De stroom als gevolg van een enkele lus is:

Φ_B = B.NAAR.Cos θ

θ is de hoek dat de normale vector ten opzichte van het vlak van de lus vormt met het veld B Terwijl de rotatie plaatsvindt (zie figuur), varieert deze hoek natuurlijk als:

θ = ωt

Zodat: Φ_B = B.NAAR.cos θ = b.NAAR.zomaar ωt. Nu moet je deze uitdrukking afleiden met betrekking tot tijd en daarmee wordt de geïnduceerde FEM verkregen:

ε = -n.D (B.NAAR.zomaar ωt) /dt

Zoals het veld B Het is uniform en het spasegebied varieert niet, ze verlaten de afgeleide:

ε = -nba. D (Cos ωt) /dt = ωnba. Sen ωt

Voorbeeld 2

Een lus heeft een oppervlakte van 0.100 m² en ga naar 60.0 Rev/s, met zijn rotatieas loodrecht op een uniform magnetisch veld van 0.200 t. Wetende dat de spoel 1000 beurten heeft om te vinden: a) de maximale FEM die wordt gegenereerd, b) de oriëntatie van de spoel in relatie tot het magnetische veld wanneer de maximaal geïnduceerde FEM optreedt.

Figuur 8. Een spiraal van N ronden gebroken in het midden van een uniform magnetisch veld en genereert een sinussignaal. Bron: r. Serway, Physics for Science and Engineering. Deel 2. Cengage leren.

Oplossing

a) de maximale FEM is ε_Maximaal = Ωnba

Voordat u de waarden vervangt, moet de frequentie van 60 Rev/s voor eenheden van het internationale systeem worden doorgegeven. Het is bekend dat 1 revolutie gelijk is aan een draai of 2p radianen:

60.0 Rev/s = 120p radianen/s

ε_Maximaal = 120p radianen x 1000 ronden x 0.200 t x 0.100 m² = 7539.82 V = 7.5 kV

b) Wanneer deze waarde optreedt Sen ωt = 1 daarom:

ωt = θ = 90º,

In dit geval is het spiraalvormige vlak evenwijdig aan B, Zodat de normale vector naar het genoemde vlak 90º vormt met het veld. Dit gebeurt wanneer de zwarte vector in figuur 8 loodrecht staat op de groene vector die het magnetische veld weergeeft.

Referenties

1. Boylestad, r. 2011. Inleiding tot circuitanalyse. 12e. Editie. Pearson. 327-376.
2. Figueroa, D. 2005. Elektromagnetisme. Fysieke serie voor wetenschap en engineering. Deel 6. Bewerkt door D. Figueroa. Simon Bolivar University. 115 en 244-245.
3. Figueroa, D. 2006. Fysica laboratorium 2. Redactionele equinox. 03-1 en 14-1.
4. Sinusgolven. Hersteld van: iessierradegara.com
5. Serway, r. 2008.Natuurkunde voor wetenschap en engineering. Deel 2. Cengage leren. 881-884