Oneven nummers

Wat zijn vreemde nummers?

De oneven nummers Het zijn die hele getallen die niet deelbaar zijn door 2. Dit betekent dat je met vreemde hoeveelheden geen groepen van een 2 kunt maken, bijvoorbeeld als iemand 9 snoepjes heeft om met een vriend te delen en er geen wil verdelen, zullen ze 4 snoepjes aanraken en de andere 5.

Sommige van de vreemde nummers zijn de volgende: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ..  In deze uitdrukking geven de suspensieve punten aan dat er meer getallen zijn, zowel links als rechts.

Afbeelding 1: Hoe te weten of een nummer vreemd is?

Zorgvuldig kijken, kunt u zien dat elk oneven nummer kan worden verkregen door 2 toe te voegen aan het voorgaande nummer. Als we bijvoorbeeld 2 aan -1 toevoegen, krijgt u 1, als we 1 + 2 maken, is dit 3 enzovoort.

Er wordt ook opgemerkt dat als de paren worden afgewisseld, inclusief 0, die als een even getal wordt beschouwd, de set hele getallen wordt verkregen Z.

Dat is de reden waarom elk oneven natuurlijk getal kan worden geschreven in de vorm 2n + 1, waarbij n = 0, ± 1, ± 2, ± 3, ± 4, ± 5 ..., waarbij het symbool ± betekent dat het als positief kan worden beschouwd of als negatief.

In het geval van grotere aantallen kan het worden herkend wanneer het een oneven is, omdat het altijd eindigt in 1, 3, 5, 7 of 9. 1571 is bijvoorbeeld vreemd en dat geldt ook voor het negatieve gehele Teger -152.489.

Voorbeelden van vreemde nummers

De vreemde cijfers worden vaak in de natuur gepresenteerd, en onder hen is het nummer 3 van speciale betekenis. Laten we eens kijken naar enkele voorbeelden:

-Er zijn veel bloemen met een oneven aantal bloemblaadjes.

-We hebben 5 vingers bij elke hand.

Kan u van dienst zijn: Willekeurige variabele: concept, typen, voorbeelden

-Mensen hebben 23 chromosomenparen.

-Er zijn de 3 wetten van Newton en de 3 wetten van de thermodynamica.

-De kernen van de atomen met een oneven aantal protonen en neutronen zijn minder stabiel dan die met een paarnummer.

-De wijzen zijn 3.

-In verhalen en verhalen verschijnt nummer 3 vaak, bijvoorbeeld romans zoals De drie Musketiers door Alejandro Dumas en in populaire verhalen zoals zoals De drie broers En De drie kleine biggetjes.

-Voor de artistieke compositie is er een oproep Vreemde regel, die vaststelt dat een compositie met een oneven aantal elementen aantrekkelijker is dan één met een paar. Het vreemde nummer voegt dynamiek toe, terwijl één paar stabiliteit biedt.

Figuur 2. Een oneven aantal elementen voegt dynamiek toe aan een afbeelding

-Een gemeenschappelijke strategie om objectprijzen goedkoper te laten lijken, is om 9 te eindigen, bijvoorbeeld 2.$ 99, $ 39 enzovoort.

-Het nummer 13 wordt door sommigen als pech als pech beschouwd, terwijl anderen mystieke kwaliteiten toeschrijven aan 11, beide vreemde nummers.

Primo -nummers

Primo -getallen, degenen die alleen als divisors zelf en 1 toelaten, zijn vreemd, met uitzondering van 2, wat het enige koppel van de neef is.

Het is mogelijk om aan te tonen dat elk getal kan worden afgebroken als een product van prime -factoren (inclusief deze krachten), en dat deze manier om het aantal uit te drukken uniek is, behalve in de volgorde van de factoren.

Nummer 45 kan bijvoorbeeld worden afgebroken als 45 = 3³ x 5.

Odd Numbers -bewerkingen

Met de vreemde cijfers worden alle rekenkundige bewerkingen uitgevoerd en sommige hebben uitstekende kenmerken.

Kan u van dienst zijn: symbolisatie van uitdrukkingen

- Sommen en producten

-De som van twee oneven getallen resulteert in een even getal: 3+5 = 8; 11+15 = 26; (-10)+ (+6) = - 4.

-Door een oneven getal met één koppel toe te voegen, is het resultaat oneven: 7+2 = 9; 26+ 9 = 35; (-5) + 12 = 7.

-Als de N eerste natuurlijke, vreemde en opeenvolgende nummers het resultaat is N². Laten we dit met een beetje meer detail bekijken:

Voor n = 2: 1 + 3 = 4 = 2²

Voor n = 3: 1 + 3 + 5 = 9 = 3²

Voor n = 4: 1 + 3 + 5 + 7 = 16 = 4²

-Wanneer een ODD wordt vermenigvuldigd met een paar, ontstaat een even nummer: 7 x 4 = 28; (-3) x 12 = -36.

-Twee oneven getallen vermenigvuldigen Een ODD wordt ook verkregen: 3 x 5 = 15; (-5) x (+11) = -55.

- Bevoegdheden

-Wanneer een positief getal wordt verhoogd tot een vreemde kracht, is het bijvoorbeeld een positief getal: 3³ = 27.

-Door een negatief getal naar een oneven vermogen te verhogen, is het resultaat negatief: (-2)³= (-2) x (-2) x (-2) = -8.

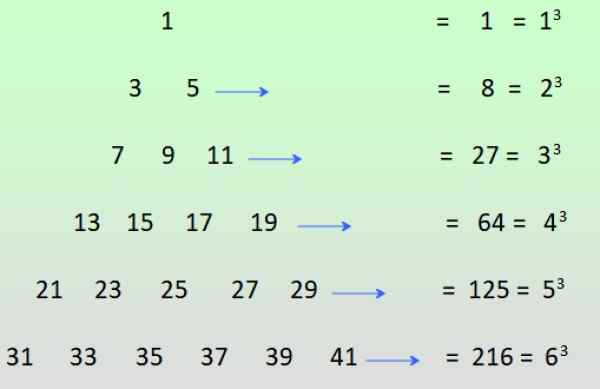
-Oneven krachten van positieve gehele getallen kunnen worden bereikt als er oneven getallen beschikbaar zijn zoals weergegeven in de figuur en de rijen worden toegevoegd:

figuur 3. Het verkrijgen van de vreemde bevoegdheden uit de som van vreemde getallen. Bron: f. Zapata.

Opgeloste oefeningen

- Oefening 1

Bepaal of het resultaat van de volgende bewerking gelijk of vreemd is:

(53476890083 + 1987628967) x 13567903

Oplossing

Om het antwoord te verkrijgen, hoeft u niet te draaien om een ​​rekenmachine te zoeken, maar om de geziene eigenschappen toe te passen. Laten we eens kijken naar de laatste cijfers van de Addends, die respectievelijk 3 en 7 zijn:

53476890083  + 1987628967

Dit betekent dat de verslaafden vreemd zijn en we weten al dat de som van twee vreemde nummers zelfs is.

Daarom is de figuur die het gevolg is van de haakjes zelfs en we zullen vermenigvuldigen met een nummer dat eindigt in 3:

Kan u van dienst zijn: vectoralgebra

13567903

Wat betekent dat dit nummer vreemd is.

In de hierboven beschreven eigenschappen werd vastgesteld dat het vermenigvuldigen van koppel X een even nummer is. Daarom is de resulterende bewerking zelfs.

- Oefening 2

Hoeveel is de som van de eerste 5 opeenvolgende oneven cijfers? En die van de eerste 50?

Oplossing

De som van de eerste 5 opeenvolgende oneven nummers is:

1 + 3 + 5 + 7 + 9 = 25

Maar als we de eerste 50 op deze manier willen toevoegen, is het omslachtig, dus we gaan naar de eigenschappen. Ze bevestigen dat de som van opeenvolgende vreemde nummers n is². In dit geval is n = 50 en de gevraagde som is:

vijftig² = 50 x 50 = 2500.

- Oefening 3

Wanneer drie opeenvolgende oneven nummers worden toegevoegd, wordt 237 verkregen. Wat zijn de cijfers?

Oplossing

Laten we ons eerste oneven nummer en de tweede en z naar de derde noemen, volgens de verklaring is het vervuld dat:

x + y + z = 237

In algebraïsche taal kan elk oneven nummer worden geschreven in de vorm 2n +1. Laten we ons eerste vreemde nummer maken:

x = 2n +1

Laten we 2 toevoegen om het volgende oneven te krijgen:

y = x + 2 = (2n + 1) + 2 = 2n + 3

En ten slotte wordt het opnieuw toegevoegd 2 om de derde oneven te verkrijgen:

Z = (2n +3) + 2 = 2n + 5

Dit alles voegt toe:

2n + 1 + 2n + 3 + 2n + 5 = 237

6n + 9 = 237

Dat resulteert in een eenvoudige lineaire vergelijking, waarvan de oplossing is:

n = 38

En nu met de waarde van n = 38 zijn er de drie bestellingen:

x = (2 × 38) + 1 = 77

Het volgende zijn daarom onvoldoende opeenvolgende:

y = 79

Z = 81

En de lezer kan gemakkelijk verifiëren dat de som van de drie 237 is.

Referenties

1. Baldor, een. 1986. Rekenkundig. Codex -edities en distributies.
2. Buurten, l. De vreemde cijfers en de krachten van natuurlijke getallen. Opgehaald uit: Sinewton.borg.
3. Briljant. Zelfs en vreemde nummers. Hersteld van: briljant.borg.
4. Wiskunde 18. Odd Numbers -bewerkingen. Opgehaald uit: Mathematics18.com.
5. Wikipedia. Zelfs en vreemde nummers. Hersteld van: is.Wikipedia.borg.