Hoeken en driehoeken
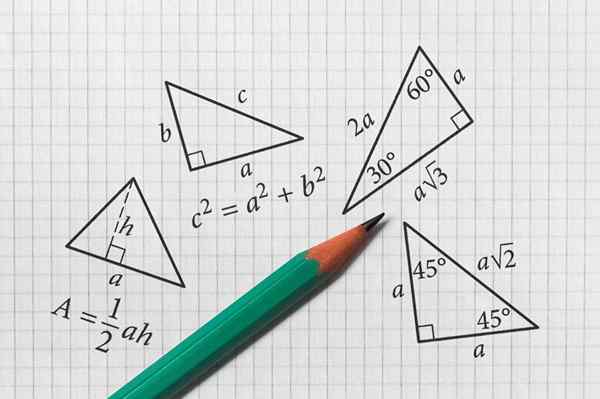
- 1576
- 356
- Kurt Aufderhar Jr.
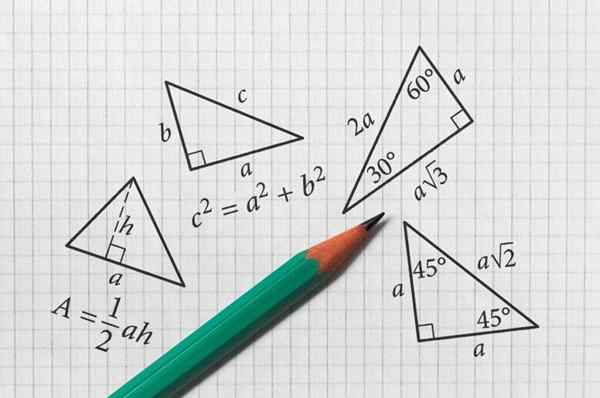 De hoeken en driehoeken maken deel uit van platte geometrie. Luiken
De hoeken en driehoeken maken deel uit van platte geometrie. Luiken Wat zijn hoeken en driehoeken?
A hoek Het is de regio van het vlak dat wordt afgebakend door twee semi -strak met een oogpunt in gemeenschappelijk. Dit punt staat bekend als de hoekpunt, Terwijl de semi -straight wordt genoemd zijkanten. Aan de andere kant, a driehoek Het is een figuur van drie hoeken en drie zijden, met drie hoekpunten.
We zullen eerst over de hoeken praten.
Hoeken
Er zijn verschillende manieren om de hoeken aan te duiden: door Griekse letters zoals α, β, γ, waaraan een circumflex -accent kan worden toegevoegd; met hoofdletters gestoffeerd of kleine letters, a, b, c, a, b, c; Nummers, zoals 1, 2, 3 ... of het gebruik van het hoeksymbool ∠.
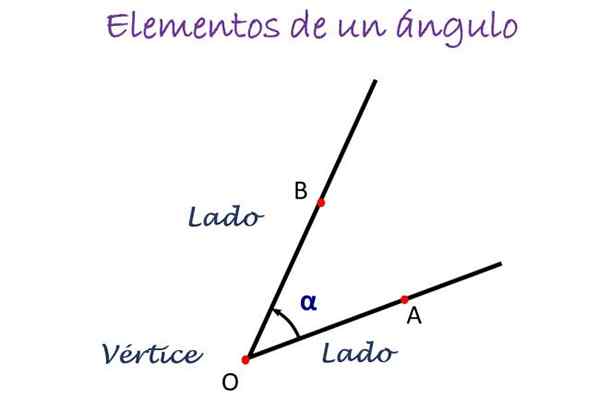 De belangrijkste elementen van een hoek. Bron: f. Zapata
De belangrijkste elementen van een hoek. Bron: f. Zapata In de bovenstaande figuur wordt de hoek gemeten vanaf zij A tot B, aangegeven door de richting van de pijl, en in het midden is de letter die het hoekpunt aangeeft, dat normaal of is. De hoek wordt vervolgens aangeduid als ∠ aob.
Wanneer de hoek wordt gemeten in een antihorarium -zin, wordt een +teken willekeurig toegewezen, en als deze in een schema wordt gemeten, moet u ze onderscheiden.
De maat van de hoeken wordt uitgevoerd door middel van een transporter, die bestaat uit een halfronde plastic plaat zoals die hieronder wordt getoond. De halve cirkel is verdeeld in 180 gelijke delen, elke oproep rang.
Om te meten, wordt het hoekpunt van de hoek samengevoegd met het centrale punt van de transporter, aangegeven met de pijl en de initiële kant met een van de randen, intern of extern. De laatste kant kruist enkele van de tekens van de transporter, deze maat is de hoek.
Kan u van dienst zijn: empirische regel: hoe u het toepast, waarvoor is het voor, opgeloste oefeningen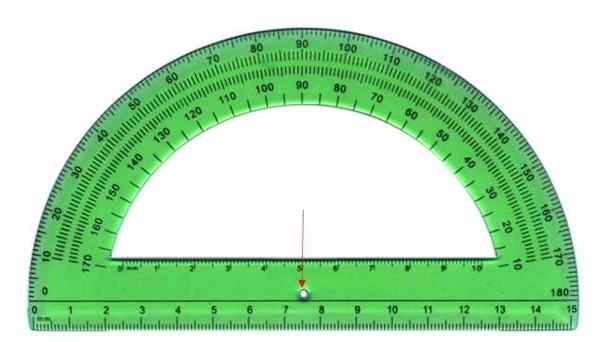 De transportband is het instrument om hoeken te meten. Bron: Wikimedia Commons
De transportband is het instrument om hoeken te meten. Bron: Wikimedia Commons Soorten hoeken
Een van de meest gebruikte criteria om hoeken te classificeren, is volgens de maatregel. Daarom kan een hoek zijn:
- Nul, Meet 0º.
- Scherp, wiens maat is tussen 0 en 90º.
- Direct, Het meet precies 90º.
- Stomp, Het is groter dan 90º en minder dan 180º.
- Vlak, De maatregel is gelijk aan 180º.
- Compleet, vertegenwoordigt een complete beurt en meet 360º.
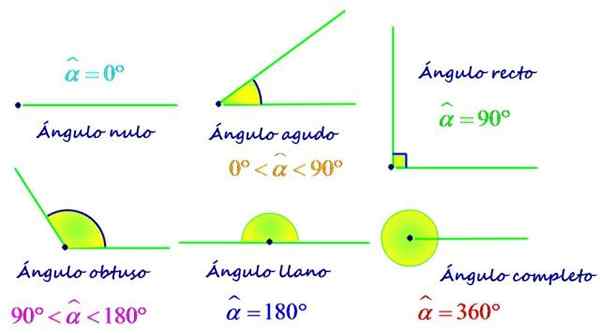 Soorten hoeken volgens uw maatregel. Bron: f. Zapata.
Soorten hoeken volgens uw maatregel. Bron: f. Zapata. Volgens de relatie tussen zijn maatregel en die van de vlakke hoek, die 180º is, kunnen de hoeken ook worden geclassificeerd als:
- Concaaf, Als het minder dan 180º meet. Daarom zijn de acute, rechte en stompe hoeken concaaf, omdat de maatregel altijd minder is dan 180º (zie de figuur hierboven).
- Convex, Als uw maat groter is dan 180º, als de hoeken van 270º en 360º.
Hoeken volgens de som van hun maatregelen en volgens de positie van hun zijden
Twee hoeken ∠ A en ∠ B kunnen zijn:
- Complementair, Als de som van zijn maatregelen gelijk is aan 90º.
- Aanvullend, Bij het toevoegen van de respectieve maatregelen wordt 180º verkregen.
- Geconjugeerd, Als deze som gelijk is aan 360º.
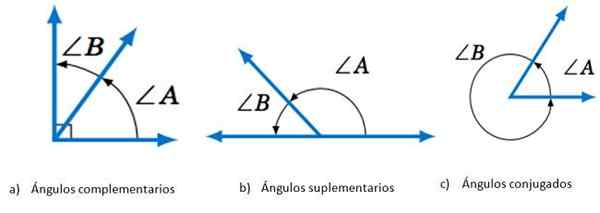 Hoeken volgens de som van zijn maatregelen. Bron: Wiskunde Librhethexts.
Hoeken volgens de som van zijn maatregelen. Bron: Wiskunde Librhethexts. Wat betreft de positie van hun zijden, twee hoeken kunnen zijn:
- In een rij, Wanneer het hoekpunt en een van de zijden gemeen hebben.
- Aangrenzend, Als ze opeenvolgend zijn, maar de niet -common -zijden zijn tegengesteld, dus ze zijn ook aanvullend.
- Tegenover het hoekpunt, Wanneer ze het gemeenschappelijke hoekpunt hebben en de zijkanten van de hoeken worden verlengd in de tegenovergestelde richting.
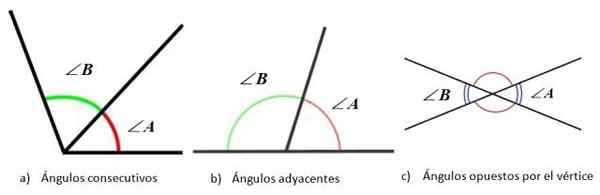 Hoeken volgens de relatieve positie tussen zijn zijkanten. Bron: f. Zapata
Hoeken volgens de relatieve positie tussen zijn zijkanten. Bron: f. Zapata Driehoeken
De driehoek is een platte en gesloten geometrische figuur, behorend tot de familie van de polygonen, met drie zijden bestaande uit lijnen die twee tot twee worden gesneden, waardoor drie hoeken worden gegenereerd.
Het kan u van dienst zijn: bijjectieve functie: wat is het, hoe wordt het gedaan, voorbeelden, oefeningenDe basiselementen zijn:
- Hoekpunten, die de snijpunten zijn van de bovengenoemde lijnen.
- Zijkanten, Een totaal van 3 en die bestaan uit de segmenten van lijnen die verbinding maken met de hoekpunten.
- Interne hoeken, Ook in getal van 3, waarvan de som altijd gelijk is aan 180º.
Over het algemeen worden de zijkanten aangeduid met kleine Latijnse letters, de hoekpunten met hoofdletters en de hoeken met kleine letters, maar andere notaties zijn ook mogelijk.
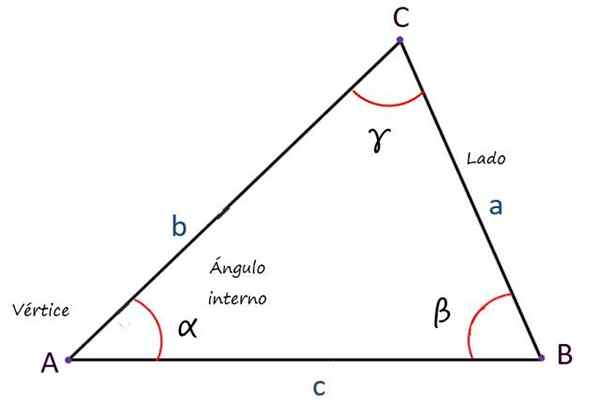 Hoofdelementen van een driehoek. Bron: f. Zapata
Hoofdelementen van een driehoek. Bron: f. Zapata Soorten driehoeken
Driehoeken volgens de vorm van zijn zijkanten
Volgens dit criterium kunnen driehoeken zijn:
- Equilaterals, Als de drie partijen dezelfde maatregel hebben.
- Gelijkbenig, Wanneer slechts twee van de zijkanten gelijke maatregelen hebben, terwijl de derde anders is.
- Scaleen, Als de drie zijden verschillende grootte hebben.
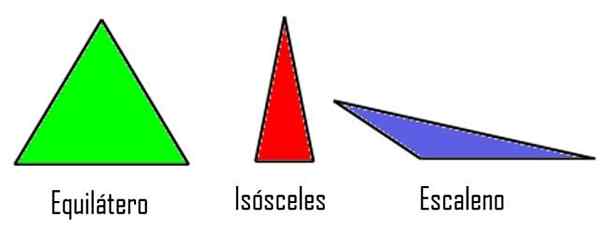 Driehoeken volgens hun kanten. Gemodificeerde Wikimedia Commons
Driehoeken volgens hun kanten. Gemodificeerde Wikimedia Commons Driehoeken volgens zijn interne hoeken
Dit criterium is gebaseerd op de interne hoektypen van de driehoek. Volgens dit kan een driehoek zijn:
- Verbinden, Wanneer de drie interne hoeken van de driehoek acuut zijn.
- Rechthoek, Als de driehoek een interne meethoek heeft die gelijk is aan 90º.
- Stomp, Een van de interne hoeken van de driehoek is stompe.
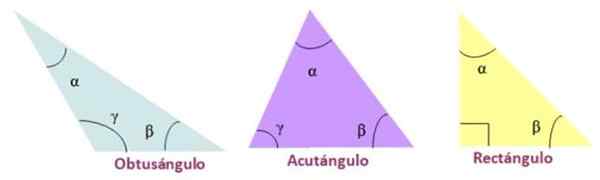 Soorten driehoek volgens zijn interne hoeken. Bron: f. Zapata
Soorten driehoek volgens zijn interne hoeken. Bron: f. Zapata Opmerkelijke driehoeksegmenten
Onder de opmerkelijke segmenten van een driehoek hebben ze:
- Mediaan, segment gericht vanuit een hoekpunt, rechtstreeks naar de andere kant.
- Middelares, Het is een segment dat behoort tot de lijn loodrecht op de zijkant, die kruist tot het middelpunt van die kant.
- Bissectrice, segment dat een interne hoek in twee gelijke delen verdeelt, en die zich uitstrekt tot de andere kant van de hoek.
- Hoogte, segment loodrecht op de zijkant, die zich uitstrekt tot het tegenovergestelde hoekpunt.
Drie medium, drie MediaTrices kunnen worden getraceerd enzovoort.
Driehoekscentra
In elke driehoek vallen de volgende punten op (zie de volgende figuur):
- Baricentro g, Ook soms wel genoemd zwaartepunt Van de driehoek is het het punt van snijpunt van de mediaan en is het altijd interieur van de driehoek.
- Ortocenter h, punt waarop de drie hoogten elkaar kruisen.
- Circumcentro of, Het is het punt van kruising van mediatrices. Het kan worden gevonden buiten de driehoek, als dit stompe is, terwijl, in de rechthoekige driehoek, of samenvalt met het middelpunt van de hypotenuse.
- In het midden, kruispunt voor driehoek bissectors.
- Euler recht, recht dat de baricenter verenigt, de orthocenter en de circumcentro, in elke driehoek die niet gelijkwaardig is. Het is altijd vervuld dat de lengte van het Hg -segment het dubbele is van het go -segment.
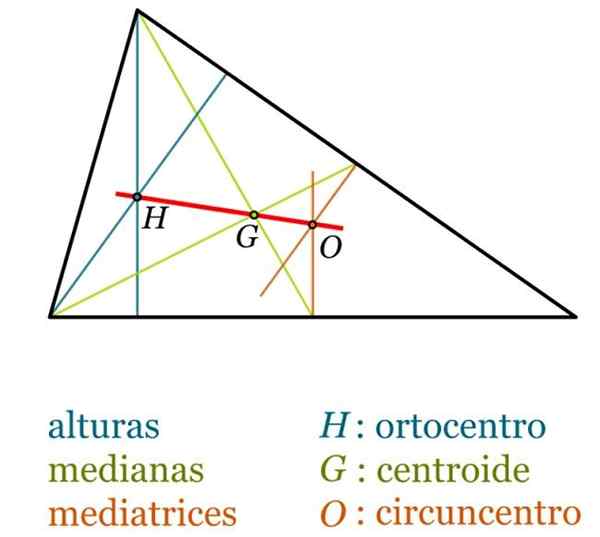 Opmerkelijke punten en segmenten van de driehoek. Bron: Wikimedia Commons
Opmerkelijke punten en segmenten van de driehoek. Bron: Wikimedia Commons Gebied van een driehoek
Om het gebied A van de driehoek te berekenen, wordt de volgende formule van algemene aard gebruikt:
A = basis × hoogte / 2
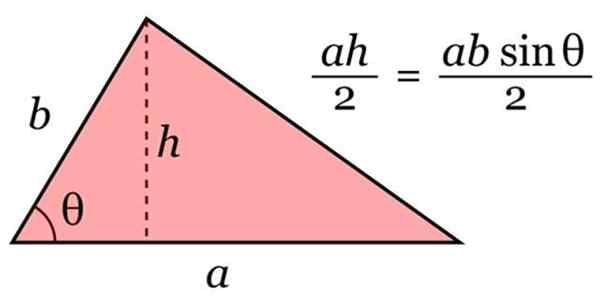 Gebied van de driehoek. Bron: Wikimedia Commons
Gebied van de driehoek. Bron: Wikimedia Commons Herón -formule
De lengte van alle kanten van de driehoek kennen, de volgende formule, bekend als Herón -formule, Hiermee kunt u gebied A vinden:
(s_p-b)(s_p-c))
Referenties
- Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
- Hoeken. Wiskunde Bibthetxts. Hersteld van: wiskunde.Librhetxts.borg.
- Jiménez, René. 2010. Wiskunde II (geometrie en trigonometrie). 2e. Editie. Pearson.
- Universe -formules. Driehoek. Hersteld van: UniversOFormulas.com.
- Zapata, f. Driehoeken: geschiedenis, elementen, classificatie, eigenschappen. Opgehaald uit: lifer.com.

