Externe alternatieve hoeken Oefeningen en oefeningen opgelost

De externe alternatieve hoeken Het zijn de hoeken die worden gevormd wanneer twee parallelle lijnen worden onderschept met een drooglijn. Naast deze hoeken wordt een ander koppel gevormd dat interne alternatieve hoeken wordt genoemd.

Het verschil tussen deze twee concepten zijn de "externe" en "interne" woorden en zoals de naam is aangegeven, de externe alternatieve hoeken zijn die die buiten de twee parallelle lijnen worden gevormd.

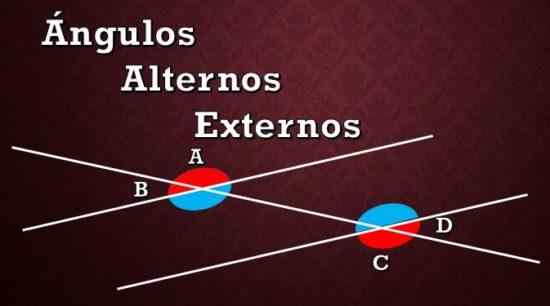
Grafische weergave van alternatieve externe hoeken A, B en C, D

Zoals te zien is in de vorige afbeelding, zijn er acht hoeken gevormd tussen de twee parallelle lijnen en de drooglijn. De rode hoeken zijn de externe alternatieve, en de blauwe hoeken zijn de interne alternatieve hoeken.

[TOC]

Kenmerken van externe alternatieve hoeken

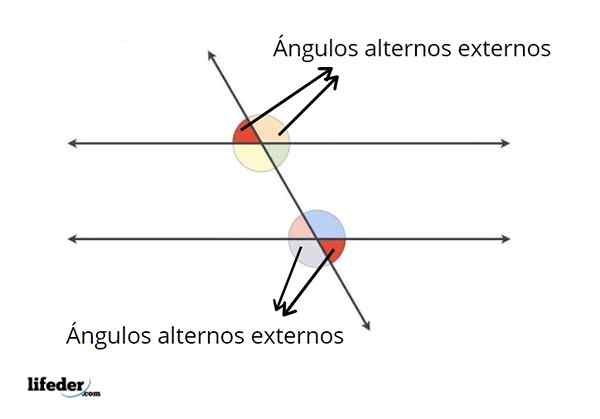Voorbeelden van externe alternatieve hoeken

In de inleiding werd al uitgelegd wat de externe alternatieve hoeken zijn. Naast het zijn van de externe hoeken tussen de parallellen, voldoen deze hoeken aan een andere voorwaarde.

De voorwaarde die ze voldoen, is dat de externe alternatieve hoeken die op een parallelle lijn worden gevormd congruent zijn; Het heeft dezelfde maat als de andere twee die op de andere parallelle lijn worden gevormd.

Maar elke externe alternatieve hoek is congruent met die aan de andere kant van de Secant -lijn.

Wat zijn de congruente externe alternatieve hoeken?

Als het beeld van het begin en de vorige verklaring wordt waargenomen, kan worden geconcludeerd dat de externe alternatieve hoeken die congruent zijn met elkaar zijn: hoeken A en C en hoeken B en D.

Om aan te tonen dat ze congruent zijn.

Kan u van dienst zijn: constante functie: kenmerken, voorbeelden, oefeningen

Opgeloste oefeningen

Hieronder staan ​​een reeks oefeningen waarbij de definitie en eigendom van congruentie van de externe alternatieve hoeken moet worden toegepast.

Eerste oefening

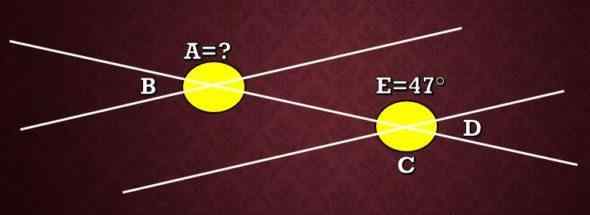
In het volgende beeld, wat is de maat voor hoek A weten dat de hoek E 47 ° meet?

Oplossing

Zoals eerder uitgelegd, zijn hoeken A en C congruent omdat ze extern alternatief zijn. Daarom is de maat van A gelijk aan de maat van C. Aangezien de hoeken E en C tegenover het hoekpunt staan, hebben ze dat ze dezelfde maatregel hebben, daarom is de maat van C 47 °.

Concluderend, de maat is gelijk aan 47 °.

Tweede oefening

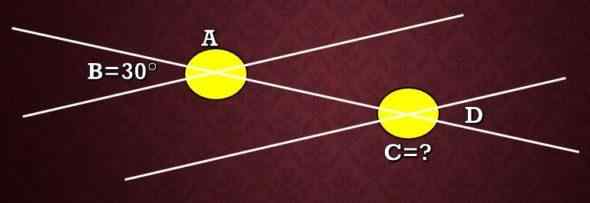
Bereken de maat van hoek C die wordt getoond in het volgende beeld, wetende dat hoek B 30 ° meet.

Oplossing

In dit voorbeeld wordt de definitie gebruikt. Twee hoeken zijn aanvullend als de som van hun maatregelen gelijk is aan 180 °.

In de afbeelding is te zien dat A en B aanvullend zijn, daarom a+b = 180 °, dat wil zeggen bij+30 ° = 180 ° en daarom a = 150 °. Nu zijn ze, net als A en C, externe alternatieve hoeken, dus de maatregelen zijn hetzelfde. Daarom is de C -maat 150 °.

Derde oefening

In de volgende afbeelding is de maat voor hoek A 145 °. Wat is de maat voor hoek e?

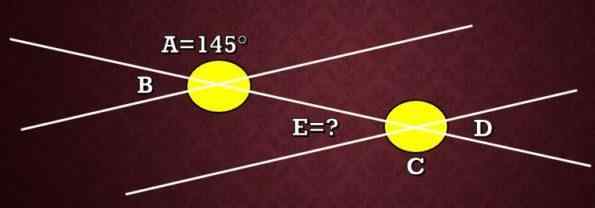
Oplossing

In de afbeelding is te zien dat hoeken A en C externe alternatieve hoeken zijn, daarom hebben ze dezelfde maatregel. Dat wil zeggen dat de maat van C 145 ° is.

Omdat hoeken C en E aanvullende hoeken zijn, moet het C+E = 180 ° zijn, dat wil zeggen 145 °+E = 180 ° en daarom is de maat voor hoek E 35 °.

Kan u van dienst zijn: bemonsteringsfout: formules en vergelijkingen, berekening, voorbeelden

Referenties

1. Bourke. (2007). Een invalshoek over geometrie wiskundewerkboek. NewPath Learning.
2. C. EN. NAAR. (2003). Geometrie -elementen: met talloze oefeningen en kompasgeometrie. Universiteit van Medellin.
3. Clemens, s. R., O'Dafer, p. G., & Cooney, t. J. (1998). Geometrie. Pearson Education.
4. Lang, s., & Murrow, g. (1988). Geometrie: een middelbare schoolcursus. Springer Science & Business Media.
5. Lira, a., Jaime, p., Chavez, m., Gallegos, m., & Rodríguez, c. (2006). Geometrie en trigonometrie. Umbrale edities.
6. Moyano, een. R., Saro, een. R., & Ruiz, r. M. (2007). Algebra en kwadratische geometrie. Netbiblo.
7. Palmer, c. Je., & Bibb, s. F. (1979). Praktische wiskunde: rekenkunde, algebra, geometrie, trigonometrie en berekeningsregel. Galm.
8. Sullivan, m. (1997). Trigonometrie en analytische geometrie. Pearson Education.
9. Wingard-Enelson, r. (2012). Geometrie. Enslow Publishers, Inc.