Rechthoekige componenten van een vector (met oefeningen)

De rechthoekige componenten van een vector zijn de gegevens waaruit deze vector bestaat. Om ze te bepalen, is het noodzakelijk om een ​​coördinatensysteem te hebben, meestal het Cartesiaanse vlak.

Zodra u een vector in een coördinatensysteem hebt, kunnen de componenten worden berekend. Dit zijn 2, een horizontale component (parallel aan de x -as), "component in de x -as" genoemd, en een verticale component (parallel aan de y -as), "component in de y -as" genoemd ".

Grafische weergave van de rechthoekige componenten van een vector

Om de componenten te bepalen, is het noodzakelijk.

[TOC]

Hoe de rechthoekige componenten van een vector te bepalen?

Om deze componenten te bepalen, moeten bepaalde relaties tussen rechthoeken en trigonometrische functies bekend zijn.

In de volgende afbeelding kunt u deze relatie zien.

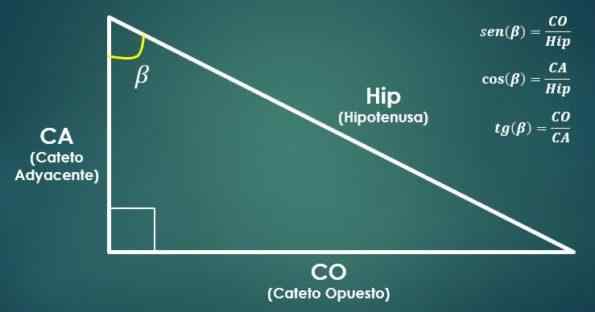Relaties tussen rechthoeken en trigonometrische functies

De boezem van een hoek is gelijk aan het quotiënt tussen de maat van de cateto die tegen de hoek is en de maat van de hypotenusa.

Aan de andere kant is de cosinus van een hoek gelijk aan het quotiënt tussen de maat van de cateto grenzend aan de hoek en de maat voor de hypotenusa.

De raaklijn van een hoek is gelijk aan het quotiënt tussen de maat van het tegenoverliggende been en de maat van de aangrenzende cateto.

In al deze relaties is het noodzakelijk om de bijbehorende rechthoekige driehoek vast te stellen.

Zijn er andere methoden?

Ja. Afhankelijk van de verstrekte gegevens, kan de manier om de rechthoekige componenten van een vector te berekenen, variëren. Een ander hulpmiddel dat veel wordt gebruikt, is Pythagoras Stelling.

Kan u van dienst zijn: bestaan ​​en uniekheid Stelling: demonstratie, voorbeelden en oefeningen

Opgeloste oefeningen

De volgende oefeningen brengen de definitie van de rechthoekige componenten van een vector en de hierboven beschreven relaties in praktijk.

Eerste oefening

Het is bekend dat een vector A een grootte heeft gelijk aan 12 en de hoek die deze vorm met de X -as heeft een maatregel van 30 ° heeft. Bepaal de rechthoekige componenten van genoemde vector tot.

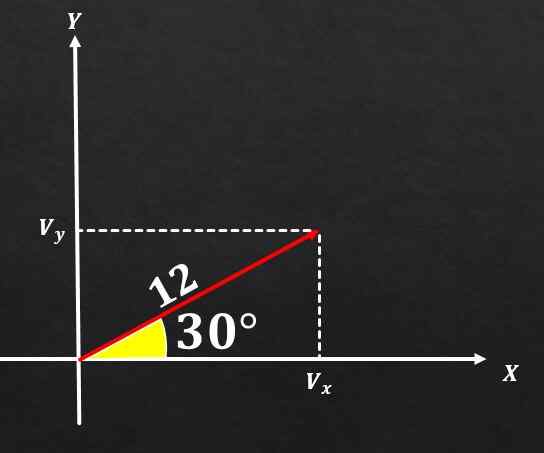
Oplossing

Als de afbeelding wordt gewaardeerd en de hierboven beschreven formules worden gebruikt, kan worden geconcludeerd dat de component in de en vector A gelijk is aan

sin (30 °) = vy / 12, en daarom vy = 12*(1/2) = 6.

Aan de andere kant is de component op de x -as van vector A gelijk aan

cos (30 °) = vx / 12, en daarom vx = 12*(√3 / 2) = 6√3.

Tweede oefening

Als vector A een grootte heeft die gelijk is aan 5 en de component op de X -as gelijk is aan 4, bepaal dan de waarde van de A -component op de Y -as.

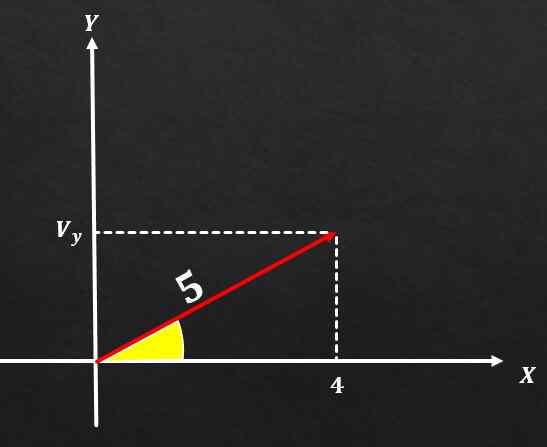
Oplossing

Met behulp van de Pythagoras -stelling moet de grootte van de vector een hoge vierkante gelijkenis gelijk zijn aan de som van de vierkanten van de twee rechthoekige componenten. Dat wil zeggen, m² = (vx) ² + (vy) ².

Het vervangen van de verstrekte waarden moet u

5² = (4) ² + (vy) ², daarom, 25 = 16 + (vy) ².

Dit houdt in dat (vy) ² = 9 en bijgevolg vy = 3.

Derde oefening

Als vector A een grootte heeft die gelijk is aan 4 en deze vormt een hoek van 45 ° met de X -as, bepaal dan de rechthoekige componenten van genoemde vector.

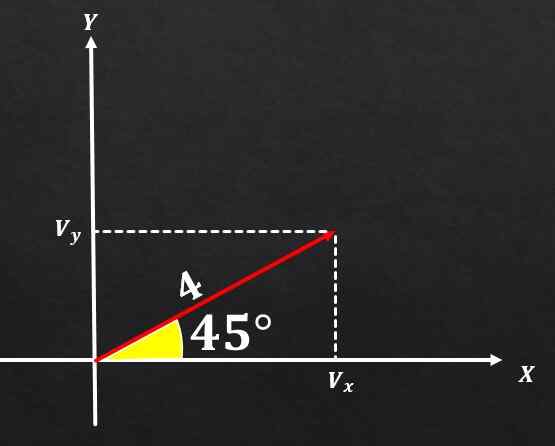
Oplossing

Met behulp van de relaties tussen een rechthoekige driehoek en trigonometrische functies kan worden geconcludeerd dat de component op de en vector A gelijk is aan

sin (45 °) = vy / 4, en daarom vy = 4*(√2 / 2) = 2√2.

Aan de andere kant is de component op de x -as van vector A gelijk aan

Kan u van dienst zijn: samengestelde opvolging

cos (45 °) = vx / 4, en daarom vx = 4*(√2 / 2) = 2√2.

Referenties

1. Landaverde, f. D. (1997). Geometrie (Herdruked ed.)). Voortgang.
2. Leake, D. (2006). Driehoeken (Geïllustreerd ED.)). Heinemann-RaTree.
3. Pérez, c. D. (2006). Voorzetting. Pearson Education.
4. Ruiz, á., & Barrantes, h. (2006). Geometrieën. CR Technological.
5. Sullivan, m. (1997). Voorzetting. Pearson Education.
6. Sullivan, m. (1997). Trigonometrie en analytische geometrie. Pearson Education.