Willekeurige steekproefmethode, voor-, nadelen, voorbeelden

Hij Willekeurige steekproeven Het is de manier om een ​​statistisch representatieve steekproef te selecteren uit een bepaalde populatie. Een deel van het principe dat elk element van het monster dezelfde kans moet hebben om te worden geselecteerd.

Een loterij is een voorbeeld van willekeurige steekproef, waarin elk lid van de populatie deelnemers een nummer krijgt. Om de nummers te kiezen die overeenkomen met de Raffle Awards (het monster) wordt een willekeurige techniek gebruikt, bijvoorbeeld extract uit een mailbox de nummers die werden gescoord op identieke kaarten.

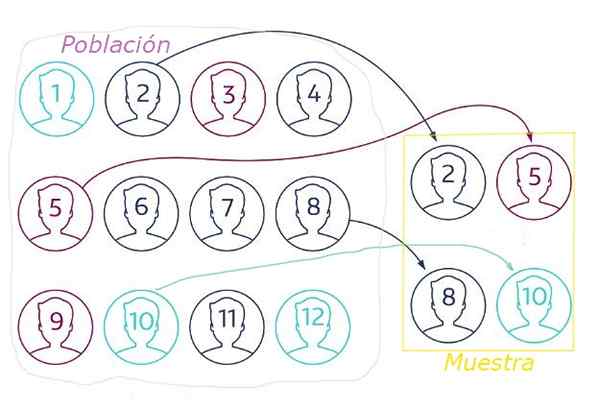Figuur 1. In willekeurige bemonstering wordt de steekproef geëxtraheerd uit willekeurige populatie door een techniek die ervoor zorgt dat alle elementen dezelfde kans hebben om te worden gekozen. Bron: Netquest.com.

In willekeurige bemonstering is het essentieel.

[TOC]

De grootte van het monster

Er zijn formules om de juiste grootte van een monster te bepalen. De belangrijkste factor om te overwegen is of de populatiegrootte bekend is. Laten we eens kijken naar de formules om de steekproefgrootte te bepalen:

Case 1: Populatiegrootte is niet bekend

Wanneer de grootte van de populatie onbekend is, is het mogelijk om een ​​adequate N -steekproef te selecteren, om te bepalen of een bepaalde hypothese waar of onwaar is.

Hiervoor wordt de volgende formule gebruikt:

n = (z² P Q)/(E²))

Waar:

-P Het is de kans dat de hypothese waar is.

-Q is de kans dat het dat niet is, daarom q = 1 - p.

-E is de relatieve foutmarge, bijvoorbeeld een fout van 5% heeft een marge E = 0,05. 

-Z heeft te maken met het niveau van vertrouwen dat de studie vereist.

Kan u van dienst zijn: normale verdeling: formule, kenmerken, bijvoorbeeld oefening

In een normale verdeling getypeerd (of genormaliseerd) heeft een betrouwbaarheidsniveau van 90% z = 1.645, omdat de kans dat het resultaat ligt tussen -1,645σ en +1.645σ is 90%, waarbij σ de standaardafwijking is.

Vertrouwensniveaus en hun bijbehorende Z -waarden 

1.- 50% betrouwbaarheidsniveau komt overeen met z = 0,675.

2.- 68.3% betrouwbaarheidsniveau komt overeen met z = 1.

3.- 90% betrouwbaarheidsniveau gelijkwaardig aan z = 1.645.

4.- 95% betrouwbaarheidsniveau komt overeen met z = 1,96

5.- 95,5% betrouwbaarheidsniveau komt overeen met z = 2.

6.- 99,7% betrouwbaarheidsniveau is gelijk aan z = 3.

Een voorbeeld waarin deze formule kan worden toegepast, zou in een onderzoek zijn om het gemiddelde gewicht van de kiezelstenen van een strand te bepalen.

Het is duidelijk niet mogelijk om alle kiezelstenen van het strand te bestuderen en af ​​te wegen, dus het is handig.

Figuur 2. Om de kenmerken van de kiezelstenen van een strand te bestuderen, is het noodzakelijk om een ​​willekeurig monster te kiezen met een representatief nummer van hen. (Bron: Pixabay)

Case 2: Populatiegrootte is bekend

Wanneer het aantal n van elementen waaruit een bepaalde populatie bestaat (of universum) bekend is, als u wilt selecteren door eenvoudige willekeurige steekproef een statistisch significante steekproefmonster, is dit de formule: 

n = (z²p q n)/(n e² + Z²P Q)

Waar:

-Z is de coëfficiënt geassocieerd met het vertrouwensniveau.

-P is de kans op succes van de hypothese.

-Q is de kans op falen in de hypothese, p + q = 1.

-N is de grootte van de totale bevolking.

-E is de relatieve fout van het onderzoeksresultaat.

Voorbeelden

De methode om de monsters te extraheren hangt veel af van het type onderzoek dat nodig is om te doen. Daarom heeft willekeurige bemonstering talloze toepassingen:

Kan u van dienst zijn: tekenen van groepering

Enquêtes en vragenlijsten

In telefonische enquêtes worden bijvoorbeeld mensen gekozen om te worden geraadpleegd door een willekeurige getallengenerator, van toepassing op de regio die wordt onderzocht.

Als u een vragenlijst wilt toepassen op de werknemers van een groot bedrijf, kan de selectie van respondenten worden gebruikt via hun werknemersnummer of identiteitskaartnummer.

Dit nummer moet ook willekeurig worden gekozen, bijvoorbeeld met behulp van een willekeurige nummergenerator.

figuur 3. Een vragenlijst kan willekeurig worden toegepast om deelnemers te selecteren. Bron: Pixabay.

QA

In het geval dat de studie op de door een machine wordt vervaardigd, moeten onderdelen willekeurig worden gekozen, maar van kavels gemaakt op verschillende tijdstippen van de dag, of in verschillende dagen of weken.

Voordelen

Eenvoudige willekeurige bemonstering:

- Het maakt het mogelijk om de kosten van een statistisch onderzoek te verlagen, omdat het niet nodig is om de totale populatie te bestuderen om statistisch betrouwbare resultaten te verkrijgen, met de gewenste niveaus van vertrouwen en het foutenniveau dat in de studie vereist is.

- Vermijd vooringenomenheid: omdat de keuze van de te bestuderen elementen volledig willekeurig is, weerspiegelt de studie trouw de kenmerken van de populatie, hoewel slechts een deel van hetzelfde werd bestudeerd.

Nadelen

- De methode is niet toereikend in gevallen dat u de voorkeuren in verschillende groepen of populatielagen wilt weten.

In dit geval verdient het de voorkeur om eerder de groepen of segmenten te bepalen waarop de studie is gedaan. Zodra de lagen of groepen zijn gedefinieerd, als het voor elk van hen handig is om willekeurige steekproeven toe te passen.

- Het is zeer onwaarschijnlijk dat informatie over de minderheidssectoren wordt verkregen, waarvan het soms nodig is om hun kenmerken te kennen.

Kan u van dienst zijn: Simpson Regel: formule, demonstratie, voorbeelden, oefeningen

Als het bijvoorbeeld een campagne is voor een duur product, is het noodzakelijk om de voorkeuren van de rijkste minderheidssectoren te kennen.

Oefening opgelost

We willen de voorkeur van de bevolking bestuderen door de manier van Cola van Cola, maar er is geen eerdere studie in die populatie, waarvan de grootte onbekend is.

Aan de andere kant moet het monster representatief zijn met een minimaal betrouwbaarheidsniveau van 90% en de conclusies moeten een procentuele fout van 2% hebben.

-Hoe de S -grootte van het monster te bepalen?

-Wat zou de steekproefomvang zijn als de foutmarge tot 5% is gemaakt?

Oplossing

Omdat de populatiegrootte onbekend is, wordt de hierboven gegeven formule gebruikt om de grootte van de steekproef te bepalen:

n = (z²P Q)/(E²))

We gaan ervan uit dat er dezelfde kans op voorkeur is (P) door onze verfrissing die van niet -preferentie (Q), dan p = q = 0,5.

Aan de andere kant, omdat het onderzoeksresultaat een procentuele fout moet hebben, minder dan 2%, dan is de relatieve fout 0,02.

Ten slotte produceert een waarde z = 1.645 een betrouwbaarheidsniveau van 90%.

Kortom, je hebt de volgende waarden:

Z = 1.645

P = 0,5

Q = 0,5

E = 0,02

Met deze gegevens wordt de minimale steekproefgrootte berekend:

N = (1.645² 0,5 0,5)/(0,02²) = 1691.3

Dit betekent dat de studie met de vereiste foutenmarge en met het gekozen vertrouwensniveau een steekproef van respondenten van ten minste 1692 personen moet hebben, gekozen door eenvoudige willekeurige bemonstering.

Als u van een foutmarge gaat van 2% tot 5%, dan is de nieuwe steekproefgrootte:

N = (1.645² 0,5 0,5)/(0,05²) = 271

Dat is een aanzienlijk lager aantal individuen. Concluderend is de steekproefgrootte zeer gevoelig voor de gewenste marge in de studie.

Referenties

1. Berenson, m. 1985.Statistieken voor administratie en economie, concepten en toepassingen. Inter -Amerikaans redactioneel.
2. Statistieken. Willekeurige steekproeven. Uitgebracht van: Encyclopediaeconomica.com.
3. Statistieken. Bemonstering. Hersteld van: statistieken.Mat.Ons op.mx.
4. Verkennenbaar. Willekeurige steekproeven. Hersteld van: Exploreerbaar.com.
5. Moore, D. 2005. Basisstatistieken toegepast. 2e. Editie.
6. Netquest. Willekeurige steekproeven. Hersteld van: Netquest.com.
7. Wikipedia. Statistische steekproef. Opgehaald uit: in.Wikipedia.borg